2024年北师大版数学八（下）微素养核心突破1 等腰三角形中...

更新时间：2024-04-16 浏览次数：232 类型：复习试卷

一、选择题

1. (2024八上·北海期末) 已知一个等腰三角形的两边长分别为 $\text{[math]}$ 和 $\text{[math]}$ ，则它的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·中江期中) 如图，为了让电线杆垂直于地面，工程人员的操作方法通常是：从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC ，当固定点B ， C到杆脚E的距离相等，且B ， E ， C在同一直线上时，电线杆DE就垂直于BC ．工程人员这种操作方法的依据是（　　）

A . 等边对等角 B . 等腰三角形“三线合一” C . 垂线段最短 D . 线段垂直平分线上的点到这条线段两端点的距离相等

答案解析收藏纠错 + 选题
3. (2023八上·广州期末) 如图，在 $\text{[math]}$ 的正方形网格中有两个格点A、B ，连接AB ，在网格中再找一个格点C ，使得 $\text{[math]}$ 是等腰三角形，满足条件的格点C的个数是（）

A . 5 B . 6 C . 8 D . 9

答案解析收藏纠错 + 选题
4. (2023七下·花溪月考) 已知等腰三角形的两边长分别为6和2，则这个三角形的周长是（）

A . 14 B . 10 C . 14或10 D . 12

答案解析收藏纠错 + 选题
5. (2024八上·黄石港期末) 如图， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 方格纸中格点上的两点，若以 $\text{[math]}$ 为边，在方格中取一点 $\text{[math]}$ （ $\text{[math]}$ 在格点上），使得 $\text{[math]}$ 为等腰三角形，则点 $\text{[math]}$ 的个数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·高邑期末) 已知一个等腰三角形两内角的度数之比为 $\text{[math]}$ ： $\text{[math]}$ ，则这个等腰三角形的底角的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八上·鄂州期末) 已知等腰 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 边上的垂直平分线与直线 $\text{[math]}$ 所夹的锐角为 $\text{[math]}$ ，则等腰 $\text{[math]}$ 顶角的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024八下·高州月考) 如图所示，点A坐标为(-3，0) 点B坐标为(1，4)，在y轴上存在一点C，使得△ABC为等腰三角形，则满足此条件的点C最多有（）

A . 4个 B . 5个 C . 6个 D . 8个

答案解析收藏纠错 + 选题

二、填空题

9. (2023八上·杭州月考) 若等腰△ABC的两条边长为6cm和2cm，则等腰三角形周长为cm．

答案解析收藏纠错 + 选题
10. (2024八上·赣州期末) 如图，B是射线 $\text{[math]}$ 上动点， $\text{[math]}$ ，若 $\text{[math]}$ 为等腰三角形，则 $\text{[math]}$ 的度数可能是．

答案解析收藏纠错 + 选题
11. (2024八上·雨湖期末) 用一条24cm的细绳围成一个等腰三角形，若其中有一边的长为6cm，则该等腰三角形的腰长为．

答案解析收藏纠错 + 选题
12. (2024八上·拱墅期末) 如图，已知在Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别在边 $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，翻折后，点B，C分别落在点 $\text{[math]}$ ， $\text{[math]}$ 处，且边 $\text{[math]}$ 与 $\text{[math]}$ 在同一条直线上，连接 $\text{[math]}$ ，当△ADC’是以 $\text{[math]}$ 为腰的等腰三角形时，则BD=．

答案解析收藏纠错 + 选题
13. (2023八上·德惠月考) 如图，在△ABC中，AB＝AC ， ∠B＝40°，点D在线段BC上运动（D不与B、C重合），连接AD ，作∠ADE＝40°，DE交线段AC于E ，在点D的运动过程中，△ADE的形状也在改变，当△ADE是等腰三角形时，∠BDA的度数是．

答案解析收藏纠错 + 选题
14. (2024八上·嘉兴期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，点D是 $\text{[math]}$ 上一动点，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠得到 $\text{[math]}$ ，当 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分是直角三角形时， $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
15. (2024八上·汉阳期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ；点D在 $\text{[math]}$ 边上，将 $\text{[math]}$ 沿 $\text{[math]}$ 所在直线翻折得 $\text{[math]}$ 、 $\text{[math]}$ 角平分线交 $\text{[math]}$ 边于点G，连接 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ 为等腰三角形，则θ的值．

答案解析收藏纠错 + 选题

三、解答题

16. (2019七下·醴陵期末) 阅读材料：我们知道：若几个非负数相加得零，则这些数都必同时为零。
例如：①（a﹣1）²+（b+5）²=0，我们可以得：（a﹣1）²=0，（b+5）²=0，∴a=1，b=-5．

②若m²-4m+n²+6n+13=0，求m、n的值．

解：∵m²-4m+n²+6n+13=0，

∴（m²﹣4m+4)+(n²+6n+9)=0(我们将13拆成4和9，等式左边就出现了两个完全平方式）

∴(m﹣2)²+(n+3)²=0，

∴(m﹣2)²=0，(n+3)²=0，

∴ n=2，m=-3．

根据你的观察，探究下面的问题：
1. （1） a²﹣4a+4+b²=0，则a=．b=．
2. （2）已知x²+2xy+2y²－6y+9=0，求x^y的值．
3. （3）已知a、b（a≠b）是等腰三角形的边长，且满足2a²+b²﹣8a﹣6b+17=0，求三角形的周长。
答案解析收藏纠错 + 选题
17. (2023八上·潮南期末) 如图，已知：在△ABC中，AC=BC=8，∠ACB=120°，将一块足够大的直角三角尺PMN（∠M=90°，∠MPN=30°）按如图放置，顶点P在线段AB上滑动，三角尺的直角边PM始终经过点C，并且与CB的夹角∠PCB=α，斜边PN交AC于点D．
1. （1）当PN∥BC时，判断△ACP的形状，并说明理由；
2. （2）点P在滑动时，当AP长为多少时，△ADP与△BPC全等，并说明理由；
3. （3）点P在滑动时，△PCD的形状可以是等腰三角形吗？若可以，
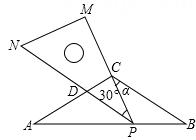
  请直接写出夹角α的大小；若不可以，请说明理由．
答案解析收藏纠错 + 选题
18. (2024八上·郫都期末) 对于平面直角坐标系 $\text{[math]}$ 中的点 $\text{[math]}$ 、 $\text{[math]}$ ，给出如下定义：若 $\text{[math]}$ 、 $\text{[math]}$ 为某个三角形的顶点，且边 $\text{[math]}$ 上的高 $\text{[math]}$ ，满足 $\text{[math]}$ ，则称该三角形为点 $\text{[math]}$ 、 $\text{[math]}$ 的“等值三角形”，已知点 $\text{[math]}$ ．
1. （1）若点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的正半轴上，且 $\text{[math]}$ 是点 $\text{[math]}$ 、 $\text{[math]}$ 的“等值三角形”，求 $\text{[math]}$ 的坐标；
2. （2）若以线段 $\text{[math]}$ 为底的等腰三角形是点 $\text{[math]}$ 、 $\text{[math]}$ 的“等值三角形”，求该三角形的腰长；
3. （3）若 $\text{[math]}$ 是点 $\text{[math]}$ 、 $\text{[math]}$ 的“等值三角形”，且点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
19. (2023八上·义乌月考) 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形．若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
1. （1）【理解概念】：
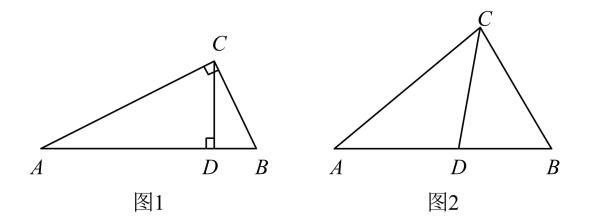
  如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB ，请写出图中两对“等角三角形”．
  ① ．；②．．
2. （2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．请你说明CD是△ABC的等角分割线．
3. （3）【应用概念】：
  在△ABC中，若∠A＝40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数．
答案解析收藏纠错 + 选题
20. (2023八下·本溪期末) 两个等腰三角形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ 在边 $\text{[math]}$ 所在的直线上 $\text{[math]}$ 连接 $\text{[math]}$ ．
1. （1）问题一：当 $\text{[math]}$ ，且点 $\text{[math]}$ 在线段 $\text{[math]}$ 上移动时，则 $\text{[math]}$ ， $\text{[math]}$ 之间有怎样的数量关系？请说明理由；
2. （2）问题二：当 $\text{[math]}$ ，且点 $\text{[math]}$ 还在线段 $\text{[math]}$ 上移动，此时 $\text{[math]}$ ， $\text{[math]}$ 之间有怎样的数量关系？请说明理由；
  随着探究的深入，得出一些基本的结论：当点 $\text{[math]}$ 在直线 $\text{[math]}$ 上移动，所处的位置不同， $\text{[math]}$ ， $\text{[math]}$ 可能的数量关系是什么？ $\text{[math]}$ 直接写出数量关系即可 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2021八上·介休期中) 在“综合与探究”课上，张老师让每名同学在练习本上画出一个长方形，随后以该长方形为基本图形，以小组为单位编制一道综合探究题．经过思考和讨论，励志小组向全班同学分享了他们编拟的试题，得到了侯老师的认可，同学们也眼前一亮，纷纷动手，开始了探究．请你也跟他们一起来完成这道试题吧．如图1，分别以长方形OABC的边OC，OA所在直线为x轴、y轴，建立平面直角坐标系，已知AO＝10，AB＝6，点E在线段OC上，以直线AE为轴，把△OAE翻折，点O的对应点D恰好落在线段BC上．
1. （1）分别求点D，E的坐标．
2. （2）如图2，若直线AD与x轴相交于点F，求直线AD表达式及点F的坐标．
3. （3）在（2）的条件下，P是x轴上的一动点，是否存在以A，P，F为顶点的三角形是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．
4. （4）在本题的探究过程中，你感悟到哪些数学思想，请至少写出两条．
答案解析收藏纠错 + 选题
22. (2024八上·深圳期末) 如图，直线l₁：y＝x＋3与过点A（3，0）的直线l₂交于点C（1，m），与x轴交于点B．
1. （1）求直线l₂的解析式；
2. （2）点M在直线l₁上，MN∥y轴，交直线l₂于点N，若MN＝AB，求点M的坐标．
3. （3）在x轴上是否存在点P，使以B、C、P为顶点的三角形是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2024八上·雨花期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D在线段 $\text{[math]}$ 上运动（点D不与点B、C重合），连接 $\text{[math]}$ ，作 $\text{[math]}$ ， $\text{[math]}$ 交线段 $\text{[math]}$ 于点E ．
1. （1）当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）线段 $\text{[math]}$ 的长度为何值时， $\text{[math]}$ ？请说明理由；
3. （3）在点D的运动过程中， $\text{[math]}$ 的形状可以是等腰三角形吗？若可以，请直接写出 $\text{[math]}$ 的度数；若不可以，请说明理由．
答案解析收藏纠错 + 选题