2024年北师大版数学八（下）微素养核心突破3 垂直平分线与...

更新时间：2024-04-14 浏览次数：29 类型：复习试卷

一、选择题

1. (2023八下·龙岗期中) 如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE＝5，则DF的长度是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
2. (2023八上·埇桥期中) 如图，在△ABC中，∠ACB＝90°，分别以点A和点B为圆心，以相同的长（大于 $\text{[math]}$ AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E．若AC＝3，AB＝5，则DE等于（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八下·东阿期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．分别以点A，C为圆心，大于 $\text{[math]}$ 长为半径作弧，两弧交于点E，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 于点O．若点O是 $\text{[math]}$ 的中点，则 $\text{[math]}$ 的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
4. (2023八下·珠海期中) 如图，在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的周长为 $\text{[math]}$ ，分别以A、B两点为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧相交于点M ， N ，连接 $\text{[math]}$ 与 $\text{[math]}$ 相交于点D ，则 $\text{[math]}$ 的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·榕城期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 、 $\text{[math]}$ 的垂直平分线的交点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·揭东期中) 如图，在 $\text{[math]}$ 中，直线 $\text{[math]}$ 是线段 $\text{[math]}$ 的垂直平分线，若 $\text{[math]}$ ， $\text{[math]}$ 的周长为13，则 $\text{[math]}$ 的周长为（）

A . 26 B . 16 C . 19 D . 22

答案解析收藏纠错 + 选题
7. (2022八下·潢川期中) 如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC、AD于点E、F，若BE=3，AF=5，则矩形ABCD的周长为（）

A . 24 B . 16 C . 12 D . 8

答案解析收藏纠错 + 选题
8. (2023八下·新田期中) 如图，在矩形ABCD中，对角线AC与BD交于点O，∠BAD的平分线交BC于E，若 $\text{[math]}$ ，则∠COE=（　　　）

A . 45 $\text{[math]}$ B . 60 $\text{[math]}$ C . 75 $\text{[math]}$ D . 30 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八下·港南期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ 的周长等于12，则 $\text{[math]}$ 的长是（）

A . 6 B . 10 C . 12 D . 24

答案解析收藏纠错 + 选题
10. (2018八下·青岛期中) 直线 $\text{[math]}$ 与表示三条相互交叉的公路，现要三条公路的内部建个货物中转站，要求它到三条公路的距离相等，那么选择油库的位置有（）处

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·宁远期中) 如图，矩形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， E为 $\text{[math]}$ 上一点， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
12. (2024七上·通川期末) 如图，点O为直线 $\text{[math]}$ 上一点，过点O作射线 $\text{[math]}$ ，使 $\text{[math]}$ ，将一块透明的三角尺直角顶点放在点O处，并绕点O旋转一周，在旋转过程中，当直线 $\text{[math]}$ 恰好平分锐角 $\text{[math]}$ 时， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023八下·安庆期中) 如图，在锐角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平分线AD交BC于点D，点M，N分别是线段AD和AB上的两个动点，则 $\text{[math]}$ 的最小值是．

答案解析收藏纠错 + 选题
14. (2023八下·宝安期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的外角平分线与边 $\text{[math]}$ 的垂直平分线交于点D，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2022八下·兰州期中) 如图，在△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝4，CF＝1，则AC的长为．

答案解析收藏纠错 + 选题
16. (2021八下·湘东期中) 已知如图等腰△ABC ， AB=AC ， ∠BAC=120°，AD⊥BC于点D ，点N是BA延长线上一点，点M是线段AD上一点，MN=MC ，下列结论中正确的结论序号是．
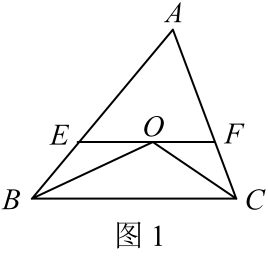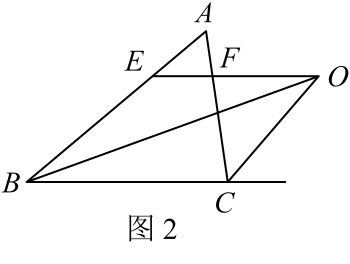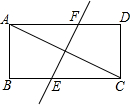
①∠ACM=∠ANM；②∠ANM+∠NCB=90°；③NC=NM；④AM+AN=AB ．

答案解析收藏纠错 + 选题

三、作图题

17. (2023八下·陈仓期中) 如图，两公路 $\text{[math]}$ 与 $\text{[math]}$ 相交于点O，两公路内侧有两工厂C和D，现要修建一货站使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题
18. (2021八下·城阳期中) 请用直尺、圆规作图，不写作法，但要保留作图痕迹．
已知：如图，四边形ABCD．
求作：点P，使点P在四边形ABCD内部，PB＝PC，并且点P到∠BAD两边的距离相等．

答案解析收藏纠错 + 选题

四、解答题

19. (2022八上·綦江期中) 已知在 $\text{[math]}$ 中，∠CAB的平分线AD与BC的垂直平分线DE交于点D， DM丄AB与M， DN丄AC交AC的延长线于N，你认为BM与CN之间有什么关系？试证明你的发现.

答案解析收藏纠错 + 选题
20. (2023八下·永安期中) 用三角尺可以画角平分线：如图所示，在已知 $\text{[math]}$ 的两边上分别取点M，N，使 $\text{[math]}$ ，再过点M画 $\text{[math]}$ 的垂线，过点N画 $\text{[math]}$ 的垂线，两垂线交于点P，那么射线 $\text{[math]}$ 就是 $\text{[math]}$ 的平分线.请你证明这一结论.

答案解析收藏纠错 + 选题

五、综合题

21. (2023八下·珠山期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一点， $\text{[math]}$ 垂直平分 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 为等腰三角形．
2. （2）若 $\text{[math]}$ ，则线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足什么数量关系？并说明理由，
答案解析收藏纠错 + 选题
22. (2022八下·本溪期中) 如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF，ON于点B，点C，连接AB，PB．
1. （1）如图1，当P，Q两点都在射线ON上时，则线段AB与PB的数量关系是；
2. （2）如图2，当P，Q两点都在射线ON的反向延长线上时线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2022八下·盐湖期中) 数学课上，老师提出了如下问题：
尺规作图：作△ABC中BC边上的高线．
已知：△ABC．
求作：△ABC中BC边上的高线AD．
下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程．
作法：如图，
①以点B为圆心，以BA长为半径作弧，以点C为圆心，以CA长为半径作弧，两弧在BC下方交于点E；
②连接AE交BC于点D．
所以线段AD是△ABC中BC边上的高线．
根据小东设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形．（保留作图痕迹）
2. （2）小乐和小马帮助小东完成下面的证明．
  小乐证明：
  ∵ $\text{[math]}$ ， $\text{[math]}$ ，
  ∴点B，C分别在线段AE的垂直平分线上（依据1）
  ∴BC垂直平分线段AE．
  ∴线段AD是△ABC中BC边上的高线．
  小马证明：
  ∵ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
  ∴△ABC≌△EBC
  ∴ $\text{[math]}$
  又∵ $\text{[math]}$
  ∴ $\text{[math]}$ （依据2）
  线段AD是△ABC中BC边上的高．
  上述证明过程中的“依据1”和“依据2”分别是什么？
3. （3）请你用不同于小东作图的方法完成老师提出的问题．（尺规作图，不写作法，只保留作图痕迹）
4. （4）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则BC边上的高AD的长度为．
答案解析收藏纠错 + 选题
24. (2023八下·东明期中)
1. （1）如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的平分线交于点O，过点O作 $\text{[math]}$ 分别交 $\text{[math]}$ 于点E，F，则线段 $\text{[math]}$ 与 $\text{[math]}$ 之间有怎样的数量关系？说明你的理由：
2. （2）如图2，若 $\text{[math]}$ 中 $\text{[math]}$ 的平分线 $\text{[math]}$ 与三角形外角平分线 $\text{[math]}$ 交于点O，过O点作 $\text{[math]}$ 交 $\text{[math]}$ 于点E，交 $\text{[math]}$ 于点F，直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系.
答案解析收藏纠错 + 选题
25. (2020八下·简阳期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的平分线与 $\text{[math]}$ 的中垂线 $\text{[math]}$ 交于点E，过点 $\text{[math]}$ 作 $\text{[math]}$ 边的垂线垂足为N，过点E作 $\text{[math]}$ 延长线的垂线，垂足为M.
1. （1）求证： $\text{[math]}$ ；
2. （2）若， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题