车型 | A | B |
汽车运载量(吨/辆) | 5 | 8 |
汽车运费(元/辆) | 600 | 800 |
销售时段 | 销售数量(单位:辆) | 销售收入(单位:万元) | |
A | B | ||
第一周 | 5 | 3 | 59 |
第二周 | 8 | 5 | 96.4 |
(进价、售价均保持不变,利润=销售收入一进货成本)
根据题意,甲、乙两名同学分别列出如下方程:
甲: , 解得
, 经检验
是原方程的解.
乙: , 解得
, 经检验
是原方程的解.
则甲所列方程中的表示,乙所列方程中的
表示;
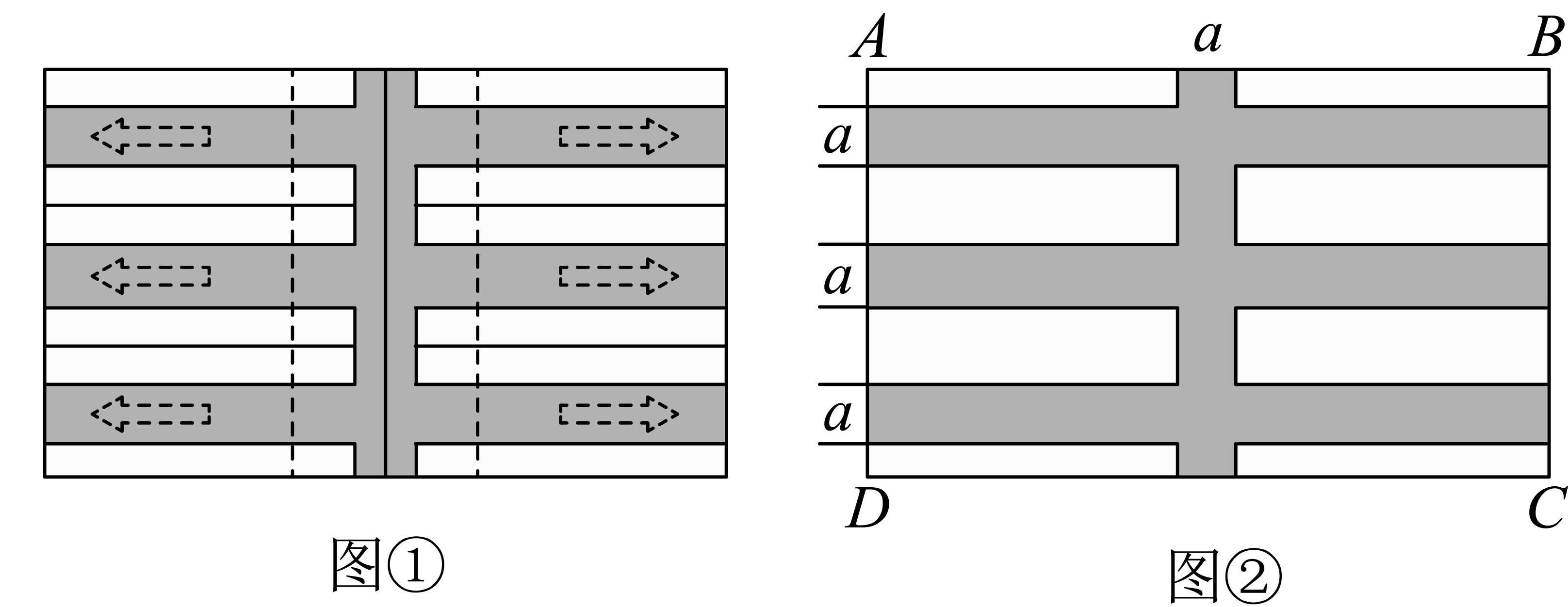
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:

【阅读理解】我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式 的取值范围。
解:
∵x取任何实数,总有 ,∴
。
因此,无论x取任何实数, 的值总是不小于-4的实数。
特别的,当x=3时, 有最小值-4
①将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. B.
C. D.
②请利用上面【阅读理解】提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
如何确定木板分配方案? | ||
素材1 | 我校开展爱心义卖活动,小艺和同学们打算推销自己的手工制品.他们以每块15元的价格买了100张长方形木板,每块木板长和宽分别为80cm,40cm. | |
素材2 | 现将部分木板按图1虚线裁剪,剪去四个边长相同的小正方形(阴影).把剩余五个矩形拼制成无盖长方体收纳盒,使其底面长与宽之比为3:1.其余木板按图2虚线裁剪出两块木板(阴影是余料),给部分盒子配上盖子.
| |
素材3 | 义卖时的售价如标签所示: | |
问题解决 | ||
任务1 | 计算盒子高度 | 求出长方体收纳盒的高度. |
任务2 | 确定分配方案1 | 若制成的有盖收纳盒个数大于无盖收纳盒,但不到无盖收纳盒个数的2倍,木板该如何分配?请给出分配方案. |
任务3 | 确定分配方案2 | 为了提高利润,小艺打算把图2裁剪下来的余料(阴影部分)利用起来,一张矩形余料可以制成一把小木剑,并以5元/个的价格销售.请确定木板分配方案,使销售后获得最大利润. |
|
题目:某商店准备购进甲、乙两种商品,甲种商品每件的进价比乙种商品每件的进价多20元,用2000元购进甲种商品和用1200元购进乙种商品的数量相同.求甲、乙两种商品每件的进价各是多少元. |
||
|
方法 |
分析问题 |
列出方程 |
|
解法一 |
设…… 等量关系:甲商品数量=乙商品数量 |
|
|
解法二 |
设…… 等量关系:甲商品进价-乙商品进价=20 |
|
任务:
A.甲种商品每件进价x元
B.乙种商品每件进价x元
C.甲种商品购进x件
如何设计种植方案?
素材1:
某校为响应国家政策,在校内平方米的土地上进行种植课实践,现有
、
,
三种作物的相关信息如表所示
已知
株
作物和
株
作物的产量共为
千克:
株
作物和
株
作物的产量共为
千克.
|
|
|
|
每平方米种植株树 | |||
单株产量 | | | |
素材2:
由于作物植株间距较大,可增加
作物每平方米的种植株树
经过实验发现,每平方米种植
作物每增加
株,
作物的单株产量减少
千克
而
,
单株产量不发生变化.
素材3:
若同时种植 ,
,
三种作物,实行分区域种植.
问题解决:
求 ,
的值.
要使作物每平方米产量为
千克,则每平方米应种植多少株?
设这平方米的土地中有
平方米用于种植
作物,且每平方米的产量最大:有
平方米用于种植
作物,剩余的全用来种植
作物,
,
均为正整数
当这
平方米总产量为
千克时,求这三种作物的种植方案.