



①求y与x的函数解析式;
②y是否有最大值,若有,求出y的最大值;若没有,请说明理由.
①;
②设 , 则
(用含
的式子表示);
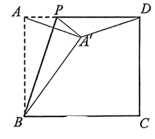
如图1中的是黄金三角形.
如图2,在菱形中,
,
, 求菱形较长对角线的长.
【操作】如图1,在矩形中,点M在边
上,将矩形纸片
沿
所在的直线折叠,使点D落在点
处,
与
交于点N .
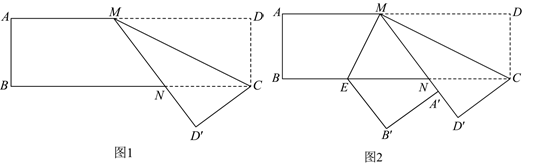
【猜想】
∵矩形纸片沿
所在的直线折叠
∴
∵四边形是矩形
∴(矩形的对边平行)
∴()
∴(等量代换)
∴()
如图2,继续将矩形纸片折叠,使
恰好落在直线
上,点A落在点
处,点B落在点
处,折痕为
.
⑴猜想与
的数量关系,并说明理由;
⑵若 ,
, 求
的长.



