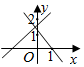
 B .
B . 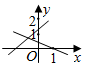 C .
C . 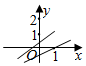 D .
D . 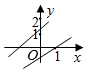

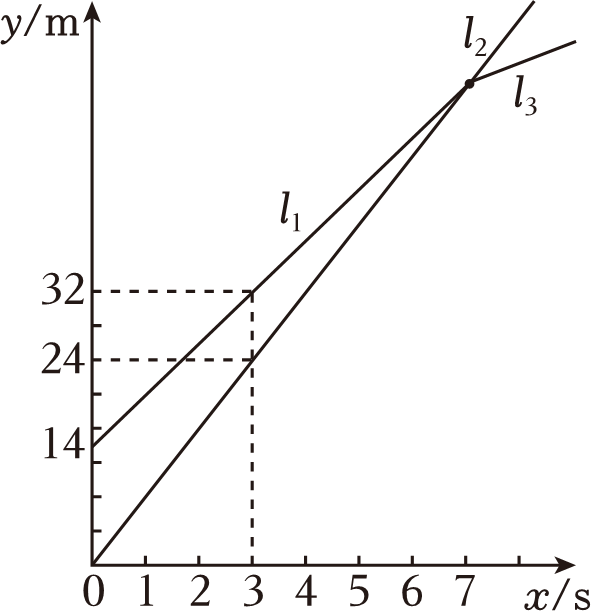
①A , B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后1.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或
.
其中正确的结论有( )

①关于的方程
的解为
;
②一次函数(
)图像上任意不同两点
和
满足:
;
③若(
),则
;
④若 , 且
, 则当
时,
.

①的周长为
;
②;
③;
④点P为射线上一动点,
的最小值为
.

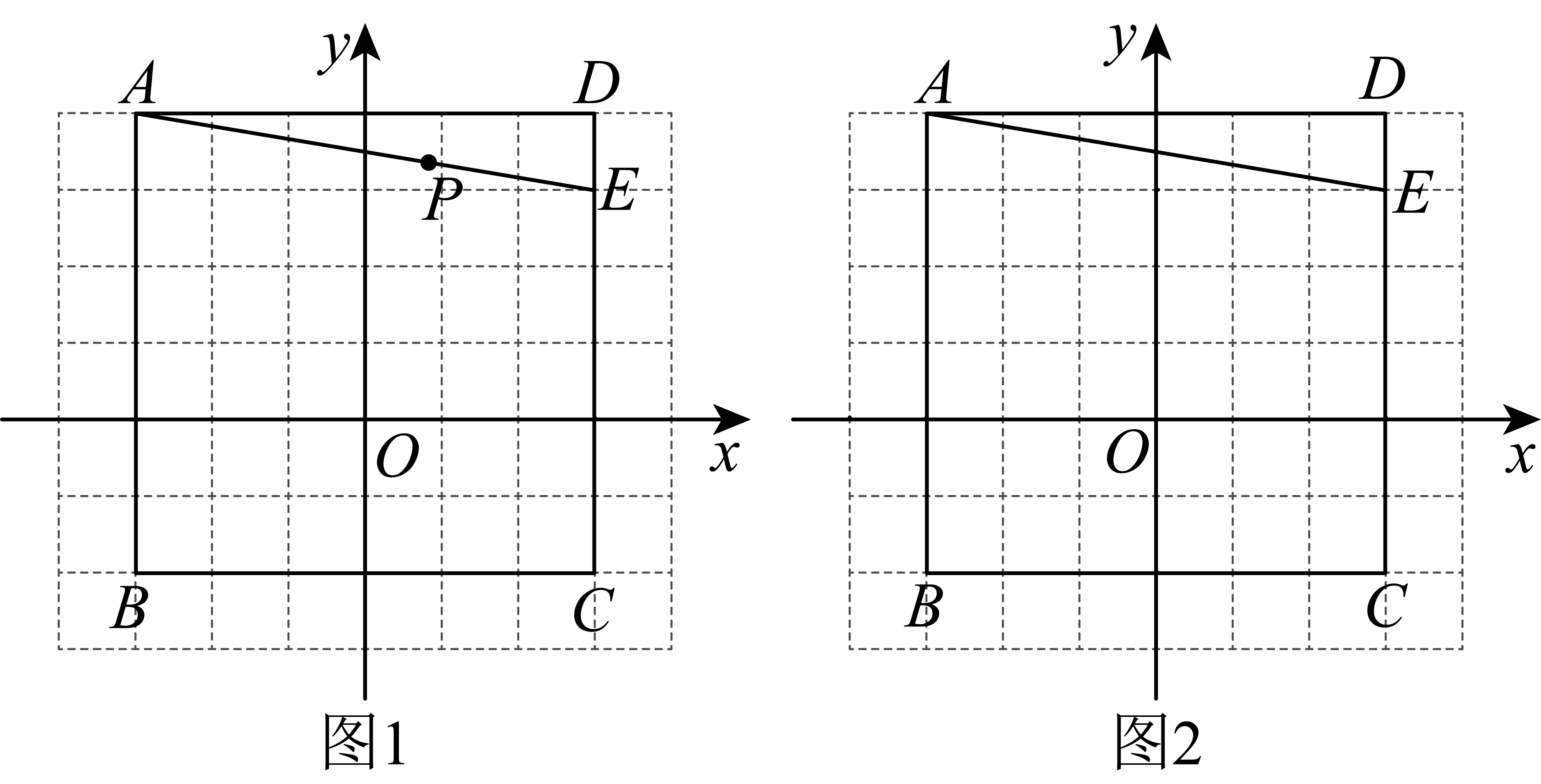
①试说明在点的运动过程中,
的面积是否为定值,若是请求出定值,若不是请说明理由;
②点从
运动到
的过程中,点
的运动路径长为 ▲ .