




经过组内合作交流,小明得到了如下的解决方法:延长到点E , 使
.请根据小明的方法思考:

如图2,已知 ,
,
, P为
的中点.若A , C , D共线,求证:
平分
;

①当D在点B的右侧,且∠ADC=30°,∠AEC=50°,∠BAD= ▲ °,∠PAC= ▲ °;
②过点E作EF⊥AC , 垂足为F , 记∠AEF=x度,∠ADB=y度,直接写出y与x的关系式.

①如图3, , 则
▲ (用含
的代数式表示).
②若光线 , 判断
与
的位置关系,并说明理由.
在行驶过程中,后车驾驶员平视前方,且视点会高于反射点
(如图4),因此小亮认为反射光线
应与水平视线
成一定角度.学习小组设计了如图5所示的模拟实验装置,使入射光线
, 当
与
所成夹角为
时,求
的度数.


 B .
B .  C .
C .  D .
D . 
 B .
B . 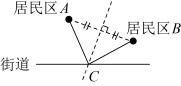 C .
C . 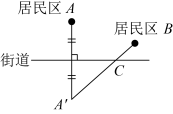 D .
D . 


【问题提出】在前面的学习中我们通过折纸可以找出一个角的平分线,还可以折出过一个点且与已知直线垂直的直线.那我们能否通过折纸的方式找到过直线外一点且与已知直线平行的直线呢?

①如图1,在纸上画出一条直线 , 在
外取一点
. 过点
折叠纸片,使得点
的对应点
落在直线
上(如图2),记折痕
与
的交点为
, 将纸片展开铺平.则
▲
;
②再过点将纸片进行折叠,使得点
的对应点
落在直线
上(如图3),再将纸片展开铺平(如图4).此时王玲说,
就是
的平行线.王玲的说法正确吗?请写出过程予以证明;

试验种子数n(粒) | 50 | 200 | 500 | 1000 | 3000 |
发芽频数m | 45 | 188 | 476 | 951 | 2850 |
发芽频率 | 0.9 | 0.94 | 0.952 | 0.951 | 0.95 |


|
试验次数 |
20 |
40 |
60 |
80 |
100 |
1000 |
|
“指针落在灰色区域内”的次数 |
6 |
11 |
15 |
21 |
25 |
250 |
|
“指针落在灰色区域内”的频率 |
0.3 |
0.275 |
0.25 |
0.2625 |
0.25 |
0.25 |
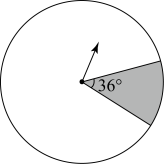
根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率是.(精确到百分位)
|
试验的粒数n |
20 |
80 |
100 |
200 |
400 |
800 |
1000 |
1500 |
|
发芽的粒数m |
14 |
54 |
67 |
132 |
264 |
532 |
670 |
1000 |
|
发芽的频率 |
0.7 |
0.675 |
0.67 |
0.66 |
0.66 |
0.665 |
a |
0.667 |
|
转动转盘的次数 |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“铅笔”区域的次数 |
68 |
111 |
136 |
345 |
564 |
701 |
|
落在“铅笔”区域的频率 |
_______ |
_______ |
_______ |
_______ |
_______ |
_______ |

| 实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| “兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
| 相应频率 | | | | | | | |
