


如图 , 若
,
, 则
如图 ,
、
和
的数量关系为 .
【问题提出】在前面的学习中我们通过折纸可以找出一个角的平分线,还可以折出过一个点且与已知直线垂直的直线.那我们能否通过折纸的方式找到过直线外一点且与已知直线平行的直线呢?

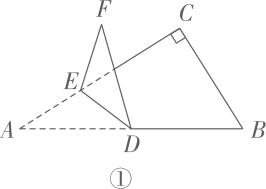
①如图1,在纸上画出一条直线 , 在
外取一点
. 过点
折叠纸片,使得点
的对应点
落在直线
上(如图2),记折痕
与
的交点为
, 将纸片展开铺平.则
▲
;
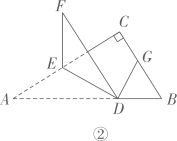
②再过点将纸片进行折叠,使得点
的对应点
落在直线
上(如图3),再将纸片展开铺平(如图4).此时王玲说,
就是
的平行线.王玲的说法正确吗?请写出过程予以证明;
问题背景:
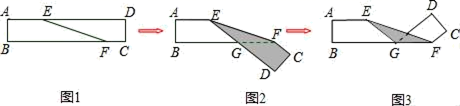
数学课上,同学们以“长方形纸带的折叠”为主题开展数学活动,已知长方形纸带的边 ,
,
,点
为线段AD上一动点
,将纸片折叠,使点B和点
重合,产生折痕EF,点E是折痕与边AD的交点,点F是折痕与边BC的交点.

动手操作:
实践探究:
①小静发现图中无论点 如何移动,
始终成立,请说明理由;
②小东发现折叠后所形成的角,只要知道其中一个角的度数,就能求出其它任意一角的度数,若 ,求
的大小.


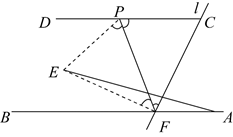
①如图1,在纸上画出一条直线BC,在BC外取一点P.过点P折叠纸片,使得点C的对应点落在直线BC上(如图2),记折痕DE与BC的交点为A,将纸片展开铺平.则
▲
.
②再过点P将纸片进行折叠,使得点E的对应点落在直线DP上(如图3),再将纸片展开铺平(如图4).此时王玲说,PF就是BC的平行线.王玲的说法正确吗?请写出过程予以证明;
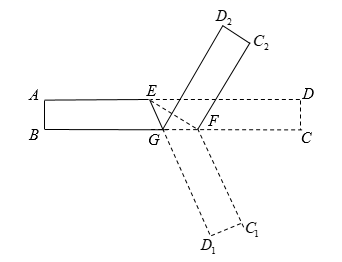
如图2, ,
, 则
▲

结论:两个角的两边分别平行,则这两个角 ▲ 或 ▲
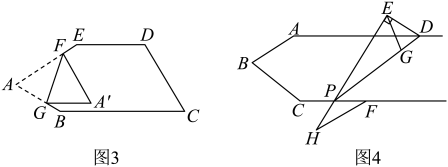
②在图3中,五边形 , 点G、F分别在
、
上,将∠A沿
翻折得到
,
,
,
,
, 求
的度数.