如图,数轴上两点 ,
所表示的数分别为
, 4,点
,
是数轴上两动点,点
从点
出发以每秒1个单位的速度向
运动,同时点
从
点出发以每秒2个单位的速度向
运动,当
时,求此时
点对应的数.
若点为线段
的中点,点
为线段
的中点,点
在线段
上运动时,线段
的长度是否发生变化?请说明理由;
当点运动的同时,点
从点
出发,以每秒3个单位长度的速度沿着数轴向左匀速运动。
①在运动过程中,点表示的数为_▲_,点
表示的数为_▲_.
②求运动多少秒时,点与点
相距3个单位长度?
如图2,若线段与
分别为同一钟表上某一时刻的时针与分针,
, 在时针与分针转动过程中,经过分钟后,
的度数第一次等于
。
主题:制作一个无盖长方形盒子.
步骤1:按照如图所示的方式,将正方形纸片的四个角剪掉四个大小相同的小正方形.
步骤2:沿虚线折起来,就可以做成一个无盖的长方体盒子.
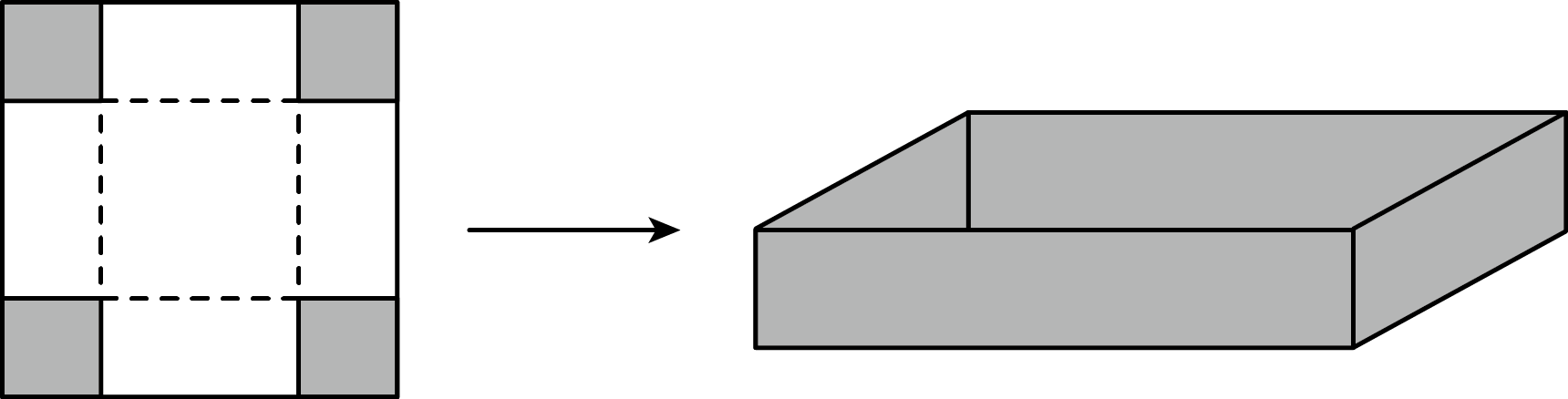
如果原正方形纸片的边长为a,剪去的正方形的边长为b,则折成的无盖长方体盒子的高、底面积、容积分别为、、(请你用含a,b的代数式来表示).
如果 , 剪去的小正方形的边长按整数值依次变化,即分别取
,
,
,
,
,
,
,
,
,
时,折成的无盖长方体的容积分别是下表数据,请求出m和n分别是多少?
剪去正方形的边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
容积/ | 324 | 512 | m | n | 500 | 384 | 252 | 128 | 36 | 0 |
观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时,所得的无盖长方体的容积最大,此时最大容积是多少?
c/cm | |||||
V/cm3 |
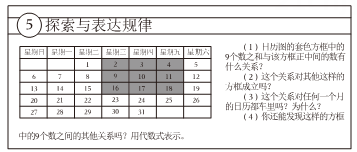

请解答教材中的(1)、(2)问。
活学活用
小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数 , 排成如图形式,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
如图是某月的日历.
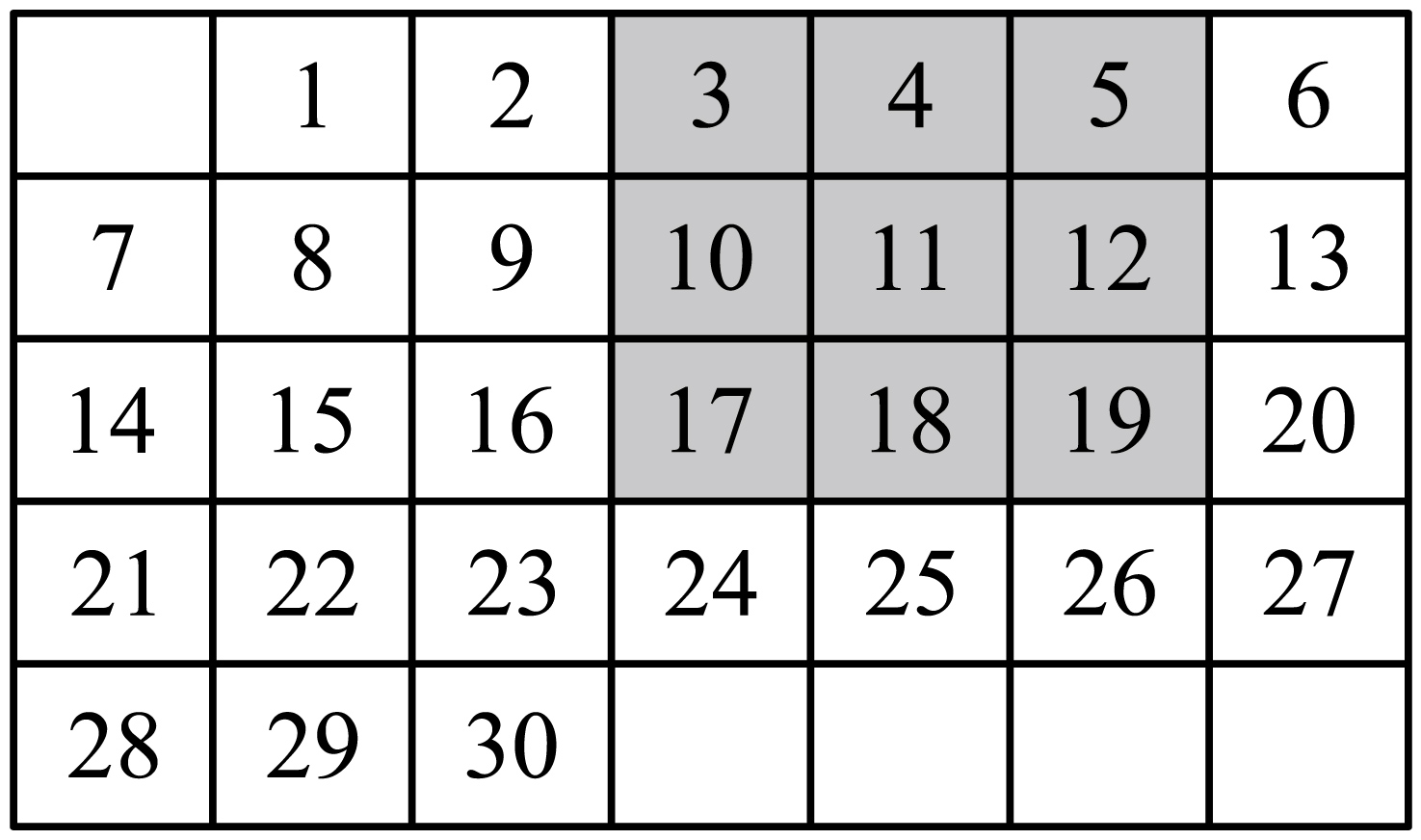
①带阴影的方框中的9个数之和与方框正中的数有什么关系?
②不改变方框的大小如果将带阴影的方程移至其他几个位置试一试,上述关系还成立吗?如成立,请说明为什么成立.
小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图形式,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
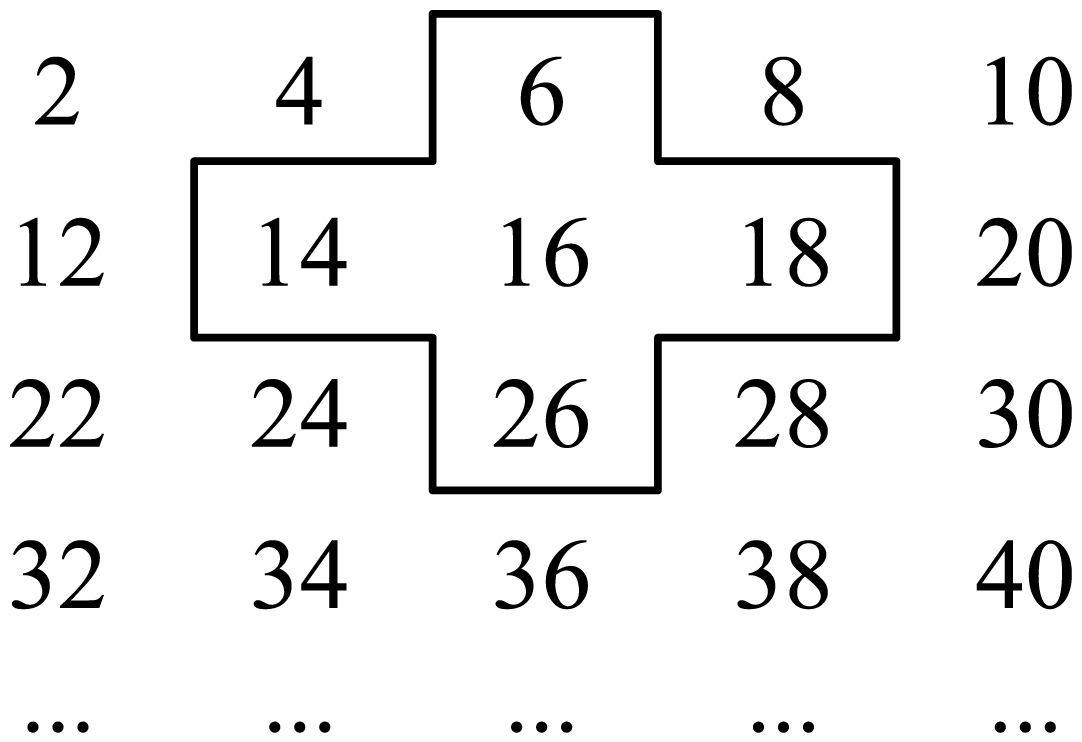
①十字框中的五个数的和与中间的数16有什么关系?
②设中间的数为x,用代数式表示十字框中的五个数的和;
③若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
商品条形码在生活中随处可见,它是商品的身份证.条形码是由13位数字(每个数字都是由大于等于0且小于等于9的整数)组成,前12位数字分别表示“国家代码、出口商识别码和商品代码”相关信息,如图①693是代表中国,49170代表出口商识别码,0940代表商品代码,第13位数字2为“校验码”.其中,校验码是用来校验商品条形码中前12位数字代码的正确性,它的编制是按照特定算法得来的,具体算法如下(以图①为例):
步骤 | 举例说明 | |||||||||||||
步骤1:自左向右编号: | 某商品的条形码:693489170940X(X为校验码) | |||||||||||||
位置序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
代码 | 6 | 9 | 3 | 4 | 9 | 1 | 7 | 0 | 0 | 9 | 4 | 0 | X | |
步骤2:求前12位数字中偶数位上的数字之和s; |
| |||||||||||||
步骤3:求前12为数字钟奇数位上的数字之和t; |
| |||||||||||||
步骤4:计算 |
| |||||||||||||
步骤5:取大于或等于m且为10的最小整数倍数n; |
| |||||||||||||
步骤6:计算n与m的差就是校验码X. |
| |||||||||||||
【知识运用】请回答下列问题:
步骤1:自左向右编号,共13位;
步骤2:求前12位数字中偶数位上的数字之和;
步骤3:求前12位数字中奇数位上的数字之和;
步骤4:计算与t的和
;
步骤5:取大于或等于m且为10的最小整数倍数;
步骤6:计算n与m的差就是校验码.

若关于
的一元一次方程
和
互为“阳光方程”,则关于
的一元一次方程
的解为 .
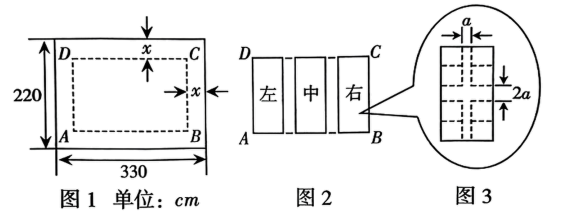
如图1是长方形宣传牌,长 , 宽
, 中间可以用来设计的部分是长方形
, 且
. 四周空白部分的宽度相等,设四周宽度为
;
如图2,为了美观,将长方形分割成大小相等的左、中、右三个小长方形栏目,栏目与栏目之间的中缝间距相等;
如图3,每个栏目划出8个小正方形方格,中间有十字间隔,竖行两列中间间隔和横向中间间隔宽度比为 .


若
旋转到图
的位置,
的度数为多少?
用含
的代数式表示
在旋转过程中,若
, 求此时
的值.
将两块三角板如图1所示放置,∠ACB=90°,∠BAC=45°,∠CDE=90°,∠DCE=30°,AC=CD=6.将△DCE 绕着点C顺时针旋转时CF平分∠BCD.

如图,在直角△ABC中,∠ACB=90°,点A在直线MN上,点D、E在直线MN上运动(点D不与点A重合),且始终满足CE平分∠BCD.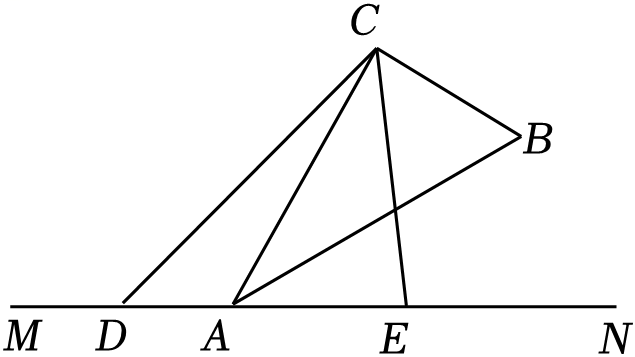

如图2,若三角板AOB不动,将三角板COD绕点O以每秒6°的速度按顺时针方向旋转一周,经过t秒时,三角板COD的边OC恰好分.
①此时t=秒:
②此时=°=;
如图2,在(1)的条件下,边OC恰好平分.时,同一时刻三角板AOB开始也绕点O以每秒
的速度按相同方向旋转,那么再经过多长时间边OA与边OD第一次重合?(如图3)请说明理由;
如图3,在(2)的条件下,当边OA与边OD第一次重合时,两个三角板同时按顺时针方向再次转动一周后停止,请问两个三角板再次转动后,经过多少秒,边OB恰好平分请说明理由.
【问题背景】:已知O是直线上的一点,射线
在直线
的上方,
, 将直角三角板
的直角顶点放在O处,且直角三角板在直线
的上方.
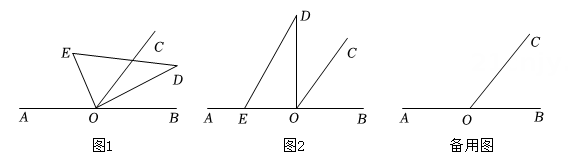
如图1,若 , 则
;
将图2中的三角板绕点O以每秒
的速度顺时针旋转
, 设运动时间为t秒,是否存在t值,使
?若不存在,请说明理由;若存在,请求出t的值.
定义回顾:从一个角的顶点出发,将这个角分成两个相等的角的射线,叫做这个角的平分线.角的平分线也可以通过折纸完成,如图(1),将含有的纸片经过顶点P对折叠,折痕
所在的射线就是
的平分线.利用角的平分线的定义,可以进行角的度数的计算.

问题解决:
①若 ,
, 求
的度数;
②若 , 求
的度数(用含
的式子表示);
【问题背景】:已知O是直线上的一点,射线
在直线
的上方,
, 将直角三角板
的直角顶点放在O处,且直角三角板在直线
的上方.

【问题解决】:
(1)如图1,若 , 则
______
;
(2)若恰好平分
, 求
和
的度数;
【拓展延伸】:
(3)将图2中的三角板绕点O以每秒
的速度顺时针旋转
, 设运动时间为t秒,是否存在t值,使
?若不存在,请说明理由;若存在,请求出t的值.