
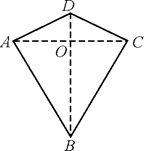
①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC·BD.其中正确的结论有( )
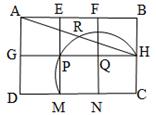



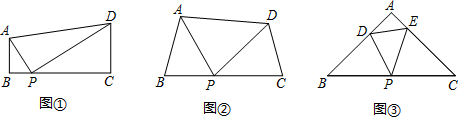
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为.
① 表示的点与数表示的点重合;
②若数轴上A、B两点之间距离为8(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是;
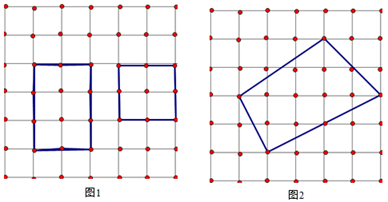
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.

计算:拼成的大正方形的面积为5,边长为 ,可表示成
;
剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
拼图:以图(3)中的虚线为边,拼成一个边长为 的大正方形,如图(4).

问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
①计算:拼成的大正方形的面积为,边长为,可表示成;
②剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
③拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.
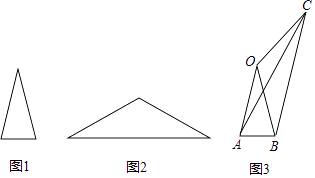
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是什么;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
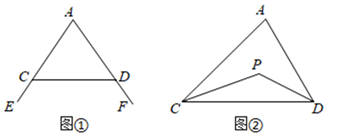
已知:如图①,∠FDC与∠ECD分别为 ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系,并证明你探究的数量关系.
已知:如图②,在 ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠A与∠P的数量关系,并证明你探究的数量关系.
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠A+∠B与∠P的数量关系.


【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB,∠EDF=90,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系。
【探究发现】

小华同学根据学习函数的经验,分别对函数 ,随自变量x的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| | 4.47 | 5.24 | 5.86 | 5.96 | 4.72 | 4.00 | |
| | 6.00 | 5.86 | 5.23 | 3.98 | 2.46 | 1.06 | 0 |
请你补全表格的相关数值,保留两位小数.

如图1,正五边形ABCDE中,




(问题探究)小明同学的思路是:如图2,在BE上截取BF=AD,连接CA,CB,CD,CF.……请你按照小明的思路完成上述问题的证明过程.
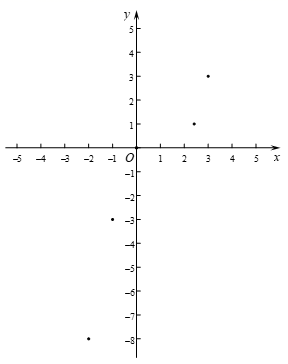
|
x |
… |
-2 |
-1 |
0 |
1 |
2 |
| 3 | … |
| y | … | -8 | -3 | 0 | m | n | 1 | 3 | … |
请直接写出:m=,n=;
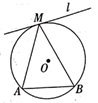
如图, 是
的弦,点
是
上的一点,在直线
上方找一点
,使得
,画出
,并说明理由;
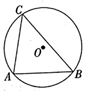
如图, 是
的弦,直线
与
相切于点
,点
,是直线
上异于点
的任意一点,请在图中画出图形,试判断
的大小关系;并说明理由;
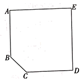
如图,有一个平面图为五边形ABCDE的展览馆,其中 ,
,
.展览馆保卫人员想在线段
上选一点
安装监控装置,用来监视边
,现只要使
最大,就可以让监控装置的效果达到最佳,问在线段
上是否存在点
,使
最大?若存在,请求出符合条件的
的长,若不存在,请说明理由.
如图1,AB为⊙O的直径,请在⊙O上求作一点P,使∠ABP=45°.(不必写作法)

如图2,等腰直角三角形△ABC中,∠A=90°,AB=AC=3 ,D是AB上一点,AD=2
,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
如图3,为矩形足球场的示意图,其中宽AB=66米、球门EF=8米,且EB=FA.点P、Q分别为BC、AD上的点,BP=7米,∠BPQ=135,一位左前锋球员从点P处带球,沿PQ方向跑动,球员在PQ上的何处才能使射门角度(∠EMF)最大?求出此时PM的长度.