浙教版备考2021年中考数学三轮冲刺复习专题15 对称与位移

更新时间：2021-05-16 浏览次数：157 类型：三轮冲刺

一、单选题

1. (2020·宁波模拟) 下列图形中，是中心对称图形但不是轴对称图形的有（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019·海宁模拟) 如图，矩形ABCD中，E是AB的中点，F是AD边上的一个动点，已知AB＝4，AD＝2 $\text{[math]}$ ，△GEF与△AEF关于直线EF成轴对称.当点F沿AD边从点A运动到点D时，点G的运动路径长为（）

A . 2 $\text{[math]}$ B . 4π C . 2π D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·绍兴模拟) 已知点P（﹣1﹣2a，5）关于x轴的对称点和点Q（3，b）关于y轴的对称点相同，则A（a，b）关于x轴对称的点的坐标为（）

A . （1，﹣5） B . （1，5） C . （﹣1，5） D . （﹣1，﹣5）

答案解析收藏纠错 + 选题
4. (2019·温州模拟) 如图，是一个三角板，则下列选项中可能是由该图经过一次轴对称变换后得到的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2020·湖州模拟) 三角形纸片ABC中，∠C＝90°，甲折叠纸片使点A与点B重合，压平得到的折痕长记为m；乙折叠纸片使得CA与CB所在的直线重合，压平得到的折痕长记为n，则m，n的大小关系是（）

A . m≤n B . m＜n C . m≥n D . m＞n

答案解析收藏纠错 + 选题
6. 如图，矩形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 分别在坐标轴上，且点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 轴正方向平移 $\text{[math]}$ 个单位，得到矩形 $\text{[math]}$ ， $\text{[math]}$ 再以点 $\text{[math]}$ 为旋转中心，把矩形 $\text{[math]}$ 顺时针方向旋转 $\text{[math]}$ ，得到矩形 $\text{[math]}$ ″ $\text{[math]}$ ″ $\text{[math]}$ ″ $\text{[math]}$ ″ $\text{[math]}$ ″， $\text{[math]}$ ″， $\text{[math]}$ ″， $\text{[math]}$ ″ $\text{[math]}$ ，则点 $\text{[math]}$ 所经过的路线为 $\text{[math]}$ ″的长为（）

A . 11 B . 12 C . 4+5 $\text{[math]}$ D . 4+ $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019·吴兴模拟) 等腰直角三角形ABC和等腰直角三角形ADE中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ 固定， $\text{[math]}$ 绕点A顺时针旋转一周，在 $\text{[math]}$ 旋转过程中，若直线CE与直线BD交点为P，则 $\text{[math]}$ 面积的最小值为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 4.5

答案解析收藏纠错 + 选题
8. (2023九上·南昌月考) 如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG，点B的对应点E落在边CD上，且DE=EF，若AD= $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . π

答案解析收藏纠错 + 选题
9. (2021九上·阳东期末) 已知点A（x﹣2，3）与点B（x+4，y﹣5）关于原点对称，则（）

A . x＝﹣1，y＝2 B . x＝﹣1，y＝8 C . x＝﹣1，y＝﹣2 D . x＝1，y＝8

答案解析收藏纠错 + 选题
10. (2020·舟山模拟) 第一次：将点A绕原点O逆时针旋转90°得到A₁；
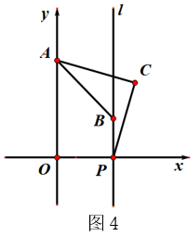
第二次：作点A₁关于x轴的对称点A₂；

第三次：将点A₂绕点O逆时针旋转90°得到A₃；

第四次：作点A₃关于x轴的对称点A₄…，

按照这样的规律，点A₃₅的坐标是（）

A . （﹣3，2） B . （﹣2，3） C . （﹣2.﹣3） D . （3.﹣2）

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·台州月考) 如图，把大正方形平均分成9个小正方形，其中有2个小正方形已被涂黑，在剩余的7个白色小正方形中任选一个也涂黑，则使整个涂黑部分成为轴对称图形的概率是．

答案解析收藏纠错 + 选题
12. (2020·临海模拟) 如图，在矩形ABCD中，AB＝12，BC＝16，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，则DF的长为

答案解析收藏纠错 + 选题
13. (2018·上城模拟) 已知图中Rt△ABC，∠B=90°，AB=BC，斜边AC上的一点D，满足AD=AB，将线段AC绕点A逆时针旋转α （0°<α <360°），得到线段ac’，连接dc’，当dc’ bc时，旋转角度α 的值为，

答案解析收藏纠错 + 选题
14. (2020·海曙模拟) 如图，在△ABC中，∠ACB为钝角，把边AC绕点A沿逆时针方向旋转90°得AD，把边BC绕点B沿顺时针方向旋转90°得BE，作DM⊥AB于点M，EN⊥AB于点N，若AB＝5，EN＝2，则DM＝.

答案解析收藏纠错 + 选题
15. (2019·三门模拟) 如图，矩形ABCD周长为30，经过矩形对称中心O的直线分别交AD，BC于点E，F.将矩形沿直线EF翻折，A′B′分别交AD，CD于点M，N，B′F交CD于点G.若MN：EM=l：2，则△DMN的周长为.

答案解析收藏纠错 + 选题
16. (2020·椒江模拟) 在平面直角坐标系中，点P（2，m）绕坐标原点O逆时针旋转 $\text{[math]}$ 后，恰好落在图中阴影区域（包括边界）内，则m的取值范围是．

答案解析收藏纠错 + 选题

三、综合题

17. (2020·宁波模拟) 如图，在下列5×5的网格中，横、纵坐标均为整点的数叫做格点，例如(0，1)、B(2，1)、C(3，3)都是格点，现仅用无刻度的直尺在网格中做如下操作：

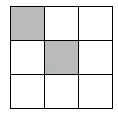
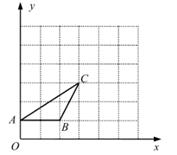
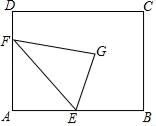
( 1 )直接写出点A关于点B旋转180°后对应点M的坐标 ▲ ；

( 2 )画出线段BE，使BE⊥AC，其中E是格点，并写出点E的坐标 ▲ ；

( 3 )找格点F，使∠EAF=∠CAB，画出∠EAF，并写出点F的坐标 ▲ 。

答案解析收藏纠错 + 选题
18. 如图，在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ .
1. （1）画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称图形 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的对称点 $\text{[math]}$ 的坐标；
2. （2）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是；
3. （3）若直线 $\text{[math]}$ 轴，与线段 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点 $\text{[math]}$ 、 $\text{[math]}$ （点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合），若将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折，点 $\text{[math]}$ 的对称点为点 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 的内部（包含边界）时，点 $\text{[math]}$ 的横坐标 $\text{[math]}$ 的取值范围是.
答案解析收藏纠错 + 选题
19. (2022八下·正定期中) 如图，在直角坐标系中，长方形 $\text{[math]}$ 的三个顶点的坐标为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 轴，点 $\text{[math]}$ 是长方形内一点（不含边界）.
1. （1）求a，b的取值范围.
2. （2）若将点P向左移动8个单位，再向上移动2个单位到点Q，若点Q恰好与点C关于 $\text{[math]}$ 轴对称，求a，b的值.
答案解析收藏纠错 + 选题
20. (2020·江干模拟) 已知一张正方形ABCD纸片，边长AB＝2，按步骤进行折叠，如图1，先将正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF.
1. （1）如图2，将CF边折到BF上，得到折痕FM，点C的对应点为C'，求CM的长.
2. （2）如图3，将AB边折到BF上，得到折痕BN，点A的对应点为A'，求AN的长.
答案解析收藏纠错 + 选题
21. (2019·新昌模拟) 在平面直角坐标系中，已知点A(0，4)，B(4，4)，点M，N是射线OC上两动点(OM＜ON)，且运动过程中始终保持∠MAN＝45°，小明用几何画板探究其中的线段关系.
1. （1）探究发现：当点M，N均在线段OB上时(如图1)，有OM²+BN²＝MN².
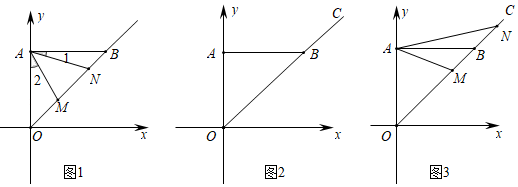
  他的证明思路如下：
  
  第一步：将△ANB绕点A顺时针旋转90°得△APO，连结PM，则有BN＝OP.
  
  第二步：证明△APM≌△ANM，得MP＝MM.
  
  第一步：证明∠POM＝90°，得OM²+OP²＝MP².
  
  最后得到OM²+BN²＝MN².
  
  请你完成第二步三角形全等的证明.
2. （2）继续探究：除(1)外的其他情况，OM²+BN²＝MN²的结论是否仍然成立？若成立，请证明；若不成立，请说明理由.
3. （3）新题编制：若点B是MN的中点，请你编制一个计算题(不标注新的字母)，并直接给出答案(根据编出的问题层次，给不同的得分).
答案解析收藏纠错 + 选题
22. (2020·丽水模拟) 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= $\text{[math]}$ (k>0，x>0)的图象上，点D的坐标为( $\text{[math]}$ ，2)。
1. （1）求k的值；
2. （2）若将菱形ABCD沿x轴正方向平移，当菱形的另一个顶点恰好落在函数y= $\text{[math]}$ (k>0，x>0)的图象上时，求菱形ABCD平移的距离。
答案解析收藏纠错 + 选题
23. (2021九上·鹿城月考) 如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD=30，DM=10.
1. （1）在旋转过程中，
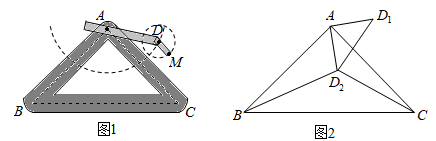
  ①当A，D，M三点在同一直线上时，求AM的长。
  
  ②当A，D，M三点为同一直角三角形的顶点时，求AM的长。
2. （2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D₁转到其内的点D₂处，连结D₁D₂ ，如图2.此时∠AD₂C=135°，CD₂=60，求BD₂的长.
答案解析收藏纠错 + 选题
24. (2020·吴兴模拟) 如图
1. （1）【问题探究】
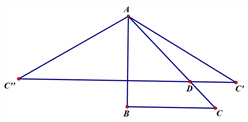
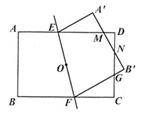
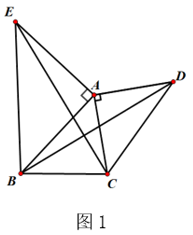
  如图1，锐角△ABC中，分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD＝90°，连接BD，CE，试猜想BD与CE的大小关系，不需要证明．
2. （2）【深入探究】
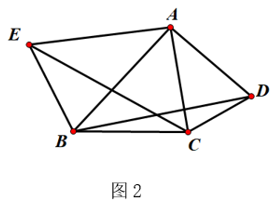
  如图2，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD，连接BD、CE，试猜想BD与CE的大小关系，并说明理由．
3. （3）【拓展应用】
  如图3，在△ABC中，∠ACB=45°，以AB为直角边，A为直角顶点向外作等腰直角△ABD，连接CD，若AC= $\text{[math]}$ ，BC=3，则CD长为.
4. （4）如图4，已知在平面直角坐标系xOy中，O为坐标原点，A（0， $\text{[math]}$ ）、P（3，0），过点P作直线l⊥x轴，点B是直线l上的一个动点，线段AB绕点A按逆时针方向旋转30°得到线段AC．则AC+PC的最小值为．
答案解析收藏纠错 + 选题