备考2022年中考数学一轮复习（湘教版）专题58 相似图形和...

更新时间：2021-09-22 浏览次数：124 类型：一轮复习

一、单选题

1. (2021九上·交城期末) 如图，△ABC内接于⊙O ， AB为⊙O的直径，D为⊙O上一点（位于AB下方），CD交AB于点E ，若∠BDC＝45°，BC＝6 $\text{[math]}$ ，CE＝2DE ，则CE的长为（）

A . 2 $\text{[math]}$ B . 4 $\text{[math]}$ C . 3 $\text{[math]}$ D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·杭州模拟) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．连接CD ，连接BE并延长交AC ， AD于点F ， G ．若BE恰好平分 $\text{[math]}$ ，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·文山模拟) 如图，在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 4 B . 8 C . 9 D . 12

答案解析收藏纠错 + 选题
4. (2021·建华模拟) 如图，大三角形与小三角形是位似图形．若小三角形一个顶点的坐标为（m ， n），则大三角形中与之对应的顶点坐标为（）

A . （﹣2m ， ﹣2n） B . （2m ， 2n） C . （﹣2n ， ﹣2m） D . （2n ， 2m）

答案解析收藏纠错 + 选题
5. (2021·道外模拟) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ 为对角线 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则下列所给的结论中，不一定正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·安徽模拟) 如图，G是△ABC的中位线MN的中点，CG的延长线交AB于点F ，则AF：FB等于（）

A . 1：2 B . 1：3 C . 2：3 D . 3：4

答案解析收藏纠错 + 选题
7. (2021·济宁) 如图，已知 $\text{[math]}$ ．

⑴以点A为圆心，以适当长为半径画弧，交 $\text{[math]}$ 于点M ，交 $\text{[math]}$ 于点N ．

⑵分别以M ， N为圆心，以大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 的内部相交于点P ．

⑶作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点D ．

⑷分别以A ， D为圆心，以大于 $\text{[math]}$ 的长为半径画弧，两弧相交于G ， H两点．

⑸作直线 $\text{[math]}$ ，交 $\text{[math]}$ ， $\text{[math]}$ 分别于点E ， F ．

依据以上作图，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
8. (2021九下·曹县期中) 如图，把 $\text{[math]}$ 沿着 $\text{[math]}$ 的方向平移到 $\text{[math]}$ 的位置，它们重叠部分的面积是 $\text{[math]}$ 面积的一半，若 $\text{[math]}$ ，则 $\text{[math]}$ 移动的距离是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·石家庄月考) △ABC的边长AB＝2，面积为1，直线PQ $\text{[math]}$ BC，分别交AB、AC于P、Q，设AP＝t，△APQ面积为S，则S关于t的函数图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2021九下·金牛月考) 如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC～△AED的是（）

A . ∠AED＝∠B B . ∠ADE＝∠C C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2020九上·鄞州期末) 如图，矩形ABCD∽矩形FAHG，连结BD，延长GH分别交BD、BC于点Ⅰ、J，延长CD、FG交于点E，一定能求出△BIJ面积的条件是（）

A . 矩形ABJH和矩形HJCD的面积之差 B . 矩形ABJH和矩形HDEG的面积之差 C . 矩形ABCD和矩形AHGF的面积之差 D . 矩形FBJG和矩形GJCE的面积之差

答案解析收藏纠错 + 选题
12. (2020九上·鄞州期末) 如果两个相似多边形的面积之比为1：4，那么它们的周长之比是( ）

A . 1：2 B . 1：4 C . 1：8 D . 1：16

答案解析收藏纠错 + 选题
13. (2020九上·靖远期末) 下列结论中，错误的有：（）
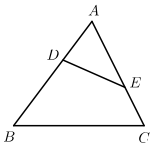
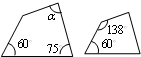
①所有的菱形都相似；②放大镜下的图形与原图形不一定相似；

③等边三角形都相似；④有一个角为110度的两个等腰三角形相似；⑤所有的矩形不一定相似.

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
14. (2019九上·南山期末) 下列说法错误的是（）

A . 所有矩形都是相似的 B . 若线段a＝5cm，b＝2cm，则a：b＝5：2 C . 若线段AB＝ $\text{[math]}$ cm，C是线段AB的黄金分割点，且AC＞BC，则AC＝ $\text{[math]}$ cm D . 四条长度依次为lcm，2cm，2cm，4cm的线段是成比例线段

答案解析收藏纠错 + 选题
15. (2019九上·大田期中) 如图所示的两个四边形相似，则α的度数是(　　)

A . 60° B . 75° C . 87° D . 120°

答案解析收藏纠错 + 选题

二、填空题

16. (2022·徐州模拟) 如图，已知每个小方格的边长均为1，则 $\text{[math]}$ 与 $\text{[math]}$ 的周长比为．

答案解析收藏纠错 + 选题
17. (2021·昭通模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P是 $\text{[math]}$ 边的中点，点Q是 $\text{[math]}$ 边上一动点，若 $\text{[math]}$ 与 $\text{[math]}$ 相似，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
18. (2022·双辽模拟) 如图，正方形纸片ABCD的边长为12，点F是AD上一点，将 $\text{[math]}$ 沿CF折叠，点D落在点G处，连接DG并延长交AB于点E ．若 $\text{[math]}$ ，则GE的长为．

答案解析收藏纠错 + 选题
19. (2023·兰山模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点B作 $\text{[math]}$ ，垂足为B ，且 $\text{[math]}$ ，连接CD ，与AB相交于点M ，过点M作 $\text{[math]}$ ，垂足为N ．若 $\text{[math]}$ ，则MN的长为．

答案解析收藏纠错 + 选题
20. (2021九上·阳城期末) 如图，在 $\text{[math]}$ 中，点D ， E分别是 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 相交于点F ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
21. (2021·上海) 如图，已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2021·菏泽) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 均为正方形，且点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都在 $\text{[math]}$ 的边上，那么 $\text{[math]}$ 与四边形 $\text{[math]}$ 的面积比为．

答案解析收藏纠错 + 选题
23. (2021·南充) 如图，在 $\text{[math]}$ 中，D为BC上一点， $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
24. (2021九下·兴化月考) 已知两个相似三角形的相似比为4：9，那么这两个三角形的周长之比为.

答案解析收藏纠错 + 选题
25. (2021九下·咸宁月考) 如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上，若幻灯片到光源的距离为20 cm，到屏幕的距离为120 cm，且幻灯片中的图形的高度为8 cm，则屏幕上图形的高度为cm.

答案解析收藏纠错 + 选题

三、作图题

26. (2023九上·西安期末) 如图，在 $\text{[math]}$ 中，请用尺规作图法，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，使 $\text{[math]}$ .（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
27. (2021九上·渭滨期末) 尺规作图：已知点D为△ABC的边AB的中点，用尺规在△ABC的边AC上找一点E，使 $\text{[math]}$ （保留作图痕迹，不写作法）.

答案解析收藏纠错 + 选题
28. (2021九上·莲湖期末) 如图，在△ABC中，AD是角平分线，请用尺规作图法，求作△ADE，使得△ABD∼△ADE，且点D与E对应，点E在AC上.（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题

四、解答题

29. (2021·嘉定模拟) 清朝《数理精蕴》里有一首小诗《古色古香方城池》：今有一座古方城，四面正中都开门，南门直行八里止，脚下有座塔耸立．又出西门二里停，切城角恰见塔形，请问诸君能算者，方城每边长是几？
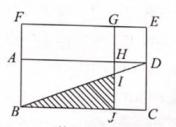
如图所示，诗的意思是：有正方形的城池一座，四面城墙的正中有门，从南门口（点D）直行8里有一塔（点A），自西门（点E）直行2里至点B，切城角（点C）也可以看见塔，问这座方城每面城墙的长是多少里？

答案解析收藏纠错 + 选题
30. (2021·韩城模拟) 青龙寺是西安最著名的櫻花观赏地，品种达到了13种之多，每年3、4月陆续开放的櫻花让这里成为了花的海洋.一天，小明和小刚去青龙寺游玩，想利用所学知识测量一棵樱花树的高度（櫻花树四周被围起来了，底部不易到达）.小明在F处竖立了一根标杆 $\text{[math]}$ ，小刚走到C处时，站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 $\text{[math]}$ 米；然后，小刚在C处蹲下，小明平移标杆到H处时，小刚恰好看到标杆顶端G和树的顶端B在一条直线上，此时测得小刚的眼睛到地面的距离 $\text{[math]}$ 米.已知 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，点C、F、H、A在一条直线上，点M在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .根据以上测量过程及测量数据，请你求出这棵樱花树 $\text{[math]}$ 的高度.

答案解析收藏纠错 + 选题
31. (2021九上·本溪期中) 九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下：如图，小卓在小越和旗杆之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小卓看着镜面上的标记，他来回走动，走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合，这时测得小卓眼睛与地面的高度ED＝1.5米，CD＝1米，然后在阳光下，小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合，测得FG＝1.6米，FH＝3.2米，已知AB⊥BM，ED⊥BM，GF⊥BM若测量时所使用的平面镜的厚度忽略不计，请你根据图中提供的相关信息求出旗杆的高AB.

答案解析收藏纠错 + 选题
32. (2021·江西模拟) 如图，D是△ABC的BC边上一点，E为AD上一点，若∠DAC=∠B，CD=CE，试说明△ACE∽△BAD．

答案解析收藏纠错 + 选题
33. (2021八下·龙泉驿期末) 小刚和小亮想用测量工具和几何知识测量公园古树 $\text{[math]}$ 的高度，由于有围栏保护，他们无法到达底部 $\text{[math]}$ ，如图，围栏 $\text{[math]}$ 米，小刚在 $\text{[math]}$ 延长线 $\text{[math]}$ 点放一平面镜，镜子不动，当小刚走到点 $\text{[math]}$ 时，恰好可以通过镜子看到树顶 $\text{[math]}$ ，这时小刚眼睛 $\text{[math]}$ 与地面的高度 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米；同时，小亮在 $\text{[math]}$ 的延长线上的 $\text{[math]}$ 处安装了测倾器（测倾器的高度忽略不计），测得树顶 $\text{[math]}$ 的仰角 $\text{[math]}$ ， $\text{[math]}$ 米，请根据题中提供的相关信息，求出古树 $\text{[math]}$ 的高度.

答案解析收藏纠错 + 选题

五、综合题

34. (2021·淮南模拟) 已知：如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，点F在边AB上，BC²＝BF•BA，CF与DE相交于点G．
1. （1）求证：△BCF∽△DGF；
2. （2）求证：DF•AB＝BC•DG；
3. （3）当点E为AC中点时，求证：2DF•EG＝AF•DG．
答案解析收藏纠错 + 选题
35. (2021·下城模拟) 如图，在△ABC中，AD是角平分线，点E ，点F分别在线段AB ， AD上，且∠EFD＝∠BDF ．
1. （1）求证：△AFE∽△ADC ．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，且∠AFE＝∠C ，探索BE和DF之间的数量关系．
答案解析收藏纠错 + 选题
36. (2021九上·四川月考) 在矩形ABCD中，E为DC边上一点，把 $\text{[math]}$ 沿AE翻折，使点D恰好落在BC边上的点F ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若AB＝2 $\text{[math]}$ ，AD＝4，求EC的长．
答案解析收藏纠错 + 选题
37. (2021·姑苏模拟) 如图，四边形 $\text{[math]}$ 是矩形，点E是边 $\text{[math]}$ 上一点， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2） F为 $\text{[math]}$ 延长线上一点，满足 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G ．若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
38. (2021九下·千山期中) 在四边形 ABCD 中，BD 平分∠ABC．
1. （1）如图 1，若∠BAD=∠BDC，求证：BD²=AB•BC；
2. （2）如图2，∠A>90°，∠BAD+∠BDC=180°，
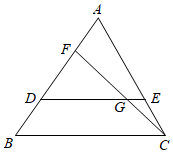
  ①若∠ABC=90°，AB= $\text{[math]}$ ，BC=8，求BD的长；
  
  ②若BC=3CD=3a，BD=9，则 AB 的长为 ▲ ．（用含 a 的代数式表示）．
答案解析收藏纠错 + 选题
39. (2021·南海模拟) 如图，圆内接正方形 $\text{[math]}$ 是圆弧 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ，线段 $\text{[math]}$ 上有一点 $\text{[math]}$ ，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）连接 $\text{[math]}$ ，当四边形 $\text{[math]}$ 是平行四边形时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
40. (2019九上·太原期中) 方格图中的每个小方格都是边长为1小正方形，我们把小正方形的顶点称为格点，格点连线为边的四边形称为“格点四边形”，图1中的四边形ABCD就是一个格点四边形.
1. （1）小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答：四边形ABCD与四边形EFGH相似吗？若相似，直接写出四边形ABCD与四边形EFGH的相似比；若不相似说明理由；
2. （2）请在图3的方格图中画一个格点四边形，使它与四边形ABCD相似，但与四边形ABCD、四边形EFGH都不全等.
答案解析收藏纠错 + 选题