


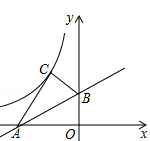

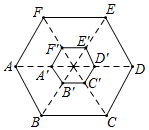

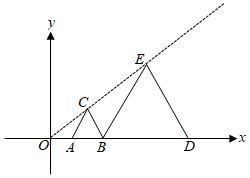
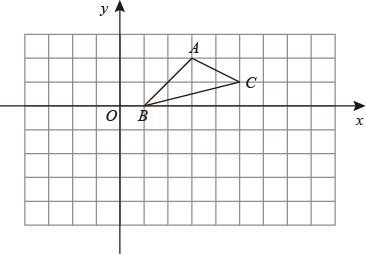
( 1 )将 向左平移5个单位长度,得到
,画出
;
( 2 )以点 为位似中心,将
放大到两倍(即新图与原图的相似比为2),得到
,在所给的方格纸中画出
;
( 3 )若点 是
的中点,经过(1)、(2)两次变换,
的对应点
的坐标是 .
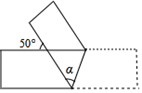
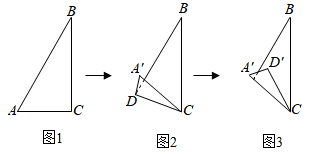
①当折叠后 与
重叠部分的图形为三角形时,请写出
与
的函数关系式,并直接写出
的取值范围;
②当重叠部分面积最大时,把 绕点
旋转,得到
,点
的对应点分别为
,连接
,求
面积的最大值(直接写出结果即可).
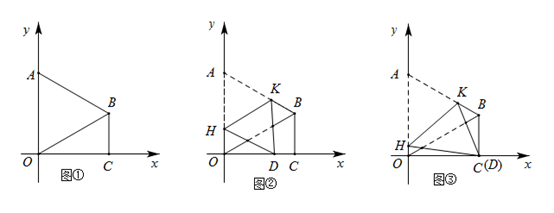
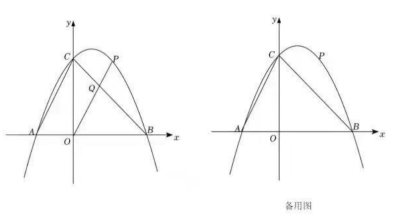
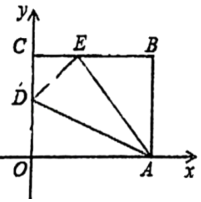
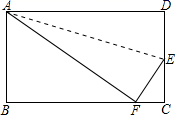
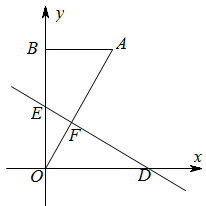
(Ⅰ)如图①,若点 坐标为
,求
的长;
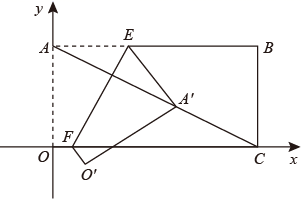
(Ⅱ)如图②,将四边形 折叠,使点
落在线段
上的点为点
,
为折痕,点
在
上,点
在
上,且使
轴.
①试判断四边形 的形状,并证明你的结论;
②求 的值;
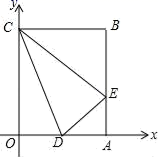
(Ⅲ)如图③,将四边形 折叠,使点
落在线段
上的点
与
点重合,
为折痕,点
在
上,点
在
上,求
的值(直接写出结果即可).