2022年江苏省连云港市中考数学模拟卷1

更新时间：2022-04-27 浏览次数：163 类型：中考模拟

一、选择题（每题3分，共24分）

1. (2022九下·江津期中) -7的相反数是（）

A . -7 B . $\text{[math]}$ C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题
2. (2022九下·湖南期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·大庆模拟) 近年来，国家高度重视精准扶贫，收效显著．据不完全统计6年间全国约有82000000人脱贫．数字82000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·珠海模拟) 如果一个正多边形的内角和是900°，则这个正多边形是（）

A . 正七边形 B . 正九边形 C . 正五边形 D . 正十边形

答案解析收藏纠错 + 选题
5. (2022·亳州模拟) 将一对直角三角板如图放置，点C在 $\text{[math]}$ 的延长线上，点B在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·重庆模拟) 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的边 $\text{[math]}$ 在x轴的正半轴上，反比例函数 $\text{[math]}$ 的图象经过对角线 $\text{[math]}$ 的中点D和顶点C若菱形 $\text{[math]}$ 的面积为9，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·合肥模拟) 如图， $\text{[math]}$ ， AC与BD交于点O，过点O作 $\text{[math]}$ ，分别交AB，CD于点E，F，则下列结论不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·交城模拟) 如图，正方形ABCD的边长是 $\text{[math]}$ ，以正方形对角线的一半OA为边作正六边形，其中一边与正方形的边CD交于点E，再以点O为圆心OE为半径画弧交AD于点F，则图中阴影部分的的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共24分）

9. (2021九上·长沙期末) 从2022年起长沙市学校体育中考增加素质类选测项目：立定跳远和1分钟跳绳.小熙选择了1分钟跳绳项目，她10次跳绳训练的成绩为140，155，142，155，166，167，166，170，180，176，这组数据的中位数是.

答案解析收藏纠错 + 选题
10. (2020八上·榆次期中) $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2021九上·长沙月考) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022·凤阳模拟) 已知关于x的方程x²－3x＋k＝0有两个不相等的实数根，则k的取值范围是

答案解析收藏纠错 + 选题
13. (2022·朝阳模拟) 已知如图，在 $\text{[math]}$ ABC中， $\text{[math]}$ BAE= $\text{[math]}$ CAE，BE $\text{[math]}$ AE于点E，若 $\text{[math]}$ ABC=3 $\text{[math]}$ ACB，则AB，AC，BE之间的数量关系．

答案解析收藏纠错 + 选题
14. (2022·烟台模拟) 如图，线段 $\text{[math]}$ ，用尺规作图法按如下步骤作图．
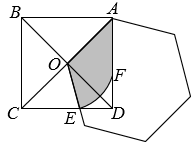
⑴过点B作 $\text{[math]}$ 的垂线，并在垂线上取 $\text{[math]}$ ；
⑵连接 $\text{[math]}$ ，以点C为圆心， $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点E；
⑶以点A为圆心， $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点D．即点D为线段 $\text{[math]}$ 的黄金分割点．
则线段 $\text{[math]}$ 的长度约为 $\text{[math]}$ （结果保留两位小数，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
15. (2021九上·平谷期末) 某地的药材批发公司指导农民养植和销售某种药材，经市场调研发现1-8月份这种药材售价（元）与月份之间存在如下表所示的一次函数关系，同时，每千克的成本价（元）与月份之间近似满足如图所示的抛物线，观察两幅图表，试判断月份出售这种药材获利最大．
月份
...
3
6
...
每千克售价
...
8
6
...

答案解析收藏纠错 + 选题
16. (2022九下·锦江开学考) 在平面直角坐标系xOy中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，其中 $\text{[math]}$ ，函数 $\text{[math]}$ 的图象分别与线段BC，AC交于点P，Q.若 $\text{[math]}$ ，则t的值为.

答案解析收藏纠错 + 选题

三、解答题（共11题，共102分）

17. (2022·朝阳模拟) 计算：（﹣1）²⁰²⁰﹣ $\text{[math]}$ ﹣（3﹣π）⁰+|3﹣ $\text{[math]}$ |+（tan30°）^﹣¹ ．

答案解析收藏纠错 + 选题
18. (2022·安徽模拟) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2022八下·长沙开学考) 解分式方程： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2022·瑞金模拟) 家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康．某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查．
1. （1）下列选取样本的方法最合理的一种是．（只需填上符合题意答案的序号）
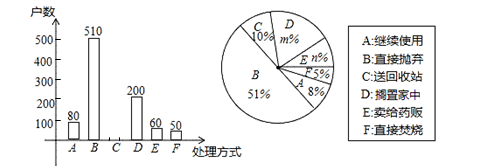
  ①在市中心某个居民区以家庭为单位随机抽取；
  ②在全市医务工作者中以家庭为单位随机抽取；
  ③在全市常住人口中以家庭为单位随机抽取．
2. （2）本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如图：
  ①m= ▲ ；n= ▲ ；
  ②补全条形统计图；
  ③根据调查数据，你认为该市市民家庭处理过期药品最常见的方式是 ▲ ；
  ④家庭过期药品的正确处理方式是送回收站点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收站点．
答案解析收藏纠错 + 选题
21. (2022·高安模拟) 根据省教育厅《关于认真做好2022年初中毕业生升学体育考试工作的通知》精神，凡报考我市普通高中、中等职业学校、五年制高职的应届、往届初中毕业生，均须参加2022年初中毕业升学体育考试，考试项目分为必考项目和选考项目，必考项目含男生1000米跑，女生800米跑；选考项目由考上从七个项目中任选2项，男生选考项目含50米跑、立定跳远、投掷实心球、引体向上、篮球运球、足球运球、排球垫球，女生选考项目含50米跑、立定跳远、一分钟仰卧起坐、引体向上、篮球运球、足球运球、排球垫球．小康决定从50米跑、立定跳远、投掷实心球（分别用A，B，C表示）选2项考试，每个项目选到的可能性相同
1. （1） “小康选到引体向上”是事件；
2. （2）请用列表或画树状图的方法，求小康选到50米跑、立定跳远的概率．
答案解析收藏纠错 + 选题
22. (2022·云南模拟) 如图，在四边形ABCD中，∠ACB＝90°， $\text{[math]}$ ，点E是AB的中点，连接EC，过点E作EF⊥AD，垂足为F，已知 $\text{[math]}$ ．
1. （1）求证：四边形AECD是菱形：
2. （2）若AB＝25，BC＝15，求线段EF的长
答案解析收藏纠错 + 选题
23. (2022九下·湖南期中) 某公司后勤部准备去超市采购牛奶和咖啡若干箱，现有两种不同的购买方案，如表：

牛奶（箱）
咖啡（箱）
金额（元）
方案一
20
10
1100
方案二
10
20
1300
1. （1）求牛奶与咖啡每箱分别为多少元；
2. （2）超市中该款咖啡和牛奶有部分因保质期临近，进行打六折的促销活动，后勤部根据需要选择原价或打折的咖啡和牛奶，此次采购共花费了1800元，其中购买打折的牛奶箱数是所有牛奶、咖啡的总箱数的 $\text{[math]}$ ，则此次按原价采购的咖啡有箱.（直接写出答案）
答案解析收藏纠错 + 选题
24. (2022·威海模拟) 如图，已知 $\text{[math]}$ ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F．
1. （1）求证：EF是⊙O的切线；
2. （2）若BF＝10，EF＝20，求⊙O的半径和AD的长．
答案解析收藏纠错 + 选题
25. (2022·瑞金模拟) 如图所示的是一款机械手臂，由上臂、中臂和底座三部分组成，其中上臂和中臂可自由转动，底座与水平地面垂直．在实际运用中要求三部分始终处于同一平面内，其示意图如图1所示，经测量，上臂 $\text{[math]}$ ，中臂 $\text{[math]}$ ，底座 $\text{[math]}$
1. （1）若上臂 $\text{[math]}$ 与水平面平行， $\text{[math]}$ ．计算点 $\text{[math]}$ 到地面的距离．
2. （2）在一次操作中，中臂与底座成 $\text{[math]}$ 夹角，上臂与中臂夹角为 $\text{[math]}$ ，如图2，计算这时点 $\text{[math]}$ 到地面的距离．与图1状态相比，这时点A向前伸长了多少?
答案解析收藏纠错 + 选题
26. (2022九下·湖南期中) 抛物线 $\text{[math]}$ 交x轴于点A，B（A在B的左边），交y轴于点C，顶点为M，对称轴MD交x轴于点D，E是线段MD上一动点，以OB，BE为邻边作平行四边形OBEF，EF交抛物线于点P，G（P在G的左边），交y轴于点H.
1. （1）求点A，B，C的坐标；
2. （2）如图1，当 $\text{[math]}$ 时，求DE的长；
3. （3）如图2，当 $\text{[math]}$ 时，
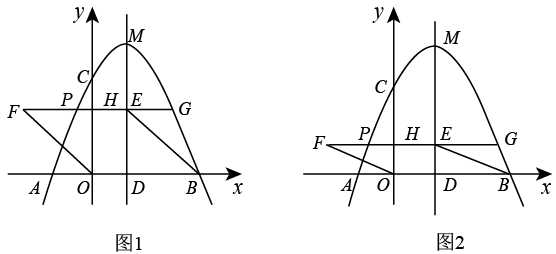
  ①求直线FC的解析式，并判断点M是否落在该直线上.
  ②连接CG，MG，CP，MP，记 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ ▲ .
答案解析收藏纠错 + 选题
27. (2022·交城模拟) 综合与实践
问题情境

Rt△ABC和Rt△DEF如图1放置，点B与点D重合，∠ACB=∠EDF=90°，∠A=30°，AB=ED=FD=4，EF分别与AC，AB交于点N，点P，点M是AB的中点．
1. （1）数学思考
  连接MN，求证：点N是EF的中点；并计算△MNP的面积；
2. （2）操作探究
  如图2，先将△DEF沿BC的方向平移，使点D与点C重合，再沿CA的方向平移到点D为AC的中点时停止；过点C作CH∥AB交DE于点H，连接AH，AN，CM．试判断四边形AMCH的形状，并说明理由；
3. （3）在图2的基础上，将△DEF绕着点D顺时针旋转30°，CH∥AB仍然存在，延长CH交MN于点G，交EF于点Q，如图3．请直接写出三角形CMG的面积．
答案解析收藏纠错 + 选题