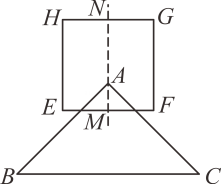
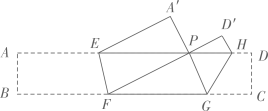
①∠AED+∠EAC+∠EDB=90°,②AP=FP , ③AE= AO , ④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,⑤CE•EF=EQ•DE .
其中正确的结论有( )
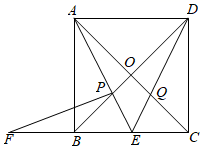




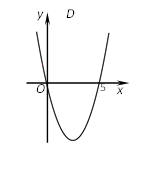
解一元二次不等式:x2-5x>0.
解:设x2-5x=0,解得:x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示).由图象可知:当x<0或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0.
所以一元二次不等式x2-5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
①转化思想;②分类讨论思想;③数形结合思想.
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想 转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.

下表是2019-2020赛季职业联赛积分榜(部分球队)
球队 | 比赛场数 | 胜场 | 负场 | 积分 |
广东东莞银行 | 30 | 28 | 2 | 58 |
新疆伊力特 | 29 | 22 | 7 | 51 |
辽宁本钢 | 30 | 20 | 10 | 50 |
山东西王 | 30 | 19 | 11 | 49 |
山西汾酒 | 30 | 18 | 12 | 48 |
福建豹发力 | 30 | 13 | 17 | 43 |
小明和小亮不仅热爱篮球,而且对联赛积分问题产生了浓厚的兴趣.他们提出的问题是:“胜一场、负一场分别积几分?”
小亮的解法是:设胜一场积x分,负一场积y分,………………………第一步
可得二元一次方程组………………………第二步
由①,得③………………………第三步
将③代入②,得………………………第四步
解这个方程,得………………………第五步
将代入③中,得
………………………第六步
解得………………………第七步
答:胜一场积2分,负一积1分.……………………第八步
任务1:将小明的思路中的空格处填起来;
A.转化思想 B.一般到特殊思想
C.分类思想 D.数形结合思想
任务3:设胜一场积x分,负一场积y分,请你选择与小明和小亮不同的等量关系,列二元一次方程组.(只列不解)
例如:已知a2+2a=2,则代数式2a2+4a+3=2(a2+2a)+3=2×2+3=7.
请你根据以上材料解答以下问题:
![]()
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?
①求2秒后,点A、B、C表示的数;
②运动t秒后,求点B和点C之间的距离(用“BC”表示)和点A和点B之间的距离(用“AB”表示);(用含t的代数式表示)
③在②的基础上,请问:3×BC-AB的值是否随着时间t的变化而变化?若不变化,求这个不变的值;若变化,求这个值的变化范围;
