2022年全国中考数学真题分类汇编23 图形的变换（2）

更新时间：2023-01-05 浏览次数：125 类型：二轮复习

一、单选题

1. (2023九下·柳州月考) 下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·东莞月考) 下列绿色能源图标中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023九上·长沙期中) 下面用数学家名字命名的图形中，既是轴对称图形，又是中心对称图形的是（）

A . 赵爽弦图 B . 笛卡尔心形线 C . 科克曲线 D . 斐波那契螺旋线

答案解析收藏纠错 + 选题
4. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的周长比是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·拱墅期中) 2022年2月第24届冬季奥林匹克运动会在我国北京成功举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2024八下·隆回期末) 在平面直角坐标系 $\text{[math]}$ 中，点A与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称，点A与点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称.已知点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·铜仁) 如图，若抛物线 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于点C，若 $\text{[math]}$ .则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九下·巧家模拟) 已知△ABC与△A₁B₁C₁是位似图形，位似比是1：3，则△ABC与△A₁B₁C₁的面积比（）

A . 1 ：3 B . 1：6 C . 1：9 D . 3：1

答案解析收藏纠错 + 选题
9. 如图，在△ABC中，D，E分别是AB和AC上的点，DE∥BC，若 $\text{[math]}$ ＝ $\text{[math]}$ ，那么 $\text{[math]}$ ＝（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·枣阳模拟) 在平面直角坐标系中，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于原点成中心对称，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 3

答案解析收藏纠错 + 选题
11. 如图， $\text{[math]}$ 相交于点E， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
12. 图中的图形为轴对称图形，该图形的对称轴的条数为（）

A . 1 B . 2 C . 3 D . 5

答案解析收藏纠错 + 选题
13. (2022·赤峰) 下列图案中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
14. (2022·赤峰) 如图，点 $\text{[math]}$ ，将线段 $\text{[math]}$ 先向上平移2个单位长度，再向左平移3个单位长度，得到线段 $\text{[math]}$ ，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2022·呼和浩特) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，使点 $\text{[math]}$ 的对应点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上， $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（用含 $\text{[math]}$ 的代数式表示）（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2022·哈尔滨) 下列图形中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
17. (2022·包头) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点C顺时针旋转得到 $\text{[math]}$ ，其中点 $\text{[math]}$ 与点A是对应点，点 $\text{[math]}$ 与点B是对应点．若点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上，则点A到直线 $\text{[math]}$ 的距离等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 2

答案解析收藏纠错 + 选题
18. (2022九上·碑林月考) 雪花、风车….展示着中心对称的美，利用中心对称，可以探索并证明图形的性质，请思考在下列图形中，是中心对称图形但不一定是轴对称图形的为（）

A . 扇形 B . 平行四边形 C . 等边三角形 D . 矩形

答案解析收藏纠错 + 选题
19. (2023·重庆市模拟) 如图，以点O为位似中心，作四边形 $\text{[math]}$ 的位似图形 $\text{[math]}$ ﹐已知 $\text{[math]}$ ，若四边形 $\text{[math]}$ 的面积是2，则四边形 $\text{[math]}$ 的面积是（）

A . 4 B . 6 C . 16 D . 18

答案解析收藏纠错 + 选题
20. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

21. (2022·衢州) 希腊数学家海伦给出了挖掘直线隧道的方法：如图，A，B是两侧山脚的入口，从B出发任作线段BC，过C作CD⊥BC，然后依次作垂线段DE，EF，FG，GH，直到接近点A，作AJ⊥GH于点J．每条线段可测量，长度如图所示．分别在BC，AJ上任选点M，N，作MQ⊥BC，NP⊥AJ，使得 $\text{[math]}$ ，此时点P，A，B，Q共线．挖隧道时始终能看见P，Q处的标志即可．
1. （1） $\text{[math]}$ km．
2. （2） $\text{[math]}$ =．
答案解析收藏纠错 + 选题
22. (2022·西宁) 如图，在△ABC中，∠C=90°，∠B=30°，AB=6，将△ABC绕点A逆时针方向旋转15°得到△AB′C′，B′C′交AB于点E，则B′E=．

答案解析收藏纠错 + 选题
23. (2022·潍坊) 《墨子·天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形 $\text{[math]}$ 的面积为4，以它的对角线的交点为位似中心，作它的位似图形 $\text{[math]}$ ，若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的外接圆的周长为．

答案解析收藏纠错 + 选题
24. (2023·遵义模拟) 如图，在四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的面积是 $\text{[math]}$ ， $\text{[math]}$ 度.

答案解析收藏纠错 + 选题
25. (2024·广西模拟) 数学兴趣小组通过测量旗杆的影长来求旗杆的高度，他们在某一时刻测得高为2米的标杆影长为1.2米，此时旗杆影长为7.2米，则旗杆的高度为米.

答案解析收藏纠错 + 选题
26. (2023·北京市模拟) 如图，在矩形 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
27. (2022·赤峰) 如图，为了测量校园内旗杆AB的高度，九年级数学应用实践小组，根据光的反射定律，利用镜子、皮尺和测角仪等工具，按以下方式进行测量：把镜子放在点O处，然后观测者沿着水平直线BO后退到点D，这时恰好能在镜子里看到旗杆顶点A，此时测得观测者观看镜子的俯角α=60°，观测者眼睛与地面距离CD=1.7m，BD=11m，则旗杆AB的高度约为m．（结果取整数， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
28. (2022·贺州) 如图，在平面直角坐标系中， $\text{[math]}$ 为等腰三角形， $\text{[math]}$ ，点B到x轴的距离为4，若将 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
29. (2022·北部湾) 古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔影子的顶部直立一根木杆，借助太阳光测金字塔的高度.如图，木杆EF长2米，它的影长FD是4米，同一时刻测得OA是268米，则金字塔的高度BO是米.

答案解析收藏纠错 + 选题

三、作图题

30. (2022·吉林) 图①，图②均是 $\text{[math]}$ 的正方形网格，每个小正方形的顶点称为格点．其中点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均在格点上．请在给定的网格中按要求画四边形．
1. （1）在图①中，找一格点 $\text{[math]}$ ，使以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是轴对称图形；
2. （2）在图②中，找一格点 $\text{[math]}$ ，使以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是中心对称图形．
答案解析收藏纠错 + 选题
31. (2022·哈尔滨) 如图，方格纸中每个小正方形的边长均为1， $\text{[math]}$ 的顶点和线段 $\text{[math]}$ 的端点均在小正方形的顶点上．
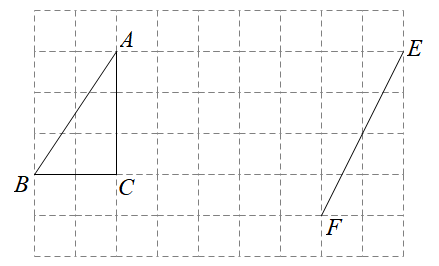
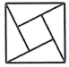
⑴在方格纸中面出 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称（点D在小正方形的顶点上）；
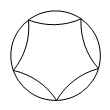
⑵在方格纸中画出以线段 $\text{[math]}$ 为一边的平行四边形 $\text{[math]}$ （点G，点H均在小正方形的顶点上），且平行四边形 $\text{[math]}$ 的面积为4．连接 $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题

四、综合题

32. (2022·攀枝花) 如图，直线 $\text{[math]}$ 分别与x轴、y轴交于点A、B，点C为线段 $\text{[math]}$ 上一动点（不与A、B重合），以C为顶点作 $\text{[math]}$ ，射线 $\text{[math]}$ 交线段 $\text{[math]}$ 于点D，将射线 $\text{[math]}$ 绕点O顺时针旋转 $\text{[math]}$ 交射线 $\text{[math]}$ 于点E，连接 $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ ；（用图1）
2. （2）当 $\text{[math]}$ 为直角三角形时，求 $\text{[math]}$ 的长度；（用图2）
3. （3）点A关于射线 $\text{[math]}$ 的对称点为F，求 $\text{[math]}$ 的最小值.（用图3）
答案解析收藏纠错 + 选题
33. (2024·阳西模拟) 已知二次函数图象的顶点坐标为 $\text{[math]}$ ，且与x轴交于点 $\text{[math]}$ ．
1. （1）求二次函数的表达式；
2. （2）如图，将二次函数图象绕x轴的正半轴上一点 $\text{[math]}$ 旋转 $\text{[math]}$ ，此时点A、B的对应点分别为点C、D．
  ①连结 $\text{[math]}$ ，当四边形 $\text{[math]}$ 为矩形时，求m的值；
  ②在①的条件下，若点M是直线 $\text{[math]}$ 上一点，原二次函数图象上是否存在一点Q，使得以点B、C、M、Q为顶点的四边形为平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
34. (2022·恩施) 在平面直角坐标系中，O为坐标原点，抛物线 $\text{[math]}$ 与y轴交于点 $\text{[math]}$ .
1. （1）直接写出抛物线的解析式.
2. （2）如图，将抛物线 $\text{[math]}$ 向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由.
3. （3）直线BC与抛物线 $\text{[math]}$ 交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与 $\text{[math]}$ 相似，若存在，请求出点T的坐标；若不存在，请说明理由.
4. （4）若将抛物线 $\text{[math]}$ 进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出拋物线 $\text{[math]}$ 平移的最短距离并求出此时抛物线的顶点坐标.
答案解析收藏纠错 + 选题
35. (2022·桂林) 如图，抛物线y＝﹣x²+3x+4与x轴交于A，B两点（点A位于点B的左侧），与y轴交于C点，抛物线的对称轴l与x轴交于点N，长为1的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动.
1. （1）直接写出A，B，C三点的坐标；
2. （2）求CP+PQ+QB的最小值；
3. （3）过点P作PM⊥y轴于点M，当 $\text{[math]}$ CPM和 $\text{[math]}$ QBN相似时，求点Q的坐标.
答案解析收藏纠错 + 选题
36. (2022·哈尔滨) 在平面直角坐标系中，点O为坐标原点，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，点 $\text{[math]}$ ，与y轴交于点C．
1. （1）求a，b的值；
2. （2）如图1，点D在该抛物线上，点D的横坐标为 $\text{[math]}$ ，过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接 $\text{[math]}$ 、设点P的纵坐标为t， $\text{[math]}$ 的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
3. （3）如图2，在（2）的条件下，连接 $\text{[math]}$ ，点F在 $\text{[math]}$ 上，过点F向y轴作垂线，垂足为点H，连接 $\text{[math]}$ 交y轴于点G，点G为 $\text{[math]}$ 的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点M，点R在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求直线 $\text{[math]}$ 的解析式．
答案解析收藏纠错 + 选题
37. (2022·无锡) 已知二次函数 $\text{[math]}$ 图象的对称轴与x轴交于点A（1，0），图象与y轴交于点B（0，3），C、D为该二次函数图象上的两个动点（点C在点D的左侧），且 $\text{[math]}$ .
1. （1）求该二次函数的表达式；
2. （2）若点C与点B重合，求tan∠CDA的值；
3. （3）点C是否存在其他的位置，使得tan∠CDA的值与（2）中所求的值相等？若存在，请求出点C的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
38. (2023·抚顺模拟) 如图，已知抛物线： $\text{[math]}$ 与x轴交于点A， $\text{[math]}$ （A在B的左侧），与y轴交于点C，对称轴是直线 $\text{[math]}$ ，P是第一象限内抛物线上的任一点．
1. （1）求抛物线的解析式；
2. （2）若点D为线段 $\text{[math]}$ 的中点，则 $\text{[math]}$ 能否是等边三角形？请说明理由；
3. （3）过点P作x轴的垂线与线段 $\text{[math]}$ 交于点M，垂足为点H，若以P，M，C为顶点的三角形与 $\text{[math]}$ 相似，求点P的坐标．
答案解析收藏纠错 + 选题
39. (2022·梧州) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 分别与x，y轴交于点A，B，抛物线 $\text{[math]}$ 恰好经过这两点.
1. （1）求此抛物线的解析式；
2. （2）若点C的坐标是 $\text{[math]}$ ，将 $\text{[math]}$ 绕着点C逆时针旋转90°得到 $\text{[math]}$ ，点A的对应点是点E.
  ①写出点E的坐标，并判断点E是否在此抛物线上；
  
  ②若点P是y轴上的任一点，求 $\text{[math]}$ 取最小值时，点P的坐标.
答案解析收藏纠错 + 选题
40. (2023·泰州模拟) 如图1，在平面直角坐标系中，Rt△OAB的直角边OA在y轴的正半轴上，且OA=6，斜边OB=10，点P为线段AB上一动点.
1. （1）请直接写出点B的坐标；
2. （2）若动点P满足∠POB=45°，求此时点P的坐标；
3. （3）如图2，若点E为线段OB的中点，连接PE，以PE为折痕，在平面内将△APE折叠，点A的对应点为A'，当PA'⊥OB时，求此时点P的坐标；
4. （4）如图3，若F为线段AO上一点，且AF=2，连接FP，将线段FP绕点F顺时针方向旋转60°得线段FG，连接OG，当OG取最小值时，请直接写出OG的最小值和此时线段FP扫过的面积.
答案解析收藏纠错 + 选题