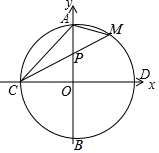

①求证: ;
②求y与x之间的函数关系式.
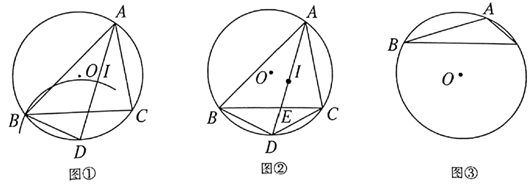
①当点D与点B重合,点P为弧AB的中点时,求证: .
②当 ,
时,求
的值.
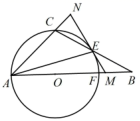

①若∠BDE=45°,求PD的长.
②若ΔBED为等腰三角形,求直接写出所有满足条件的BD的长.
①当
时,四边形
为正方形;
②当 时,四边形
为菱形.

①求证: ∽
②若 ,
的面积为
,求⊙O的半径.
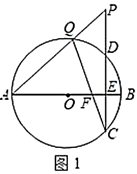
如图1,直径AB垂直弦CD于点E,AB=10,CD=8,点P是CD延长线上异于点D的一个动点,连接AP交⊙O于点Q,连接CQ交AB于点F,则点F的位置随着点P位置的改变而改变.

如图2,连接AC,DQ,在点P运动过程中,设DP=x, y.
①求证:∠ACQ=∠CPA;
②求y与x之间的函数关系式;
当OF=1时,求△ACQ和△CDQ的面积之比.(直接写出答案)