2023年中考数学探究性试题复习2 图形规律

更新时间：2023-05-22 浏览次数：134 类型：三轮冲刺

一、单选题

1. (2023·临淄模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 边上的高 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上，且四边形 $\text{[math]}$ 为正方形，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ 1， $\text{[math]}$ ， $\text{[math]}$ 上，且四边形 $\text{[math]}$ 为正方形，…按此规律操作下去，则线段 $\text{[math]}$ 的长度为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·昭通模拟) 用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑩个图案中正方形的个数为（）

A . 32 B . 33 C . 37 D . 41

答案解析收藏纠错 + 选题
3. (2023·天河模拟) 按如图所示的规律搭正方形：搭一个小正方形需要4根小棒，搭两个小正方形需要7根小棒，则搭2023个这样的小正方形需要小棒（）

A . 6068根 B . 6069根 C . 6070根 D . 6071根

答案解析收藏纠错 + 选题
4. (2023·封丘模拟) 将含有 $\text{[math]}$ 角的直角三角板 $\text{[math]}$ 按如图所示的方式放置在平面直角坐标系中， $\text{[math]}$ 在 $\text{[math]}$ 轴上，若 $\text{[math]}$ ，将角板绕原点O逆时针旋转，每秒旋转 $\text{[math]}$ ，则第2019秒时，点A的对应点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·金乡县模拟) 边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·保定开学考) 如图，在平面直角坐标系中，将边长为2的正六边形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 个 $\text{[math]}$ ，得到正六边形 $\text{[math]}$ ，当 $\text{[math]}$ 时，正六边形 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022七上·阳西期末) 如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）

A . 297 B . 301 C . 303 D . 400

答案解析收藏纠错 + 选题
8. (2023八下·盐城月考) 如图，已知矩形ABCD的边长分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形 $\text{[math]}$ ；第二次，顺次连接四边形 $\text{[math]}$ 各边的中点，得到四边形 $\text{[math]}$ ；…如此反复操作下去，则第n次操作后，得到四边形 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·重庆市模拟) 把菱形按照如图所示的规律拼图案，其中第①个图案中有 1个菱形，第②个图案中有 3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）

A . 15 B . 13 C . 11 D . 9

答案解析收藏纠错 + 选题
10. (2022七下·重庆开学考) 如图，小明用棋子摆了几个“开”字，其中第①个“开”字用了14个棋子，第②个“开”字用了20个棋子，第③个“开”字用了26个棋子…，照此规律继续摆下去，第7个图需用到的棋子数为（）

A . 38 B . 44 C . 50 D . 56

答案解析收藏纠错 + 选题

二、填空题

11. (2023·原平模拟) 如图所示的是一组有规律的图案，则第n个图案中“”的个数为．（用含n的代数式表示）

答案解析收藏纠错 + 选题
12. (2023·城阳模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D、点E、点F分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 边的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，得到 $\text{[math]}$ ，它的面积记作S；点 $\text{[math]}$ 、点 $\text{[math]}$ 、点 $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 边的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，得到 $\text{[math]}$ ，它的面积记作 $\text{[math]}$ ，照此规律作下去，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023八下·齐齐哈尔期中) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 与直线l所夹锐角为 $\text{[math]}$ ，延长 $\text{[math]}$ 交直线l于点 $\text{[math]}$ ，作正方形 $\text{[math]}$ ，延长 $\text{[math]}$ 交直线l于点 $\text{[math]}$ ，作正方形 $\text{[math]}$ ，延长 $\text{[math]}$ 交直线l于点 $\text{[math]}$ ，作正方形 $\text{[math]}$ ， …，依此规律，则线段 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023·龙江模拟) 如图，正方形 $\text{[math]}$ 的中心与坐标原点O重合，将顶点 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得点 $\text{[math]}$ ，再将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得点 $\text{[math]}$ ，再将 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ 得点 $\text{[math]}$ ，再将 $\text{[math]}$ 绕点D逆时针旋转 $\text{[math]}$ 得点 $\text{[math]}$ ，再将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得点 $\text{[math]}$ ……依此类推，则点 $\text{[math]}$ 的坐标是.

答案解析收藏纠错 + 选题
15. (2023·包头模拟) 在直角坐标系中，等腰直角三角形 $\text{[math]}$ 按如图所示的方式放置，其中点 $\text{[math]}$ 均在一次函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 均在x轴上．若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
16. (2023·绥化模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为菱形 $\text{[math]}$ 各边的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 得四边形 $\text{[math]}$ ，以此类推得四边形 $\text{[math]}$ ……若菱形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
17. (2023·宾阳模拟) 在平面直角坐标系 $\text{[math]}$ 中，记直线 $\text{[math]}$ 为l.点 $\text{[math]}$ 是直线l与y轴的交点，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，使点 $\text{[math]}$ 落在x轴正半轴上，作射线 $\text{[math]}$ 交直线l于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，使点 $\text{[math]}$ 落在x轴正半轴上，依次作下去，得到如图所示的图形.则点 $\text{[math]}$ 的坐标是.

答案解析收藏纠错 + 选题
18. (2023·内江模拟) 如图，点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第2023次运动后动点P的坐标是 .

答案解析收藏纠错 + 选题
19. (2023·太谷模拟) 某公园内有一矩形步道，其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式，其中步道上总共使用84个三角形地砖，那么连续排列的正方形地砖总共有个．

答案解析收藏纠错 + 选题
20. (2023·鄱阳模拟) 如图所示的是由一些火柴棒摆成的图案：摆第1个图案用了5根火柴，摆第2个图案用了9根火柴，摆第3个图案用了13根火柴……按照这种方式摆下去，摆第10个图案需要用的火柴棒根数是．

答案解析收藏纠错 + 选题
21. (2022·锦州) 如图， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点， $\text{[math]}$ ．以 $\text{[math]}$ 为边在其右侧作菱形A₁B₁C₁D₁ ，且 $\text{[math]}$ 与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ，得 $\text{[math]}$ ；延长 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边在其右侧作菱形 $\text{[math]}$ ，且 $\text{[math]}$ 与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ，得 $\text{[math]}$ ；延长 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边在其右侧作菱形 $\text{[math]}$ ，且 $\text{[math]}$ 与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ，得 $\text{[math]}$ ；…，按此规律进行下去，则 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
22. (2022·黔西) 如图，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点为 $\text{[math]}$ ；…；按此做法进行下去，则点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
23. (2023九上·邳州期末) 《庄子▪天下篇》记载“一尺之锤，日取其半，万世不竭．”如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，以此类推，令 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 对任意大于1的整数 $\text{[math]}$ 恒成立，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题

三、综合题

24. (2023·全椒模拟) 在美术课上，小明设计如图所示的图案，每个图案都是由白点和黑点组成，归纳图案中的规律，完成下列问题．
1. （1）在图5中，白点有个，黑点有个；图 $\text{[math]}$ 中，白点有个，黑点有个；
2. （2）在图 $\text{[math]}$ 中，若白点和黑点共有169个，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
25. (2023·来安模拟) 如图，小明设计如下的正方形图案，外一层是空心圆，内部全是实心圆，归纳图案中的规律，完成下列任务．
1. （1）图案4中，空心圆有个；图案 $\text{[math]}$ 中实心圆有个时，空心圆有个；
2. （2）此类图案中是否存在实心圆比空心圆多8个，请你作出判断并说明理由．
答案解析收藏纠错 + 选题
26. (2023·亳州模拟) 如图，下列图案都是由同样大小的基本图形 $\text{[math]}$ 按一定规律所组成的，其中：
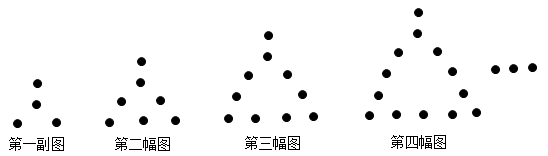
第1个图案中基本图形的个数： $\text{[math]}$ ，
第2个图案中基本图形的个数： $\text{[math]}$ ，
第3个图案中基本图形的个数： $\text{[math]}$ ，
第4个图案中基本图形的个数： $\text{[math]}$ ，
…
按此规律排列，解决下列问题：
1. （1）写出第5个图案中基本图形的个数：＝；
2. （2）如果第n个图案中有2024个基本图形，求n的值．
答案解析收藏纠错 + 选题
27. (2023·太和模拟) 为了提高动手操作能力，安徽某学校九年级学生利用课后服务时间进行拼图大赛，他们用边长相同的正方形和正三角形进行拼接，赛后整理发现一组有规律的图案，如图所示．
【观察思考】
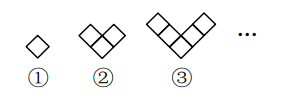
第1个图案有4个正三角形，第2个图案有7个正三角形，第3个图案有10个正三角形，…依此类推
【规律总结】
1. （1）第5个图案有个正三角形
2. （2）第n个图案中有个正三角形，（用含n的代数式表示）
3. （3）【问题解决】
  现有2023个正三角形，若按此规律拼第n个图案，要求正三角形一次用完，则该图案需要正方形多少个？
答案解析收藏纠错 + 选题
28. (2023·秦皇岛模拟) 为迎接七一建党节，某社区党委在广场上设计了一座三角形展台，需在它的每条边上摆放上相等盆数的鲜花进行装饰．若每条边上摆放两盆鲜花，共需要3盆鲜花；若每条边上摆放3盆鲜花，共需要6盆鲜花；……，按此要求摆放下去（如图所示，每个小圆圈表示一盆鲜花）．
1. （1）填写下表：
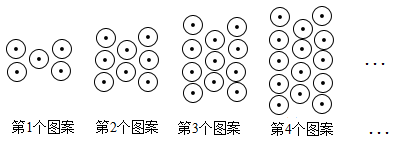
  每条边上摆放的盆数（n）
  2
  3
  4
  5
  6
  …
  需要的鲜花总盆数（y）
  3
  6
  9
  …
2. （2）写出需要的鲜花总盆数y与n之间的关系式：
3. （3）能否用2023盆鲜花作出符合要求的摆放？如果能，请计算出每条边上应摆放的盆数；如果不能，请说明理由．
答案解析收藏纠错 + 选题