2023年中考数学探究性试题复习12 二次函数-在线组卷

1. (2023·深圳模拟) 在平面直角坐标系中，如果一个点的横坐标与纵坐标相等，则称该点为“不动点”

例如 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都是“不动点”，已知双曲线 $\text{[math]}$

（1）下列说法错误的是（）

A . 直线 $\text{[math]}$ 的图象上有无数个“不动点” B . 函数 $\text{[math]}$ 的图象上没有“不动点” C . 直线 $\text{[math]}$ 的图象上有无数个“不动点” D . 函数 $\text{[math]}$ 的图象上有两个“不动点”
（2）求双曲线 $\text{[math]}$ 上的“不动点”；
（3）若抛物线 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 为常数）上有且只有一个“不动点”，
①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围．
②如果 $\text{[math]}$ ，过双曲线 $\text{[math]}$ 图象上第一象限的“不动点”作平行于 $\text{[math]}$ 轴的直线 $\text{[math]}$ ，若抛物线上有四个点到 $\text{[math]}$ 的距离为 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的取值范围．

2. (2023·原平模拟) 综合与探究．

如图1，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ ，且与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C，连接 $\text{[math]}$ ， $\text{[math]}$ ．

（1）求抛物线的表达式．
（2）求证： $\text{[math]}$ ．
（3）如图2，动点P从点B出发，沿着线段 $\text{[math]}$ 以每秒1个单位长度的速度向终点A运动；同时，动点Q从点A出发，以相同的速度沿着线段 $\text{[math]}$ 向终点C运动，当其中一个动点到达终点时，另一个动点也随之停止运动，连接 $\text{[math]}$ ，设P，Q运动的时间为t秒，在点P，Q运动的过程中， $\text{[math]}$ 是否成为等腰三角形？若能，请求出t的值；若不能，请说明理由．

答案解析收藏纠错 + 选题

3. (2023·开江模拟) 定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”，例如：点 $\text{[math]}$ 是函数 $\text{[math]}$ 的图像的“等值点”.

（1）分别判断函数 $\text{[math]}$ ， $\text{[math]}$ 的图像上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；
（2）设函数 $\text{[math]}$ ， $\text{[math]}$ 的图像的“等值点”分别为点 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，垂足为 $\text{[math]}$ .当 $\text{[math]}$ 的面积为3时，求 $\text{[math]}$ 的值；
（3）若函数 $\text{[math]}$ 的图像记为 $\text{[math]}$ ，将其沿直线 $\text{[math]}$ 翻折后的图像记为 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 两部分组成的图像上恰有2个“等值点”时，直接写出 $\text{[math]}$ 的取值范围.

答案解析收藏纠错 + 选题

4. (2023九下·盐都月考) 如图1，对于平面上小于或等于 $\text{[math]}$ 的 $\text{[math]}$ ，我们给出如下定义：若点P在 $\text{[math]}$ 的内部或边上，作 $\text{[math]}$ 于点E， $\text{[math]}$ 于点F，则将 $\text{[math]}$ 称为点P与 $\text{[math]}$ 的“点角距”，记作 $\text{[math]}$ .如图2，在平面直角坐标系 $\text{[math]}$ 中，x、y正半轴所组成的角记为 $\text{[math]}$ .

（1）已知点 $\text{[math]}$ 、点 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ .
（2）若点P为 $\text{[math]}$ 内部或边上的动点，且满足 $\text{[math]}$ ，在图2中画出点P运动所形成的图形.
（3）如图3与图4，在平面直角坐标系 $\text{[math]}$ 中，射线 $\text{[math]}$ 的函数关系式为 $\text{[math]}$ .
①在图3中，点C的坐标为 $\text{[math]}$ ，试求 $\text{[math]}$ 的值；

②在图4中，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ，与射线 $\text{[math]}$ 交于点D，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求c的值和当 $\text{[math]}$ 取最大值时点Q的坐标.

答案解析收藏纠错 + 选题

5. (2023·青海模拟) 如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法： $\text{[math]}$ ，即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题：

如图2，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B.

（1）求抛物线和直线AB的解析式；
（2）点P是抛物线(在第一象限内)上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及 $\text{[math]}$ ；
（3）是否存在一点P，使S_△PAB= $\text{[math]}$ S_△CAB，若存在，求出P点的坐标；若不存在，请说明理由.

答案解析收藏纠错 + 选题

6. (2023·寻乌模拟) 定义：若直线 $\text{[math]}$ 与开口向下的抛物线有两个交点，则这两个交点之间的距离叫做这条抛物线的“反碟长”．如图，已知抛物线 $\text{[math]}$ ： $\text{[math]}$ 与直线 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ ．

（1）抛物线 $\text{[math]}$ 的“反碟长” $\text{[math]}$ ．
（2）抛物线随其顶点沿直线 $\text{[math]}$ 向上平移，得到抛物线 $\text{[math]}$ ．
①当抛物线 $\text{[math]}$ 的顶点平移到点 $\text{[math]}$ ，抛物线 $\text{[math]}$ 的解析式是 ▲ ．抛物线 $\text{[math]}$ 的“反碟长”是 ▲ ．
②若抛物线 $\text{[math]}$ 的“反碟长”是一个偶数，则其顶点的纵坐标可能是 ▲ ．（填写所有正确的选项）
A.15 B.16 C.24 D.25
③当抛物线 $\text{[math]}$ 的顶点 $\text{[math]}$ 和抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 的两个交点 $\text{[math]}$ ， $\text{[math]}$ 构成一个等边三角形时（点 $\text{[math]}$ 在点 $\text{[math]}$ 左右），求点 $\text{[math]}$ 的坐标．

答案解析收藏纠错 + 选题

7. (2023·增城模拟) 综合与探究

已知抛物线 $\text{[math]}$ ．

（1）当抛物线经过 $\text{[math]}$ 和 $\text{[math]}$ 两点时，求抛物线的函数表达式．
（2）当 $\text{[math]}$ 时，无论a为何值，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 相交所得的线段 $\text{[math]}$ （点A在点 B的左侧）的长度始终不变，求m的值和线段 $\text{[math]}$ 的长．
（3）在（2）的条件下，将抛物线 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折得到抛物线 $\text{[math]}$ ，抛物线 $\text{[math]}$ ， $\text{[math]}$ 的顶点分别记为G，H．是否存在实数a使得以A，B，G，H为顶点的四边形为正方形？若存在，直接写出a的值；若不存在，请说明理由．

答案解析收藏纠错 + 选题

8. (2023·亳州模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 与y轴交于点C，点A的坐标为 $\text{[math]}$ ．

（1）求b的值和点B，C的坐标；
（2）若点D为 $\text{[math]}$ 的中点，点P为第一象限内抛物线上的一点，过点P作 $\text{[math]}$ 轴，垂足为H， $\text{[math]}$ 与 $\text{[math]}$ 分别交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，求点P的坐标；
（3）若直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ 两点，且有一个交点在第一象限，其中 $\text{[math]}$ ，若 $\text{[math]}$ 结合函数图象，探究n的取值范围．

答案解析收藏纠错 + 选题

9. (2023·吴兴模拟) 一张矩形纸片ABCD（如图1），AB=6，AD=3.点E是BC边上的一个动点，将△ABE沿直线AE折叠得到△AEF，延长AE交直线CD于点G，直线AF与直线CD交于点Q.

【初步探究】

（1）求证：△AQG是等腰三角形；
（2）记FQ=m，当BE=2CE时，计算m的值；
（3）【深入探究】
将矩形纸片放入平面直角坐标系中（如图2所示），点B与点O重合，边OC、OA分别与x轴、y轴正半轴重合.点H在OC边上，将△AOH沿直线AH折叠得到△APH.
①当AP经过CD的中点N时，求点P的坐标；
②在①的条件下，已知二次函数y=-x²+bx+c的图象经过A、D两点.若将直线AH右侧的抛物线沿AH对折，交y轴于点M，请求出AM的长度.

答案解析收藏纠错 + 选题

10. (2023九下·靖江期中) 定义：两个二次项系数之和为 $\text{[math]}$ ，对称轴相同，且图像与y轴交点也相同的二次函数互为友好同轴二次函数.例如： $\text{[math]}$ 的友好同轴二次函数为 $\text{[math]}$ .

（1）函数 $\text{[math]}$ 的友好同轴二次函数为.
（2）当 $\text{[math]}$ 时，函数 $\text{[math]}$ $\text{[math]}$ 的友好同轴二次函数有最大值为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
（3）已知点 $\text{[math]}$ 分别在二次函数 $\text{[math]}$ 及其友好同轴二次函数 $\text{[math]}$ 的图像上，比较 $\text{[math]}$ 的大小，并说明理由.

答案解析收藏纠错 + 选题

11. (2023·金华模拟) 如图1，在平面直角坐标系中，四边形AOBC为矩形，BC= $\text{[math]}$ ， ∠BOC=60°，D为BC中点.某反比例函数过点D，且与直线OC交于点E.

（1）点E的坐标为.
（2）好奇的小明在探索一个新函数.若点P为x轴上一点，过点P作x轴的垂线交直线AC于点Q，交该反比例函数图象于点R.若y′=PQ+PR，点P横坐标为x. $\text{[math]}$ 关于x的图像如图2，其中图像最低点F、G横坐标分别为（ $\text{[math]}$ ， $\text{[math]}$ ）、（ $\text{[math]}$ ， $\text{[math]}$ ）.
①求 $\text{[math]}$ 与x之间的函数关系式.
②写出该函数的两条性质.
（3）已知1<x<4
①若关于x的方程x²－4x－m=0有解，求m的取值范围.小明思考过程如下：由x²－4x－m=0得m=x²－4x，m是关于x的二次函数，根据x的范围可以求出m的取值范围.请你完成解题过程.
②若关于x的方程 $\text{[math]}$ 有解，请直接写出m的取值范围.

答案解析收藏纠错 + 选题

12. (2023·柳州模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与y轴交于点C，点D是抛物线的顶点.

（1）求抛物线解析式；
（2）求开口向下的二次函数的最大值时采用的步骤是：第一，求出二次函数的顶点坐标 $\text{[math]}$ ；第二，确定自变量x的取值范围；第三判定 $\text{[math]}$ 是否在其范围内，若在，则最大值是顶点纵坐标，若不在，要根据其增减性求最大值，即当 $\text{[math]}$ 时， $\text{[math]}$ 时，y最大；当 $\text{[math]}$ $\text{[math]}$ 时， $\text{[math]}$ 时，y最大.若 $\text{[math]}$ ， $\text{[math]}$ 时，二次函数 $\text{[math]}$ 的最大值是t，求t的值.
（3）如图，若点P是第一象限抛物线上一点，且 $\text{[math]}$ ，求点P的坐标.

答案解析收藏纠错 + 选题

13. (2022·安顺) 在平面直角坐标系中，如果点 $\text{[math]}$ 的横坐标和纵坐标相等，则称点 $\text{[math]}$ 为和谐点，例如：点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， ……都是和谐点．

（1）判断函数 $\text{[math]}$ 的图象上是否存在和谐点，若存在，求出其和谐点的坐标；
（2）若二次函数 $\text{[math]}$ 的图象上有且只有一个和谐点 $\text{[math]}$ ．
①求 $\text{[math]}$ ， $\text{[math]}$ 的值；

②若 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为－1，最大值为3，求实数 $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题

14. (2022·威海) 探索发现

（1）在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣3，0），B（1，0），与y轴交于点C，顶点为点D，连接AD．
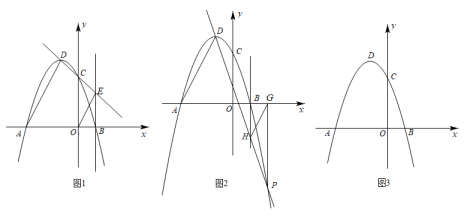
①如图1，直线DC交直线x＝1于点E，连接OE．求证：AD∥OE；
②如图2，点P（2，﹣5）为抛物线y＝ax²+bx+3（a≠0）上一点，过点P作PG⊥x轴，垂足为点G．直线DP交直线x＝1于点H，连接HG．求证：AD∥HG；
（2）通过上述两种特殊情况的证明，你是否有所发现？请仿照（1）写出你的猜想，并在图3上画出草图．在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣3，0），B（1，0），顶点为点D．点M为该抛物线上一动点（不与点A，B，D重合），
猜想：作MN⊥x轴于N，直线DM交直线x=1于Q，则QN∥AD，证明见解析

答案解析收藏纠错 + 选题

15. (2022·盐城) 【发现问题】

小明在练习簿的横线上取点 $\text{[math]}$ 为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律．

【提出问题】

小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图象上．

（1）【分析问题】
小明利用已学知识和经验，以圆心 $\text{[math]}$ 为原点，过点 $\text{[math]}$ 的横线所在直线为 $\text{[math]}$ 轴，过点 $\text{[math]}$ 且垂直于横线的直线为 $\text{[math]}$ 轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示．当所描的点在半径为5的同心圆上时，其坐标为．
（2）【解决问题】
请帮助小明验证他的猜想是否成立．
（3）【深度思考】
小明继续思考：设点 $\text{[math]}$ ， $\text{[math]}$ 为正整数，以 $\text{[math]}$ 为直径画 $\text{[math]}$ ，是否存在所描的点在 $\text{[math]}$ 上．若存在，求 $\text{[math]}$ 的值；若不存在，说明理由．

答案解析收藏纠错 + 选题

小学

初中

高中

2023年中考数学探究性试题复习12 二次函数

副标题：

*注意事项：

2023年中考数学探究性试题复习12 二次函数

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析