![]()
①点B表示的数为 (用含t的式子表示);
②是否存在t,使得此时点A关于点B的“伴侣点”P恰好与原点重合?若存在,请求出t的值;若不存在,请说明理由.
例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“和谐点”.
![]()
①若点P在点B的左侧,且点P是点A,B的“和谐点”,求出此时点P表示的数;
②若点P在点B的右侧,点P,A,B中,有一个点恰好是其它两个点的“和谐点”,求出此时点P表示的数.

如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2.数所表示的点是【M,N】的好点;
![]()

![]()

①当P点第一次到达原点O之前,若点P、点Q到数轴原点的距离恰好相等,求t的值;
②我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,请求出此时点C对应的数.
![]()
已知点O为数轴的原点,点A表示的数为 , 点B表示的数为4,点C表示的数为x,若点A与点C关于线段
“中线对称”,则x的最大值为.
①的最小值为 ▲ ;
②的值为 ▲ .
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列−1,2,3的最佳值为;数列3,−1,2的最佳值为1;…,经过研究,东东发现,对于“2,−1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
. 根据以上材料,回答下列问题:

数字 形式 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
纵式 |
|
|
|
| |||||
横式 |
|
|
|
|
|
|
|
|
|
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如“![]()
![]()
![]()
![]() ”表示的数是6728,“
”表示的数是6728,“![]()
![]()
![]() ”表示的数是6708,若已知一个用这种方式表示的四位数中含有“
”表示的数是6708,若已知一个用这种方式表示的四位数中含有“”、“
![]() ”和两个空位,则这个四位数是.
”和两个空位,则这个四位数是.
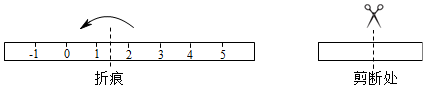
![]()
![]()
回答下列问题:
①则与表示10的点重合的点表示的数是 ▲ .
②这时如果 ,
在
的左侧
两点之间的距离为2022,且
,
两点经过折叠后重合,则
,
表示的数分别是多少?

【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
①A、B两点间的距离AB=,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .





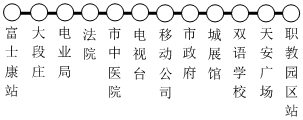
某天,小王从电业局站出发,始终在该线路的公交站点做志愿者服务,到站下车时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下
单位:站
:+5,-2,+6,-11,+8﹐+1,-3,-2,-4,+7