

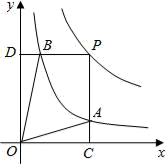


①k的值为;
②点D的坐标为;


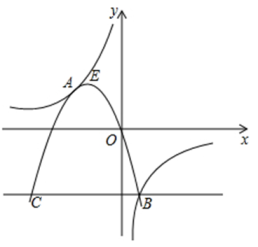

求证:直线
与直线
为“等腰三角线”;
过点
作
轴的垂线
, 在直线
上存在一点
;连接
, 当
时,求出线段
的值
用含
的代数式表示
.
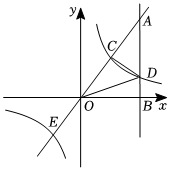

①直接写出的最小值: .
②的面积是否发生变化,如果变化,请说明理由;如果不变化,请求出
的面积.

如图1,在平面直角坐标系中,菱形的顶点
在
轴上,反比例函数
(
)的图象经过点
, 并与线段
交于点
, 反比例函数
(
)的图象经过点
,
交
轴于点
. 已知
.
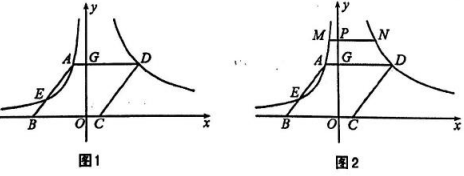
①当时,求
的值;
②在点运动过程中,是否存在某一时刻,使
?若存在,直接写出点
的坐标;若不存在,说明理由.