备考2024年中考数学核心素养专题二十二圆的综合问题

更新时间：2024-03-31 浏览次数：54 类型：二轮复习

一、选择题

1. (2023九上·昆明月考) 在等腰直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， D是 $\text{[math]}$ 边上一动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为直径的圆交 $\text{[math]}$ 于点E ，则 $\text{[math]}$ 长的最小值是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
2. (2023·合肥模拟) 如图，点P是 $\text{[math]}$ 外的一点，PA、PC是 $\text{[math]}$ 的切线，切点分别为A，C，AB是 $\text{[math]}$ 的直径，连接BC，PO，PO交弦AC于点D．下列结论中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 若 $\text{[math]}$ ，则△PAC是等边三角形 D . 若△PAC是等边三角形，则 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九上·通州月考) 如图，AB是半圆O的直径，按以下步骤作图：
（1）分别以A，B为圆心，大于AO长为半径作弧，两弧交于点P，连接OP与半圆交于点C；（2）分别以A，C为圆心，大于 $\text{[math]}$ AC长为半径作弧，两弧交于点Q，连接OQ与半圆交于点D；（3）连接AD，BD，BC，BD与OC交于点 E．根据以上作图过程及所作图形，下列结论：①BD平分∠ABC；②BC∥OD；③CE＝OE；④AD²＝OD•CE；所有正确结论的序号是（）

A . ①② B . ①④ C . ②③ D . ①②④

答案解析收藏纠错 + 选题
4. (2022·兰陵模拟) 如图，在⊙O中，AB是⊙O的直径，AB＝10， $\text{[math]}$ ，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE=30°；②∠DOB=2∠CED；③DM⊥CE；④CM+DM的最小值是10，上述结论中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2023九上·期末) 如图，在 $\text{[math]}$ 中，弦BC，ED所对的圆心角分别是 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 互补，已知 $\text{[math]}$ .当 $\text{[math]}$ 时，弦BC与DE之间的距离等于（）.

A . 7 B . 1或7 C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·德阳) 如图， $\text{[math]}$ 的直径 $\text{[math]}$ ， $\text{[math]}$ 是弦， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ ， $\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．下列结论中正确的个数是（）
① $\text{[math]}$ ；

② $\text{[math]}$ 是 $\text{[math]}$ 的切线；

③B，E两点间的距离是 $\text{[math]}$ ；

④ $\text{[math]}$ ．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2023·南山模拟) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 经过点C，连接 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ .连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则以下结论：① $\text{[math]}$ ；② $\text{[math]}$ 为 $\text{[math]}$ 的切线；③ $\text{[math]}$ ；④ $\text{[math]}$ ；则正确的结论个数为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2023·梅州模拟) 如题图所示，已知一个半径为2的 $\text{[math]}$ ， P为平面内一个点，过点P作 $\text{[math]}$ 的两条切线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的一条直径，且 $\text{[math]}$ ，连接若干条线段的端点．若 $\text{[math]}$ ，下列给出的四个命题中，为假命题的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 为正三角形 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·庆云期中) 如图，点A、B分别在x轴、y轴上（ $\text{[math]}$ ）；以 $\text{[math]}$ 为直径的圆经过原点O，C是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积等于5；④若 $\text{[math]}$ ，则点C的坐标是 $\text{[math]}$ ，其中正确的结论有（　　）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
10. (2021九上·莘县期中) 如图，点E是 $\text{[math]}$ 的内心，连接AE并延长交BC于点F，交 $\text{[math]}$ 的外接圆于点D，连接BD．以下结论：①AE平分 $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ，其中正确的结论有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题

二、填空题

11. (2023·和平模拟) 如图，圆内接四边形 $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
12. 如图，在Rt△ABC中，∠C=90°，E为AB边上一点.以AE为直径的圆О与BC相切于点D，连结AD，BE= $\text{[math]}$ ， BD=3.5.P是AB边上的动点，当△ADP为等腰三角形时，AP的长为.

答案解析收藏纠错 + 选题
13. (2023·临潼模拟) 如图所示， $\text{[math]}$ 为矩形 $\text{[math]}$ 中 $\text{[math]}$ 边上的一点，已知 $\text{[math]}$ ， $\text{[math]}$ ，若点 $\text{[math]}$ 在矩形 $\text{[math]}$ 内部，且 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
14. (2023·泰州模拟) $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， E是AC的中点，MN分别是边AB、BC上的动点，D也是BC边上的一个动点，以CD为直径作 $\text{[math]}$ ，连接ED交 $\text{[math]}$ 于F，连接FM，MN，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题
15. (2022九上·海淀期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是某圆内接正六边形、正方形、等边三角形的一边．若 $\text{[math]}$ ，下面四个结论中，
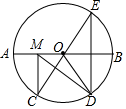
①该圆的半径为2； ② $\text{[math]}$ 的长为 $\text{[math]}$ ；
③ $\text{[math]}$ 平分 $\text{[math]}$ ； ④连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的面积比为 $\text{[math]}$ ．
所有正确结论的序号是．

答案解析收藏纠错 + 选题

三、解答题

16. (2024九上·杭州月考) 如图，在锐角 $\text{[math]}$ 中， $\text{[math]}$ 是最短边．以 $\text{[math]}$ 为直径的 $\text{[math]}$ ，交 $\text{[math]}$ 于D ，过O作 $\text{[math]}$ ，交 $\text{[math]}$ 于E ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
17. (2023九上·长沙月考) 如图：四边形 $\text{[math]}$ 内接于圆 $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．
1. （1）判断 $\text{[math]}$ 与圆 $\text{[math]}$ 的位置关系，并说明理由；
2. （2）若 $\text{[math]}$ ，求证： $\text{[math]}$ 为弧 $\text{[math]}$ 的中点；
3. （3）在（2）的条件下，若 $\text{[math]}$ ， $\text{[math]}$ ，求劣弧 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
18. (2024·湖南模拟) 已知四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，直径 $\text{[math]}$ 于点F ．
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）如图2，连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ，过点D作 $\text{[math]}$ 于点H ，求证： $\text{[math]}$ ；
3. （3）如图3，在（2）的条件下，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
19. 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，以AB为直径的 $\text{[math]}$ 与AC交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是BC的中点，连结BD，DE
1. （1）求证：DE是 $\text{[math]}$ 的切线.
2. （2）若 $\text{[math]}$ ，求AD的长
3. （3）在（2）的条件下，点P是 $\text{[math]}$ 上一动点，求PA＋PB的最大值.
答案解析收藏纠错 + 选题
20. (2024九上·湖南期末) 如图1，⊙O的直径CD垂直弦AB于点E ，且CE＝8，DE＝2．
1. （1）求AB的长．
2. （2）探究拓展：如图2，连接AC ，点G是 $\text{[math]}$ 上一动点，连接AG ，延长CG交AB的延长线于点F ．
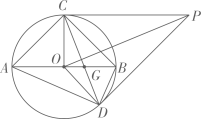
  ①当点G是 $\text{[math]}$ 的中点时，求证：∠GAF＝∠F；
  ②如图3，连接DF ， BG ，当△CDF为等腰三角形时，请计算BG的长．
答案解析收藏纠错 + 选题
21. 如图，△ABD内接于半径为5的⊙O，连结AO并延长交BD于点M，交⊙O于点C，过点A作AE// BD，交CD的延长线于点E，AB=AM.
1. （1）求证：△ABM∽△ECA.
2. （2）当CM=4OM时，求AD的长.
3. （3）当CM= kOM时，设△MCD的面积为S₁ ， △ADE的面积为S₂ ，求 $\text{[math]}$ 的值（用含k的代数式表示）.
答案解析收藏纠错 + 选题
22. (2024九上·潮南期末) 圆内接四边形若有一组邻边相等，则称之为等邻边圆内接四边形.
1. （1）如图1，四边形 $\text{[math]}$ 为等邻边圆内接四边形， $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ 的度数；
2. （2）如图2，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ ， $\text{[math]}$ ，若四边形 $\text{[math]}$ 为等邻边圆内接四边形， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
3. （3）如图3，四边形 $\text{[math]}$ 为等邻边圆内接四边形， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的直径，且 $\text{[math]}$ .设 $\text{[math]}$ ，四边形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，试确定 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式，并求出 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
23. (2023九上·北京市期中) 在平面直角坐标系 $\text{[math]}$ 中，已知圆 $\text{[math]}$ 和图形 $\text{[math]}$ ，将图形 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称得到图形 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上任意一点， $\text{[math]}$ 为圆 $\text{[math]}$ 上任意一点，将 $\text{[math]}$ 的最大值称为图形 $\text{[math]}$ 关于 $\text{[math]}$ 的“对称长度”．
1. （1）若圆 $\text{[math]}$ 半径为 $\text{[math]}$ ；
  ①在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个点中，关于直线 $\text{[math]}$ 的“对称长度”为 $\text{[math]}$ ；
  ②已知直线 $\text{[math]}$ ： $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则在线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，关于 $\text{[math]}$ 的“对称长度”为 $\text{[math]}$ 的是；
2. （2）圆 $\text{[math]}$ 半径为 $\text{[math]}$ ，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧，直线 $\text{[math]}$ 从 $\text{[math]}$ 开始，绕点 $\text{[math]}$ 顺时针旋转到 $\text{[math]}$ ，在 $\text{[math]}$ 旋转过程中，求正方形 $\text{[math]}$ 关于 $\text{[math]}$ 的“对称长度” $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
24. (2023九上·温州月考) 如图1， $\text{[math]}$ 内接于圆 $\text{[math]}$ 为直径，点 $\text{[math]}$ 在 $\text{[math]}$ 的上方，且 $\text{[math]}$ ．连结 $\text{[math]}$ 是 $\text{[math]}$ 边上的高，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
3. （3）如图2，取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连结 $\text{[math]}$ ．
  ①若 $\text{[math]}$ ，在点 $\text{[math]}$ 运动的过程中，当四边形 $\text{[math]}$ 的其中一边长是 $\text{[math]}$ 的2倍时，求所有满足条件的 $\text{[math]}$ 的长．
  ②连结 $\text{[math]}$ ，当 $\text{[math]}$ 的面积是 $\text{[math]}$ 的面积的2倍时，则 $\text{[math]}$ ▲ （请直接写出答案）
答案解析收藏纠错 + 选题

四、综合题

25. (2024九上·温岭期末) 如图⊙O半径为r，锐角△ABC内接于⊙O，连AO并延长交BC于D，过点D作DE⊥AC于E．
1. （1）如图1，求证：∠DAB＝∠CDE；
2. （2）如图1，若CD＝OA，AB＝6，求DE的长；
3. （3）如图2，当∠DAC＝2∠DAB时，BD＝5，DC＝6，求r的值；
4. （4）如图3，若AE＝AB＝BD＝1，直接写出AD＋DE的值（用含r的代数式表示）
答案解析收藏纠错 + 选题
26. (2024九上·巴彦期末) 如图1， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为直径，点D为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G， $\text{[math]}$ 于点F交 $\text{[math]}$ 于点E．
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）在（2）的条件下，如图3，点H是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
27. (2024九上·哈尔滨期末) 在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 与直径 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$
1. （1）如图，求证： $\text{[math]}$ ．
2. （2）如图，点 $\text{[math]}$ 在 $\text{[math]}$ 延长线上， $\text{[math]}$ 切 $\text{[math]}$ 于点 $\text{[math]}$ 交 $\text{[math]}$ 延长线于 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，求证： $\text{[math]}$ ．
3. （3）如图，在 $\text{[math]}$ 的条件下，连接 $\text{[math]}$ 和 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
28. (2023九上·长沙月考) 已知在以点 $\text{[math]}$ 为原点、 $\text{[math]}$ 所在直线为 $\text{[math]}$ 轴的平面直角坐标系中，圆内接四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 经过 $\text{[math]}$ 的内心，且抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点．
1. （1）求证： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3） $\text{[math]}$ 、 $\text{[math]}$ 、四边形 $\text{[math]}$ 的面积分别记为 $\text{[math]}$ ， $\text{[math]}$ 、S ，求同时满足以下三个条件的抛物线的解析式；
  ① $\text{[math]}$ ，
  ② $\text{[math]}$ ，
  ③四边形 $\text{[math]}$ 的周长为 $\text{[math]}$ .
答案解析收藏纠错 + 选题

五、实践探究题

29. (2022·吉林月考)
1. （1）【感知】如图（1）已知四边形 $\text{[math]}$ 是圆O的内接四边形， $\text{[math]}$ ，易知 $\text{[math]}$ ．（不用证明）
2. （2）【拓展】在【感知】的条件下， $\text{[math]}$ 与 $\text{[math]}$ 交于点E，已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
3. （3）【应用】已知 $\text{[math]}$ 中 $\text{[math]}$ ，点D为 $\text{[math]}$ 中点，以 $\text{[math]}$ 为斜边向上作等腰直角三角形，当 $\text{[math]}$ 把 $\text{[math]}$ 的面积分为 $\text{[math]}$ 两部分时， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
30. (2023九上·温岭期中) 如图1，扇形AOB中，∠AOB＝90°，OA＝6，点P在半径OB上，连接AP ．
1. （1）把△AOP沿AP翻折，点O的对称点为点Q ．
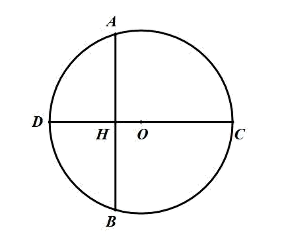
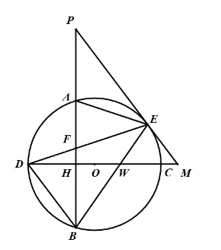
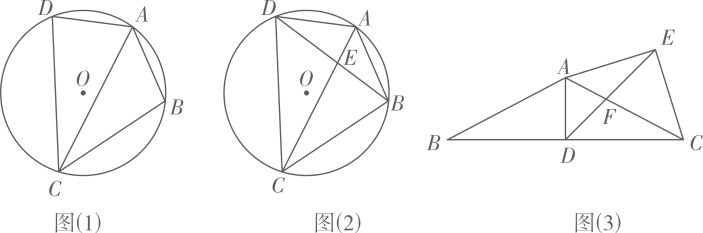
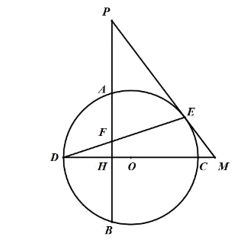
  ①当点Q刚好落在弧AB上，求弧AQ的长；
  ②如图2，点Q落在扇形AOB外，AQ与弧AB交于点C ，过点Q作QH⊥OA ，垂足为H ，
  探究OH、AH、QC之间的数量关系，并说明理由；
2. （2）如图3，记扇形AOB在直线AP上方的部分为图形W ，把图形W沿着AP翻折，点B的对称点为点E ，弧AE与OA交于点F ，若OF＝2，求PO的长．
答案解析收藏纠错 + 选题