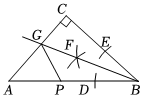
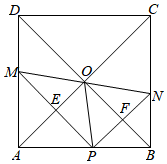
(1);(2)PE=2BF;(3)在点P运动的过程中,当GB=GP时,
;(4)当P为BC的中点时,
.
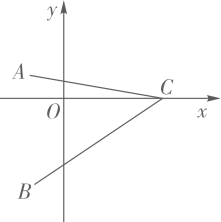
若
,
, 求
的值;
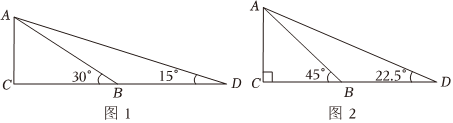
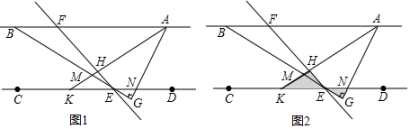
已知:如图1,是
的个外角.
求证:.

如图1,若与
互为“顶补等腰三角形”.
,
于
,
于
, 求证:
;
如图2,在四边形中,
,
,
,
, 在四边形
的内部是否存在点
, 使得
与
互为“顶补等腰三角形”?若存在,请给予证明;若不存在,请说明理由.
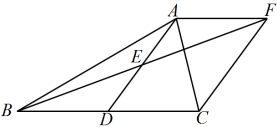
②除了①中两种情况以外,还有其他情况吗?如果有,请直接写出这三个角的数量关系.