2024年中考数学热点探究二十三设计方案

更新时间：2024-04-28 浏览次数：71 类型：二轮复习

一、选择题

1. (2023九上·菏泽月考) 在数学活动课上，老师让同学们判断一个由四根木条组成的四边形是否为矩形，下面是一个学习小组拟定的方案，其中正确的方案是（）

A . 测量四边形的三个角是否为直角 B . 测量四边形的两组对边是否相等
C . 测量四边形的对角线是否互相平分 D . 测量四边形的其中一组邻边是否相等

答案解析收藏纠错 + 选题
2. (2023九上·安徽期中) 某班计划在劳动实践基地内种植蔬菜，班长买回来10米长的围栏，准备围成两边靠墙（两墙垂直且足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰直角三角形（两直角边靠墙）、扇形这三种方案，如图所示．最佳方案是（）

A . 方案1 B . 方案2 C . 方案1或方案2 D . 方案3

答案解析收藏纠错 + 选题
3. 九年级2班计划在劳动实践基地内种植蔬菜，班长买回来8米长的围栏，准备围成一边靠墙（墙足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形，等腰三角形（底边靠墙），半圆形这三种方案，最佳方案是（）

A . 方案1 B . 方案2 C . 方案3 D . 方案1或方案2

答案解析收藏纠错 + 选题
4. (2023七下·济南高新技术产业开发期末) 要得知某一池塘两端A，B的距离，发现其无法直接测量，两同学提供了如下间接测量方案．
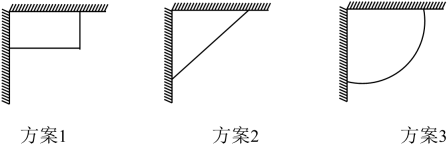
方案Ⅰ：如图1，先过点B作 $\text{[math]}$ ，再在 $\text{[math]}$ 上取C，D两点，使 $\text{[math]}$ ，接着过点D作 $\text{[math]}$ 的垂线 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点E，则测量 $\text{[math]}$ 的长即可；
方案Ⅱ：如图2，过点B作 $\text{[math]}$ ，再由点D观测，用测角仪在 $\text{[math]}$ 的延长线上取一点C，使 $\text{[math]}$ ，则测量 $\text{[math]}$ 的长即可．
对于方案Ⅰ、Ⅱ，说法正确的是（）

A . 只有方案Ⅰ可行 B . 只有方案Ⅱ可行 C . 方案Ⅰ和Ⅱ都可行 D . 方案Ⅰ和Ⅱ都不可行

答案解析收藏纠错 + 选题
5. (2023·北京市模拟) 某产品的盈利额（即产品的销售价格与固定成本之差）记为y，购买人数记为x，其函数图象如图1所示．由于日前该产品盈利未达到预期，相关人员提出了两种调整方案，图2，图3中的实线分别为调整后y与x的函数图象．给出下列四种说法，其中正确说法的序号是（　　）
①图2对应的方案是：保持销售价格不变，并降低成本；

②图2对应的方案是：提高销售价格，并提高成本；

③图3对应的方案是：提高销售价格，并降低成本

④图3对应的方案是：提高销售价格，并保持成本不变

A . ①③ B . ②③ C . ①④ D . ②④

答案解析收藏纠错 + 选题

二、填空题

6. (2022·瓯海模拟) 小芳和小林为了研究图中“跑到画板外面去的两直线a，b所成的角（锐角）”问题，设计出如下两个方案：
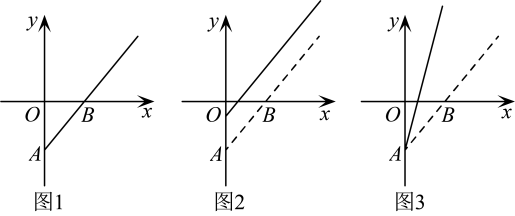
小林的方案
小芳的方案
测α，β的度数．
测∠1，∠ACB的度数．
已知小林测得∠β＝115°，小芳作了AB＝BC，并测得∠1＝80°，则直线a，b所成的角为．

答案解析收藏纠错 + 选题
7. (2024七下·思明期末) 生物工作者为了估计一片山林中雀鸟的数量，设计了如下方案：先捕捉50只雀鸟，给它们做上标记后放回山林；一段时间后，再从山林中随机捕捉80只，其中有标记的雀鸟有2只，请你帮助工作人员估计这片山林中雀鸟的数量为只．

答案解析收藏纠错 + 选题
8. (2022·平邑模拟) 数学课上，李老师提出如下问题：
已知：如图， $\text{[math]}$ 是⊙O的直径，射线 $\text{[math]}$ 交⊙O于 $\text{[math]}$ ．

求作：弧 $\text{[math]}$ 的中点D ．

同学们分享了如下四种方案：

①如图1，连接BC ，作BC的垂直平分线，交⊙O于点D ．

②如图2，过点O作AC的平行线，交⊙O于点D ．

③如图3，作∠BAC的平分线，交⊙O于点D ．

④如图4，在射线AC上截取AE ，使AE=AB ，连接BE ，交⊙O于点D ．

上述四种方案中，正确的方案的序号是．

答案解析收藏纠错 + 选题
9. (2022·房山模拟) 为确定传染病的感染者，医学上可采用“二分检测方案”．假设待检测的总人数是 $\text{[math]}$ （ $\text{[math]}$ 为正整数）．将这 $\text{[math]}$ 个人的样本混合在一起做第1轮检测（检测1次），如果检测结果是阴性，可确定这些人都未感染；如果检测结果是阳性，可确实其中感染者，则将这些人平均分成两组，每组 $\text{[math]}$ 个人的样本混合在一起做第2轮检测，每组检测1次．依此类推：每轮检测后，排除结果为阴性的组，而将每个结果为阳性的组再平均分成两组，做下轮检测，直至确定所有的感染者．
例如，当待检测的总人数为8，且标记为“ $\text{[math]}$ ”的人是唯一感染者时，“二分检测方案”可用如图所示．从图中可以看出，需要经过4轮共 $\text{[math]}$ 次检测后，才能确定标记为“ $\text{[math]}$ ”的人是唯一感染者．
1. （1） n的值为；
2. （2）若待检测的总人数为8，采用“二分检测方案”，经过4轮共9次检测后确定了所有的感染者，写出感染者人数的所有可能值；
答案解析收藏纠错 + 选题

三、实践探究题

10. (2024·镇海区月考) 根据以下素材，探索完成任务．

如何确定木板分配方案？
素材1	我校开展爱心义卖活动，小艺和同学们打算推销自己的手工制品．他们以每块15元的价格买了100张长方形木板，每块木板长和宽分别为80cm，40cm.
素材2	现将部分木板按图1虚线裁剪，剪去四个边长相同的小正方形（阴影）．把剩余五个矩形拼制成无盖长方体收纳盒，使其底面长与宽之比为3：1．其余木板按图2虚线裁剪出两块木板（阴影是余料），给部分盒子配上盖子．
素材3	义卖时的售价如标签所示：
问题解决
任务1	计算盒子高度	求出长方体收纳盒的高度．
任务2	确定分配方案1	若制成的有盖收纳盒个数大于无盖收纳盒，但不到无盖收纳盒个数的2倍，木板该如何分配？请给出分配方案．
任务3	确定分配方案2	为了提高利润，小艺打算把图2裁剪下来的余料（阴影部分）利用起来，一张矩形余料可以制成一把小木剑，并以5元/个的价格销售．请确定木板分配方案，使销售后获得最大利润．

答案解析收藏纠错 + 选题

11. (2023九上·温州月考) 某校准备在校园里利用围墙（墙可用最大长度为 $\text{[math]}$ ）和 $\text{[math]}$ 长的篱笆墙，围成Ⅰ、Ⅱ两块矩形开心农场．某数学兴趣小组设计了三种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：
1. （1）方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度 $\text{[math]}$ 的矩形水池，且需保证总种植面积为 $\text{[math]}$ ，试确定 $\text{[math]}$ 的长；
2. （2）方案二：如图②，使围成的两块矩形总种植面积最大，请问 $\text{[math]}$ 应设计为多长？此时最大面积为多少？
3. （3）方案三：如图③，在图中所示三处位置各留 $\text{[math]}$ 宽的门，且使围成的两块矩形总种植面积最大，请问 $\text{[math]}$ 应设计为多长？此时最大面积为多少？
答案解析收藏纠错 + 选题
12. 【综合与实践】
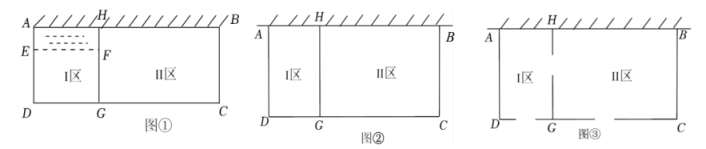
有言道：“杆秤一头称起人间生计，一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤.小组先设计方案，然后动手制作，再结合实际进行调试，请完成下列方案设计中的任务.
【知识背景】如图，称重物时，移动秤砣可使杆秤平衡，根据杠杆原理推导得： $\text{[math]}$ $\text{[math]}$ .其中秤盘质量 $\text{[math]}$ 克，重物质量 $\text{[math]}$ 克，秤砣质量 $\text{[math]}$ 克，秤纽与秤盘的水平距离为 $\text{[math]}$ 厘米，科纽与零刻线的水平距离为 $\text{[math]}$ 厘米，秤砣与零刻线的水平距离为 $\text{[math]}$ 厘米.
【方案设计】
目标：设计简易杆秤.设定 $\text{[math]}$ ，最大可称重物质量为1000克，零刻线与末刻线的距离定为50厘米.
1. （1）当秤盘不放重物，秤砣在零刻线时，杆秤平衡，请列出关于l，a的方程；
2. （2）当秤盘放入质量为1000克的重物，秤砣从零刻度线移至末刻线时，杠杆平衡，请列出关于l，a的方程；
3. （3）根据(1)和(2)所列方程，求出l和 $\text{[math]}$ 的值；
4. （4）根据（1）-（3），求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；
5. （5）从零刻线开始，每隔100克在科杆上找到对应刻线，请写出相邻刻线间的距离.
答案解析收藏纠错 + 选题

13. (2023九上·长清期中) 某校项目式学习小组开展项目活动，过程如下：

项目主题：测量旗杆高度

问题驱动：能利用哪些科学原理来测量旗杆的高度？

组内探究：由于旗杆较高，需要借助一些工具来测量，比如自制的直角三角形硬纸板，标杆，镜子，甚至还可以利用无人机…确定方法后，先画出测量示意图，然后实地进行测量，并得到具体数据，从而计算旗杆的高度．

成果展示：下面是同学们进行交流展示时的部分测量方案：

	方案一		方案二		…
测量工具	标杆，皮尺		自制直角三角板硬纸板，皮尺		…
测量示意图	说明：线段AB表示学校旗杆，小明的眼睛到地面的距离CD＝1.7m，测点F与B，D在同一水平直线上，D，F，B之间的距离都可以直接测得，且A，B，C，D，E，F都在同一竖直平面内，点A，C，E三点在同一直线上．		说明：线段AB表示旗杆，小明的身高CD＝1.7m，测点D与B在同一水平直线上，D，B之间的距离可以直接测得，且A，B，C，D，E，F，G都在同一竖直平面内，点A，C，E三点在同一直线上，点C，F，G三点在同一直线上．
测量数据	B，D之间的距离	16.8m	B，D之间的距离	16.8m	…
	D，F之间的距离	1.35m	EF的长度	0.50m	…
	EF的长度	2.60m	CE的长度	0.75m	…
…	…

根据上述方案及数据，请你选择一个方案，求出学校旗杆AB的高度．（结果精确到0.1m）；

答案解析收藏纠错 + 选题

14. (2024九上·杭州月考) 根据以下素材，探索完成任务．

如何设计喷泉喷头的升降方案？

素材1

如图，有一个可垂直升降的喷泉，喷出的水柱呈抛物线．记水柱上某一点到喷头的水平距离为x米，到湖面的垂直高度为y米．当喷头位于起始位置时，测量得x与y的四组数据如下：

x（米）	0	2	3	4
y（米）	1	2	1.75	1

素材2

公园想设立新的游玩项目，通过升降喷头，使游船能从水柱下方通过，如图，为避免游船被喷泉淋到，要求游船从水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.4米．已知游船顶棚宽度为2.8米，顶棚到湖面的高度为2米．

问题解决

任务1

确定喷泉形状

结合素材1，求y关于x的表达式．

任务2

探究喷头升降方案

为使游船按素材2要求顺利通过，求喷头距离湖面高度的最小值．

答案解析收藏纠错 + 选题

15. (2023九上·兰溪月考) 根据素材解决问题．

设计货船通过圆形拱桥的方案
素材1	图1中有一座圆拱石桥，图2是其圆形桥拱的示意图，测得水面宽AB=16m，拱顶离水面的距离CD=4m．
素材2	如图3，一艘货船露出水面部分的横截面为矩形EFGH，测得EF=3m，EH=10m．因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度y(米)与货船增加的载重量x (吨)满足函数关系式y= $\text{[math]}$ x．
问题解决
任务1	确定桥拱半径	求圆形桥拱的半径．
任务2	拟定设计方案	根据图3状态，货船能否通过圆形桥拱？若能，最多还能卸载多少吨货物？若不能，至少要增加多少吨货物才能通过？

答案解析收藏纠错 + 选题

16. (2024九下·宁波月考) 根据以下素材，探索完成任务．

如何确定拍照打卡板
素材一	设计师小聪为某商场设计拍照打卡板（如图1），图2为其平面设计图．该打卡板是轴对称图形，由长方形DEFG和等腰三角形ABC组成，且点B ， F ， G ， C四点共线．其中，点A到BC的距离为1.2米， $\text{[math]}$ 米， $\text{[math]}$ 米．
素材二	因考虑牢固耐用，小聪打算选用甲、乙两种材料分别制作长方形DEFG与等腰三角形ABC（两种图形无缝隙拼接），且甲材料的单价为85元/平方米，乙材料的单价为100元/平方米．
问题解决
任务一	推理最大高度	小聪说：“如果我设计的方案中CB长与C ， D两点间的距离相等，那么最高点B到地面的距离就是线段DG长”，他的说法对吗？请判断并说明理由．
任务二	探究等腰三角形ABC面积	假设CG长度为x米，等腰三角形ABC的面积为S ，求S关于x的函数表达式．
任务三	确定拍照打卡板	小聪发现他设计的方案中，制作拍照打卡板的总费用不超过180元，请你确定CG长度的最大值．

答案解析收藏纠错 + 选题

17. (2024九上·杭州月考) 根据以下素材，探索完成任务

如何设计拱桥上救生圈的悬挂方案?
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示．某时测得水面宽 $\text{[math]}$ ，拱顶离水面最大距离为10m，抛物线拱形最高点与x轴的距离为5m．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，救生圈悬挂点为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m．为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）

任务1	确定桥拱形状	根据图2，求抛物线的函数表达式．
任务2	拟定设计方案	求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
任务3	探究救生绳长度	当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）

问题解决

（1）任务1 确定桥拱形状
根据图2，求抛物线的函数表达式．
（2）任务2 拟定设计方案
求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
（3）任务3 探究救生绳长度
当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）

答案解析收藏纠错 + 选题

18. (2023九上·浙江期中) 根据以下素材，探索完成任务．

绿化带灌溉车的操作方案

素材1	辆绿化带灌溉车正在作业，水从喷水口喷出，水流的上下两边缘可以抽象为两条抛物线的一部分：喷水口离开地面高1.6米，上边缘抛物线最高点离喷水口的水平距离为3米，高出\|喷水口0.9米，下边缘水流形状与上边缘相同，且喷水口是最高点。
素材2	路边的绿化带宽4米
素材3	绿化带正中间种植了行道树，为了防治病虫害、增加行道树的成活率，园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。

问题解决

（1）任务1：确定上边缘水流形状
建立如图所示直角坐标系，求上边缘抛物线的函数表达式．
（2）任务2：探究灌溉范围
灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗？请说明理由．
（3）任务3：拟定设计方案
灌溉时，发现水流的上下两边缘冲击力最强，喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响，并说明理由；若你认为有影响，请给出具体的“打针”范围。

答案解析收藏纠错 + 选题

19. (2023九上·拱墅月考) 根据以下素材，探索完成任务．

如何设计拱桥上救生圈的悬挂方案？
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，过抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，某时测得水面宽20m ，拱顶离水面最大距离为10m ，抛物线拱形最高点与x轴的距离为5m ．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m.为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）

问题解决：

（1）任务1：确定桥拱形状
根据图2，求抛物线的函数表达式．
（2）任务2：拟定设计方案
求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
（3）任务3：探究救生绳长度
当水位达到最高时，上游一个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数．）

答案解析收藏纠错 + 选题

20. (2023九上·龙湾期中) 根据素材回答问题：

素材1	如图1，空地上有两条互相垂直的小路OP，OQ，中间有一正方形ABCD水池，已知水池的边长为4 米，AB//OQ，AD//OP，且AB与OQ的距离为10 米，AD与OP的距离为8 米．
素材2	现利用两条小路，再购置30 米长的栅栏(图中的细实线）在空地上围出一个花圃，要求围起来的栅栏与小路相互平行（或垂直），靠小路和水池的都不需要栅栏，接口损耗忽略不计．
	任务1	任务2
	小明同学按如图2的设计，若EF=16米，求出花圃的面积（不包含水池的面积）．	若按如图3、如图4设计方案，通过计算说明哪种方案的最大面积更大．
项目反思	如果栅栏不一定与墙面垂直（或平行），你还能设计出比以上方案面积更大的花圃吗？某学习小组在探究的过程中，设计了方案如图5，你认为图5的最大面积与以上方案比较，哪个更大，请通过计算说明．

答案解析收藏纠错 + 选题

21. 根据以下素材，探索完成任务.如何设计拱桥景观灯的悬挂方案？
素材1
图1中有一座拱桥，图2是某抛物线形桥拱的示意图，某时测得水面宽20m，拱顶离水面5m.据调查，该河段水位在此基础上再涨1.8m达到最高.
素材2
为迎佳节，拟在图1桥沿前面的桥拱上悬挂40cm长的灯笼，如图3.为了安全，灯笼底部距离水面不小于1m；为了实效，相邻两盏灯笼悬挂点的水平间距均为1.6m；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布.

问题解决
1. （1）任务1
  确定桥拱形状
  在图2中建立合适的直角坐标系，求抛物线的函数表达式.
2. （2）任务2
  探究悬挂范围
  在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围.
3. （3）任务3
  拟定设计方案
  给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标.
答案解析收藏纠错 + 选题

22. (2023九上·上虞月考) 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽40m，拱顶离水面8m．据调查，该河段水位在此基础上再涨2.1m达到最高．
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼，如图3．为了安全，灯笼底部距离水面不小于1m；为了实效，相邻两盏灯笼悬挂点的水平间距均为1.6m；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．

问题解决

（1）任务1：确定桥拱形状：
在图2建立合适的直角坐标系，求抛物线的函数表达式．
（2）任务2：探究悬挂范围：
在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
（3）任务3：拟定设计方案：
给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

答案解析收藏纠错 + 选题

23. (2023九上·龙湾开学考) 根据以下信息，探索完成任务．
如何设计种植方案？
素材1：
某校为响应国家政策，在校内 $\text{[math]}$ 平方米的土地上进行种植课实践，现有 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 三种作物的相关信息如表所示 $\text{[math]}$ 已知 $\text{[math]}$ 株 $\text{[math]}$ 作物和 $\text{[math]}$ 株 $\text{[math]}$ 作物的产量共为 $\text{[math]}$ 千克： $\text{[math]}$ 株 $\text{[math]}$ 作物和 $\text{[math]}$ 株 $\text{[math]}$ 作物的产量共为 $\text{[math]}$ 千克．

$\text{[math]}$ 作物
$\text{[math]}$ 作物
$\text{[math]}$ 作物
每平方米种植株树 $\text{[math]}$ 株 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
单株产量 $\text{[math]}$ 千克 $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
素材2：
由于 $\text{[math]}$ 作物植株间距较大，可增加 $\text{[math]}$ 作物每平方米的种植株树 $\text{[math]}$ 经过实验发现，每平方米种植 $\text{[math]}$ 作物每增加 $\text{[math]}$ 株， $\text{[math]}$ 作物的单株产量减少 $\text{[math]}$ 千克 $\text{[math]}$ 而 $\text{[math]}$ ， $\text{[math]}$ 单株产量不发生变化．
素材3：
若同时种植 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种作物，实行分区域种植．
问题解决：
1. （1）任务1：确定单株产量
  求 $\text{[math]}$ ， $\text{[math]}$ 的值．
2. （2）任务2：单一种植 $\text{[math]}$ 全部种植 $\text{[math]}$ 作物 $\text{[math]}$ ，预估种植策略
  要使 $\text{[math]}$ 作物每平方米产量为 $\text{[math]}$ 千克，则每平方米应种植多少株？
3. （3）任务3：分区种植 $\text{[math]}$ 种植 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种作物 $\text{[math]}$ ，规划种植方案
  设这 $\text{[math]}$ 平方米的土地中有 $\text{[math]}$ 平方米用于种植 $\text{[math]}$ 作物，且每平方米的产量最大：有 $\text{[math]}$ 平方米用于种植 $\text{[math]}$ 作物，剩余的全用来种植 $\text{[math]}$ 作物， $\text{[math]}$ ， $\text{[math]}$ 均为正整数 $\text{[math]}$ 当这 $\text{[math]}$ 平方米总产量为 $\text{[math]}$ 千克时，求这三种作物的种植方案．
答案解析收藏纠错 + 选题

24. (2024·瑞昌模拟) 根据以下材料，探索完成任务：

智能浇灌系统使用方案
材料			如图1是一款智能浇灌系统，水管OP垂直于地面并可以随意调节高度（OP最大高度不超过2.4m），浇灌花木时，喷头P处会向四周喷射水流形成固定形状的抛物线，水流落地点M与点O的距离即为最大浇灌距离，各方向水流落地点形成一个以点O为圆心，OM为半径的圆形浇灌区域．当喷头P位于地面与点O重合时，某一方向的水流上边缘形成了如图2的抛物线，经测量， $\text{[math]}$ ，水流最高时距离地面0.1m．如图3，农科院将该智能浇灌系统应用于一个长8m，宽6m的矩形试验田中，水管放置在矩形中心O处．
问题解决
任务1	确定水流形状	在图2中建立合适的平面直角坐标系，求抛物线的函数表达式．
任务2	探究浇灌最大区域	当调节水管OP的高度时，浇灌的圆形区域面积会发生变化，请你求出最大浇灌圆形区域面积．（结果保留 $\text{[math]}$ ）
任务3	解决具体问题	若要保证浇灌区域能完全覆盖矩形试验田，则水管OP至少需要调节到什么高度？

答案解析收藏纠错 + 选题

25. (2024九下·温州开学考) 根据下列素材，完成相应任务

仓储品装容的优化设计
素材1	如图1是某个仓库，图2是其横截面的示意图，已知墙体OA=2.6米，BC=5米，水平距离OC=12米，其顶部的轮廓为抛物线的一部分，建立如图所示的平面直角坐标系后它可以近似地用函数 y= $\text{[math]}$ x²+bx+c表示
素材2	图3是棱长为1m的立方体仓储品，将四件一样的仓储品如图4所示叠放在MN处，MN=1m.当叉车要取货物时，需要将其向上抬升10cm，沿水平方向移动1米后取出。
素材3	如图5，为保证能够用叉车安全顺利地搬运和放置仓储品进出仓库，需设计三条宽度为2米的过道OE，HC，FG，以及在过道之间设计两块宽度不少于2米的仓储区域EF，GH. 要求： ①靠近过道的仓储品需从就近过道搬运，其余可从左或右搬运。 ②尽可能多的装容仓储品.
问题解决
任务1	确定顶部形状	求仓库离地的最大距离.
任务2	确定摆放高度	当OM=2.4米时，试分别判断叉车能否从左边或右边取出?请说明理由。
任务3	设计最优方案	已知该仓库的长为50米，请你根据素材和要求设计：仓储区EF= ▲米， GH= ▲米，仓库最大仓储品容量为 ▲件.

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中