浙教版数学八上第2章章末重难点专训等腰三角形和等边三角形

更新时间：2024-08-28 浏览次数：2 类型：复习试卷

一、选择题

1. (2024八下·南海月考) 小明将两把完全相同的长方形直尺如图放置在 $\text{[math]}$ 上，两把直尺的接触点为P ，则射线OP ，即为 $\text{[math]}$ 的角平分线．边OA与其中一把直尺边缘的交点为C ，点C、P在这把直尺上的刻度读数分别是2、5，则OC的长度是（）

A . $\text{[math]}$ B . 2.5 C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
2. (2024八下·南城期中) 如图，在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，下列结论中： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．正确的是（）

A . ①②③ B . ①②④ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题
3. (2024·织金模拟) 点A ， B在直线l同侧，若点C是直线l上的点，且 $\text{[math]}$ 是等腰三角形，则这样的点C最多有（）

A . 5个 B . 4个 C . 3个 D . 2个

答案解析收藏纠错 + 选题
4. (2024八下·顺德期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， BD、CD分别平分 $\text{[math]}$ 、 $\text{[math]}$ ，过点D作直线平行于BC ，交AB、AC于E、F ，则 $\text{[math]}$ 的周长为（）

A . 16 B . 17 C . 18 D . 19

答案解析收藏纠错 + 选题
5. (2024·浙江模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，适当长为半径画弧，交BA于点 $\text{[math]}$ ，交BC于点 $\text{[math]}$ ，分别以点M，N为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 的内部相交于点 $\text{[math]}$ ，画射线BP，交AC于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八上·仙居期末) 如图，在“V”字形图形中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若要求出这个图形的周长，则需添加的一个条件是（）．

A . $\text{[math]}$ 的长 B . $\text{[math]}$ 的长 C . $\text{[math]}$ 的长 D . $\text{[math]}$ 与 $\text{[math]}$ 的和

答案解析收藏纠错 + 选题
7. (2022八上·杭州期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ，过点F作 $\text{[math]}$ 交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点E，那么下列结论：
① $\text{[math]}$ ；② $\text{[math]}$ 为等腰三角形；③ $\text{[math]}$ 的周长等于 $\text{[math]}$ 的周长；④ $\text{[math]}$ .其中正确的是（）

A . ①② B . ①③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
8. (2023八上·新丰期中) 如图，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上一点， $\text{[math]}$ 和 $\text{[math]}$ 是等边三角形．下列结论：
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 是等边三角形；④ $\text{[math]}$ ．其中正确的是（）

A . ① B . ①② C . ①②③ D . ①②③④

答案解析收藏纠错 + 选题
9. (2023八上·洞口期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的平分线， $\text{[math]}$ ，垂足为M，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）．

A . 10 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题
10. (2017七下·东营期末)
如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于D，则DE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·哈尔滨开学考) 如图，P、 $\text{[math]}$ 两点关于 $\text{[math]}$ 对称，P、 $\text{[math]}$ 两点关于 $\text{[math]}$ 对称，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. 如图所示，在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，则图中共有等腰三角形的个数是．

答案解析收藏纠错 + 选题
13. (2024八上·防城期末) 如图，边长为 $\text{[math]}$ 的正三角形 $\text{[math]}$ 向右平移 $\text{[math]}$ ，得到正三角形 $\text{[math]}$ ，此时阴影部分的周长为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2024九下·路桥开学考) 如图，AB＝AC ， D为AC的垂直平分线上一点，且CD=BC，BD＝AB ，则∠A＝．

答案解析收藏纠错 + 选题
15. (2023八上·香坊期中) 如图，在△ABC中，AB＝AC ． E为平面上一点，连接AE、CE ，点D为AE上一点，连接CD、BD ， BD与AC交于点F ，若∠ACB＝∠BDC＝60°，∠E﹣ $\text{[math]}$ ∠CDE＝∠CAD+∠ABD ， BD＝8，AF：AC＝3：8，CE＝ $\text{[math]}$ ． △ABD的面积为．

答案解析收藏纠错 + 选题
16. (2023八上·朝阳期中) 如图，过边长为2的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连接PQ交AC边于D，则下面结论：①PE=2AE；②D为PQ的中点；③CQ=2AE；④CQ+2CD=2；其中正确的结论有：．

答案解析收藏纠错 + 选题

三、解答题

17. (2024八上·赣州期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的高，点E为直线 $\text{[math]}$ 上点，且 $\text{[math]}$ ．
1. （1）如图1，当点E在边 $\text{[math]}$ 上时，求证： $\text{[math]}$ 为等边三角形；
2. （2）如图2，当点E在 $\text{[math]}$ 的延长线上时，求证： $\text{[math]}$ 为等腰三角形．
答案解析收藏纠错 + 选题
18. (2024八上·道里期末) 点D为 $\text{[math]}$ 的边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，点E在 $\text{[math]}$ 外，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，若 $\text{[math]}$ ，请你判定 $\text{[math]}$ 的形状并证明；
2. （2）如图2，若 $\text{[math]}$ ，请你判定 $\text{[math]}$ 的形状并证明．
答案解析收藏纠错 + 选题
19. (2023八上·松原期中) △ABC中，AB=AC，点D为射线BC上一个动点（不与B，C重合），以AD为一边向AD的左侧作△ADE，使AD=AE，∠DAE=∠BAC，过点E作BC的平行线，交直线AB于点F，连接BE．
1. （1）如图①，若∠BAC=∠DAE=60°，则△BEF是三角形；
2. （2）若∠BAC=∠DAE≠60°
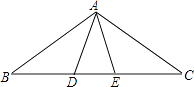
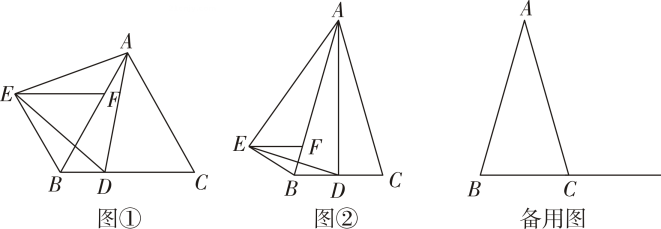
  ①如图②，当点D在线段BC上移动，判断△BEF的形状并证明；
  ②当点D在线段BC的延长线上移动，△BEF是什么三角形？请直接写出结论并画出相应的图形．
答案解析收藏纠错 + 选题
20. (2024八上·斗门期末) 在等边 $\text{[math]}$ 中，点 $\text{[math]}$ 为边 $\text{[math]}$ 上任意一点，点 $\text{[math]}$ 在边 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．
1. （1）如图1，若点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，求证： $\text{[math]}$ ；
2. （2）如图2，若点 $\text{[math]}$ 为 $\text{[math]}$ 上任意一点，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题

四、实践探究题

21. (2023八上·哈尔滨期中) 数学课上，刘老师出示了如下的题目：如图1，在等边 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，试确定线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，并说明理由.
小敏与同桌小聪探究解答的思路如下：
1. （1）特殊情况，探索结论：
  当点 $\text{[math]}$ 为 $\text{[math]}$ 的中点时，如图2，确定线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，请你直接写出结论： $\text{[math]}$ $\text{[math]}$ （填“>”或填“<”或填“=”）
2. （2）特例启发，解答题目：
  解：题目中， $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是： $\text{[math]}$ $\text{[math]}$ （填“>”或填“<”或填“=”）.
  理由如下：如图3，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .（请你补充完成解答过程）
3. （3）拓展结论，设计新题：
  小敏解答后，提出了新的问题：在等边 $\text{[math]}$ 中，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，且 $\text{[math]}$ ，已知 $\text{[math]}$ 的边长为3， $\text{[math]}$ ，则 $\text{[math]}$ 的长=（请直接写出结果，备用图供选用）.
答案解析收藏纠错 + 选题

五、综合题

22. (2023七下·闵行期末) 已知在等边 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一点，点 $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点， $\text{[math]}$ ．
1. （1）如图1，如果点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，说明 $\text{[math]}$ ；
2. （2）如图2，如果点 $\text{[math]}$ 是 $\text{[math]}$ 上任意一点（不与点 $\text{[math]}$ 、 $\text{[math]}$ 重合）， $\text{[math]}$ 还成立吗？请说明理由．
答案解析收藏纠错 + 选题
23. (2023八上·宁波期末) 两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形．如图1，在“手拉手”图形中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连结BD，CE，则△ABD≌△ACE．
1. （1）请证明图1的结论成立；
2. （2）如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，求∠BOC的度数；
3. （3）如图3，AB＝BC，∠ABC＝∠BDC＝60°，试探究∠A与∠C的数量关系．
答案解析收藏纠错 + 选题
24. (2023八上·桂平期末) 如图，已知点D是等边三角形 $\text{[math]}$ 中 $\text{[math]}$ 边所在直线上的点，连接 $\text{[math]}$ ，过点D作 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的邻补角的平分线交于点F.
1. （1）如图①，当点D在线段 $\text{[math]}$ 上时，过点D作 $\text{[math]}$ ，且交 $\text{[math]}$ 于点E.求证： $\text{[math]}$ ；
2. （2）如图①，在（1）的条件下，求证： $\text{[math]}$ ；
3. （3）如图②，当点D在线段 $\text{[math]}$ 的延长线上时，（2）中线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系式还成立吗？若成立，请加以证明；若不成立，请写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间新的数量关系式，并说明理由.
答案解析收藏纠错 + 选题