《圆》精选压轴题—2024年浙教版数学九（上）期中复习

更新时间：2024-10-21 浏览次数：15 类型：复习试卷

一、选择題

1. (2023九上·玉环期中) 如图，⊙O是△ABC的外接圆，弦BD交AC于点E，AE=DE，BC=CE，过点O作OF⊥AC于点F，延长FO交BE于点G，若DE=6，EG=4，则AB的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 13 D . 14

答案解析收藏纠错 + 选题
2. (2024九上·杭州期中) 如图，在△ABC中，AD是BC边上的高，⊙P是△ABC的外接圆，连接PA ．若AD＝3，BD＝1，BC＝5，则PA的长（）

A . 2.5 B . $\text{[math]}$ C . $\text{[math]}$ D . 2.8

答案解析收藏纠错 + 选题
3. (2023九上·乐清期中) 已知点A ， B ， C在⊙O上，∠ABC＝30°，把劣弧 $\text{[math]}$ 沿着直线CB折叠交弦AB于点D ．若BD＝9，AD＝6，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 3π C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·温州期中) 阿基米德折弦定理：如图1，AB与BC是 $\text{[math]}$ 的两条弦(即折线ABC是圆的一条折弦)，AB>BC，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点 $\text{[math]}$ ，则点 $\text{[math]}$ 是折弦ABC的中点，即 $\text{[math]}$ .如图2，半径为4的圆中有一个内接矩形 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点 $\text{[math]}$ ，若矩形ABCD的面积为20，则线段BN的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·乐清期中) 已知点A，B，C在⊙O上，∠ABC=30°，把劣弧 $\text{[math]}$ 沿着直线CB折叠交弦AB于点D．若BD=9，AD=6，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ π B . 3π C . $\text{[math]}$ π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
6. (2023九上·绍兴期中) 如图，在边长为8的正方形 $\text{[math]}$ 中，点O为正方形的中心，点E为 $\text{[math]}$ 边上的动点，连结 $\text{[math]}$ ，作 $\text{[math]}$ 交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ ， P为 $\text{[math]}$ 的中点，G为边 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 10 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·浙江期中) 量角器和三角板是我们平常数学学习中常用的工具．有一天，爱思考的小聪拿着两块工具拼成了如图1的样子，计划让三角板的直角顶点始终在量角器的半圆弧上运动，紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点，点P为三角板的直角顶点，两直角边PE、PF分别过点A、B．连结CP，过点O作OM⊥CP交CP于点M，交AP于点N若AB=8，则NB的最小值为；若点Q为 $\text{[math]}$ 的中点，则点P从点Q运动到点B时，N点的运动路径长为.

答案解析收藏纠错 + 选题
8. (2023九上·杭州期中) 如图，点O在线段AB上，OA＝2，OB＝6，以O为圆心，OA为半径作⊙O，点M在⊙O上运动，连结MB，以MB为一边作等边△MBC，连结AC，则AC长度的最小值为（）

A . 2 $\text{[math]}$ 2 B . 2 $\text{[math]}$ 2 C . 4 $\text{[math]}$ 2 D . 4 $\text{[math]}$ 2

答案解析收藏纠错 + 选题
9. (2023九上·仙居期中) 如图，正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 上，顶点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 内，将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上．若正方形 $\text{[math]}$ 的边长和 $\text{[math]}$ 的半径相等，则旋转角度 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·绍兴期中) 如图，在半圆O中，直径AB＝2，C是半圆上一点，将弧AC沿弦AC折叠交AB于D ，点E是弧AD的中点．连接OE ，则OE的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·乐清期中) 如图，点P是线段AB上一动点（不包括端点），过点P作PQ⊥AB交以AB为直径的半圆O于点Q ，连接AQ ，过点P作PC∥AQ交该半圆于点C ，连接CB ．当△PCB是以PC为腰的等腰三角形时， $\text{[math]}$ 为．

答案解析收藏纠错 + 选题
12. (2023九上·上城期中) 如图，在以AB为直径的半圆O上，AB＝2 $\text{[math]}$ ，点C事半圆弧上的任务点，点F是 $\text{[math]}$ 的中点，连接BF交AC于点E，AD平分∠CAB交BF于点D，则∠ADB＝度；当DB＝DF时，BC的长为．

答案解析收藏纠错 + 选题
13. (2023九上·温岭期中) 如图，在平面直角坐标系中，点P是以C（-1.5，2）为圆心，1为半径的⊙C上的一个动点，已知A（﹣1，0），B（1，0），连接PA ， PB ，则PA²+PB²的最小值是．

答案解析收藏纠错 + 选题
14. (2023九上·乐清期中) 如图，点P是线段AB上一动点(不包括端点)，过点P作PQ⊥AB交以AB为直径的半圆O于点Q，连结AQ，过点P作PC∥AQ交该半圆于点C，连结CB．当△PCB是以PC为腰的等腰三角形时， $\text{[math]}$ 为

答案解析收藏纠错 + 选题
15. (2023九上·仙居期中) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上移动，连接 $\text{[math]}$ ，并将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，连接 $\text{[math]}$ 在点 $\text{[math]}$ 移动的过程中， $\text{[math]}$ 长度的最小值为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023九上·洞头期中) 图1是某游乐园的摩天轮，A，B两位同学坐在摩天轮上的示意图如图2，摩天轮半径OA为9米，两同学的直线距离AB为6米，当两位同学旋转到同一高度时（A在B的右侧），A同学距离地面的高度为米，当A同学旋转到最高位置，此时两位同学的高度差为米．

答案解析收藏纠错 + 选题
17. (2023九上·绍兴期中) 如图，已知在⊙O中，AB是⊙O的直径，AC＝4，BC＝3．若D为⊙O上一点，且△ABD为等腰三角形，则弦CD的长为．

答案解析收藏纠错 + 选题

三、解答题

18. (2023九上·杭州期中)
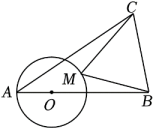
已知：如图1，四边形ABCD内接于 $\text{[math]}$ O，AC⊥BD于点P，F为BC延长线上一点．
1. （1）求证：∠DCF=∠DAB
2. （2）过O作OE⊥AB于点E(如图2)，试猜想线段OE与DC的数量关系，并证明你的猜想.
3. （3）当图2中点P运动到圆外时，即AC、BD的延长线交于点P，且∠P=90°时 $\text{[math]}$ 如图 $\text{[math]}$ 所示 $\text{[math]}$ ，（2）中的猜想是否成立？如果成立请给出你的证明，如果不成立请说明理由．
答案解析收藏纠错 + 选题
19. (2023九上·期中) 如图1，AB为⊙O的直径，CD⊥AB于点E ， $\text{[math]}$ ， BF与CD交于点G ．
1. （1）求证：CD＝BF ．
2. （2）若BE＝1，BF＝4，求GE的长．
3. （3）连结GO ， OF ，如图2，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023九上·余姚期中) 在平面直角坐标系xOy中，已知点P（4，3），⊙O经过点P，过点P作x轴的平行线交⊙O于点E.
1. （1）如图1，求线段OP的长；
2. （2）点A为y轴正半轴上的一动点，点B和点A关于直线PE对称，连接PA，PB.直线PA，PB分别交⊙O于点C，D.直线CD交x轴于点F，交直线PE于点G.
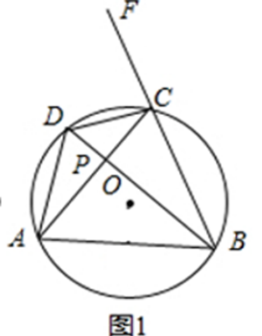
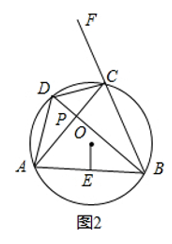
  ①点A运动到如图2位置，连接CE，DE.求证：∠DGP= $\text{[math]}$ ECP.
  
  ②在点A运动过程中，当DF=OP时，求点D的坐标.
答案解析收藏纠错 + 选题
21. (2023九上·绍兴期中) 如图，在△ABC中，AB＝BC，∠ABC＝90°，D是AB上一动点，连接CD，以CD为直径的⊙M交AC于点E，连接BM并延长交AC于点F，交⊙M于点G，连接BE．
1. （1）求证：点B在⊙M上．
2. （2）当点D移动到使CD⊥BE时，求BC：BD的值．
3. （3）求证：AE²+CF²＝EF² ．
答案解析收藏纠错 + 选题
22. (2023九上·浙江期中) 如图1，△ABC是⊙O内接三角形将△ABC绕点A逆时针旋转至△AED，其中点D在圆上，点E在线段AC上．
1. （1）求证：DE=DC；
2. （2）如图2，过点B作BF∥CD分别交AC、AD于点M、N，交⊙O于点F，连结AF．求证：AN·DE=AF·BM：
3. （3）在(2)的条件下，若 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2023九上·安吉期中) 已知⊙O为△ABC的外接圆，AB＝BC．
1. （1）如图1，连结OB交AC于点E，过A作CO的垂线交CO延长线于点D．
  ①求证：BO平分∠ABC；
  ②设∠ACB＝α，∠DAC＝β，请用含α的代数式表示β；（直接写出答案）
2. （2）如图2，若∠ABC＝90°，F为⊙O上的一点，且点B，F位于AC两侧，作△ABF关于AB对称的图形△ABG，连结GC，试猜想AG，CG，BG三者之间的数量关系并给予证明．
答案解析收藏纠错 + 选题
24. (2023九上·余杭期中) 如图，△ABC内接于⊙O，过点O作OH⊥BC于点H，延长OH交⊙O于点D，连接AD、BD，AD与BC交于点E，AD＝9．
1. （1）求证：∠BAD＝∠CAD．
2. （2）若OH＝DH．
  ①求∠BAC的度数．
  ②若⊙O的半径为6，求DE的长．
3. （3）设BD＝x，AB⋅CE＝y，求y关于x的函数表达式．
答案解析收藏纠错 + 选题
25. (2023九上·上城期中) 如图1，四边形ABDE内接于⊙O，AB＝AE，AC⊥BD于点F．点C在⊙O上，AC⊥BD于点F.
1. （1）连接BE，求证：∠ABE＝∠ACB．
2. （2）设∠CBF为x度，∠BAE为y度，写出y关于x的函数表达式．
3. （3）如图2，作OG⊥AC于点G，连接AO并延长交⊙O于点H．
  ①∠BAE＝120°，OG＝4， $\text{[math]}$ ，求BD的长．
  ②若DE＝12，求OG的长．
答案解析收藏纠错 + 选题
26. (2023九上·义乌期中) 如图1，在Rt△ABC中，∠ABC＝90°，∠C＝30°，BC＝12，D是BC的中点．经过A ， B ， D的⊙O交AC于E点．
1. （1）求AE的长．
2. （2）当点P从点A匀速运动到点E时，点Q恰好从点C匀速运动点B ．记AP＝x ， BQ＝y ．
  ①求y关于x的表达式．
  ②连结PQ ，当△PQC的面积最大时，求x的值．
3. （3）如图2，连结BE ， BP ，延长BP交⊙O于点F ，连结FE ．当EF与△BDE中的某一边相等时，求四边形BDEF的面积．
答案解析收藏纠错 + 选题
27. (2023九上·洞头期中) 如图，
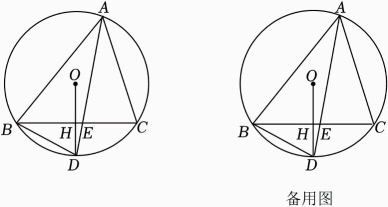
在△ABC中，AB＝BC，∠ABC＝90°，D是AB上一动点，连接CD，以CD为直径的⊙O交AC于点E，连接BO并延长交AC于点F，交⊙O于点G，连接BE，EG．
1. （1）求证：BE＝EG．
2. （2）当CD平分∠BCA时，求证：△BEF为等腰三角形．
3. （3）当BD＝CF，请直接写出△COF和△BOD的面积之比为．
答案解析收藏纠错 + 选题
28. (2023九上·温岭期中) 如图1，扇形AOB中，∠AOB＝90°，OA＝6，点P在半径OB上，连接AP ．
1. （1）把△AOP沿AP翻折，点O的对称点为点Q ．
  ①当点Q刚好落在弧AB上，求弧AQ的长；
  ②如图2，点Q落在扇形AOB外，AQ与弧AB交于点C ，过点Q作QH⊥OA ，垂足为H ，
  探究OH、AH、QC之间的数量关系，并说明理由；
2. （2）如图3，记扇形AOB在直线AP上方的部分为图形W ，把图形W沿着AP翻折，点B的对称点为点E ，弧AE与OA交于点F ，若OF＝2，求PO的长．
答案解析收藏纠错 + 选题