题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

浙教版数学九上第4章相似三角形优生综合题特训

更新时间：2021-11-13 浏览次数：167 类型：复习试卷

一、综合题

1. (2021·黄埔模拟) 如图1所示，点C把线段 $\text{[math]}$ 分成 $\text{[math]}$ 与 $\text{[math]}$ ，若 $\text{[math]}$ ，则称线段 $\text{[math]}$ 被点C黄金分割（goldensection），点C叫做线段 $\text{[math]}$ 的黄金分割点， $\text{[math]}$ 与 $\text{[math]}$ 的比叫做黄金比．
1. （1）根据上述定义求黄金比；
2. （2）在图2中，利用尺规按以下步骤作图，井保留作图痕迹．①作线段 $\text{[math]}$ 的垂直平分线，得线段 $\text{[math]}$ 的中点M；②过点B作 $\text{[math]}$ 垂线l；③以点B为圆心，以 $\text{[math]}$ 为半径作圆交l于N；④连接 $\text{[math]}$ 、 $\text{[math]}$ ，以N为圆心，以 $\text{[math]}$ 为半径作圆交 $\text{[math]}$ 于P；⑤以点A为圆心，以 $\text{[math]}$ 为半径作圆交 $\text{[math]}$ 于C ．
3. （3）证明你按以上步骤作出的C点就是线段 $\text{[math]}$ 的黄金分割点．
答案解析收藏纠错 + 选题
2. (2020九上·湖北月考) 定义：如图1，点P为线段AB上一点，如果 $\text{[math]}$ =k，那么我们称点P是线段AB的黄金分割点， $\text{[math]}$ 叫做黄金分割数.
1. （1）理解：利用图1，运用一元二次方程的知识，求证：黄金分割数 $\text{[math]}$ ；
2. （2）应用：如图2，抛物线y＝x²+nx＋2n（n<0）的图象与x轴交于A、B两点（OA<OB），若原点O是线段AB的黄金分割点，①求线段AB的长；②直接写出点A和点B的坐标.
答案解析收藏纠错 + 选题
3. 如图，在一块长为a(cm)，宽为b(cm)(a>b)的矩形黑板的四周，镶上宽为x(cm)的木板，得到一个新的矩形．
1. （1）试用含a，b，x的代数式表示新矩形的长和宽；
2. （2）试判断原矩形的长、宽与新矩形的长、宽是不是比例线段，并说明理由．
答案解析收藏纠错 + 选题
4. 已知线段a，b，c满足 $\text{[math]}$ ，且a＋2b＋c＝26.
1. （1）判断a，2b，c，b²是否成比例；
2. （2）若实数x为a，b的比例中项，求x的值．
答案解析收藏纠错 + 选题
5. (2021·玄武模拟) （问题情境）
如图①，小区 $\text{[math]}$ 、 $\text{[math]}$ 位于一条笔直的道路 $\text{[math]}$ 的同侧，为了方便 $\text{[math]}$ ， $\text{[math]}$ 两个小区居民投放垃圾，现在 $\text{[math]}$ 上建一个垃圾分类站 $\text{[math]}$ ，使得 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 的距离之比为 $\text{[math]}$ .
1. （1）（初步研究）
  在线段 $\text{[math]}$ 上作出点 $\text{[math]}$ ，使 $\text{[math]}$ .
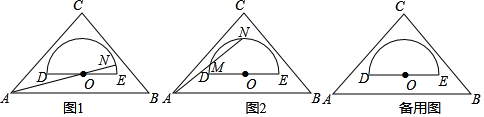
  如图，做法如下：
  
  第一步：过点 $\text{[math]}$ 作射线 $\text{[math]}$ ，
  
  以 $\text{[math]}$ 为圆心，任意长为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ；
  
  以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ；
  
  以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ .
  
  第二步：连接 $\text{[math]}$ ，作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .
  
  则点 $\text{[math]}$ 即为所求.
  
  请证明所作的点 $\text{[math]}$ 满足 $\text{[math]}$ .
2. （2）（深入思考）
  如图，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 外，且 $\text{[math]}$ .
  求证： $\text{[math]}$ 是 $\text{[math]}$ 的平分线.
3. （3）（问题解决）
  如图，已知点 $\text{[math]}$ ， $\text{[math]}$ 和直线 $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ .用直尺和圆规完成下列作图.（保留作图痕迹，不写作法）
  （ⅰ）在直线 $\text{[math]}$ 上作出点 $\text{[math]}$ （异于点 $\text{[math]}$ ），使 $\text{[math]}$ ；
  
  （ⅱ）在直线 $\text{[math]}$ 上作出点 $\text{[math]}$ ，使 $\text{[math]}$ .
答案解析收藏纠错 + 选题
6. (2021·余杭模拟) 如图，已知等边 $\text{[math]}$ ，在 $\text{[math]}$ ， $\text{[math]}$ 边分别取点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ≌ $\text{[math]}$ .
2. （2）若 $\text{[math]}$ .
  ①求 $\text{[math]}$ 的值.
  
  ②设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
7. (2022九下·成都月考) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ ： $\text{[math]}$ 经过点 $\text{[math]}$ 和 $\text{[math]}$ .
1. （1）求抛物线 $\text{[math]}$ 的对称轴.
2. （2）当 $\text{[math]}$ 时，将抛物线 $\text{[math]}$ 向左平移2个单位，再向下平移1个单位，得到抛物线 $\text{[math]}$ .
  ①求抛物线 $\text{[math]}$ 的解析式.
  
  ②设抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，连接 $\text{[math]}$ .点 $\text{[math]}$ 为第一象限内抛物线 $\text{[math]}$ 上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ .设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ .是否存在点 $\text{[math]}$ ，使得以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似，若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
8. (2021·张店模拟) 已知一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象在第一象限交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求反比例函数与一次函数的解析式；
2. （2）直接写出 $\text{[math]}$ 的解集；
3. （3）若点 $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，求使 $\text{[math]}$ 的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
9. (2021九上·渭滨期末) 综合问题：从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线.
1. （1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线.
2. （2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数.
3. （3）如图2，△ABC中，AC=2，DC= $\text{[math]}$ - $\text{[math]}$ ，BD= $\text{[math]}$ ，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求CB长.
答案解析收藏纠错 + 选题
10. (2021·三台模拟) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 、 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，且点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）求一次函数和反比例函数的表达式.
2. （2）求 $\text{[math]}$ 的面积.
3. （3）点 $\text{[math]}$ 为反比例函数图象上的一个动点， $\text{[math]}$ 轴于 $\text{[math]}$ ，是否存在以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似，若存在，直接写出 $\text{[math]}$ 点的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题
11. (2020九上·阆中月考) 如图所示，在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，动点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点．将线段 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针方向旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ ，连结 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）写出点 $\text{[math]}$ 的坐标；
2. （2）当 $\text{[math]}$ 时，试问：以 $\text{[math]}$ 为顶点的四边形能否为平行四边形？若能，求出相应的 $\text{[math]}$ 的值？若不能，请说明理由；
3. （3）当 $\text{[math]}$ 为何值时，△ $\text{[math]}$ 与△ $\text{[math]}$ 相似？
答案解析收藏纠错 + 选题
12. (2020九上·高新月考) 如图，平行四边形ABCD在平面直角坐标系中，AD＝6，若OA、OB的长是关于x的一元二次方程x²﹣7x+12＝0的两个根，且OA＞OB．
1. （1）求 $\text{[math]}$ 的值．
2. （2）若E为x轴上的点，且S_△_AOE＝ $\text{[math]}$ ，求经过D、E两点的直线的解析式，并判断△AOE与△DAO是否相似？
3. （3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
13. (2020九上·长沙月考) 在平面直角坐标系中，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与 $\text{[math]}$ 轴的两个交点分别为A、B，与 $\text{[math]}$ 轴相交于点C，点A（ $\text{[math]}$ ，0）， $\text{[math]}$ ，连接BC，tan∠OCB=2．
1. （1）求该抛物线的解析式；
2. （2）设点P是抛物线上在第一象限内的动点（不与C、B重合），过点P做PD⊥BC，垂足为点D．
  ①点P在运动过程中，线段PD的长度是否存在最大值？若存在，请求出点D的坐标；若不存在，请说明理由；
  
  ②以P、D、C为顶点的三角形与△COA相似时，求出点P的坐标．
答案解析收藏纠错 + 选题
14. (2021九上·哈尔滨月考) 如图在平面直角坐标系中，点O为坐标原点，直线y $\text{[math]}$ x+b分别交x轴，y轴于点A、B ， OA＝4，∠OBA的外角平分线交x轴于点D ．
1. （1）求点D的坐标；
2. （2）点P是线段BD上一点（不与B、D重合），过点P作PC⊥BD交x轴于点C ，设点P的横坐标为t ， △BCD的面积为S ，求S与t之间的函数解析式（不要求写出自变量t的取值范围）；
3. （3）在（2）的条件下，PC的延长线交y轴于点E ，当PC＝PB时，将射线EP绕点E旋转45°交直线AB于点F ，求F点坐标．
答案解析收藏纠错 + 选题
15. (2021九上·成都开学考) 已知正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一点（不与 $\text{[math]}$ 、 $\text{[math]}$ 重合），将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，如图1，连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3）如图2，当点 $\text{[math]}$ 是边 $\text{[math]}$ 的中点时， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
16. (2021九上·渝中开学考) 如图，已知抛物线 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，抛物线的对称轴与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .点 $\text{[math]}$ 从 $\text{[math]}$ 点出发，以每秒1个单位长度的速度向 $\text{[math]}$ 运动，过 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，交抛物线于点 $\text{[math]}$ ，交 $\text{[math]}$ 于 $\text{[math]}$ .
1. （1）求点 $\text{[math]}$ 和点 $\text{[math]}$ 的坐标；
2. （2）设当点 $\text{[math]}$ 运动了 $\text{[math]}$ （秒 $\text{[math]}$ 时，四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式，并指出自变量 $\text{[math]}$ 的取值范围；
3. （3）在线段 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 成为以 $\text{[math]}$ 为一腰的等腰三角形？若存在，求出点 $\text{[math]}$ 的坐标，若不存在，说明理由.
答案解析收藏纠错 + 选题
17. (2021·鼓楼模拟) 学完“探索三角形相似的条件”之后，小明所在的学习小组尝试探索四边形相似的条件，以下是他们的思考，请你和他们一起完成探究过程.
（定义）四边成比例，且四角分别相等的两个四边形叫做相似四边形.
1. （1）（初步思考）
  小明根据探索三角形相似的条件所获得的经验，考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”，“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件，于是，可以从“四边成比例，且一角对应相等的两个四边形相似”，“三边成比例，且两角分别相等的两个四边形相似”，“两边成比例，且三角分别相等的两个四边形相似”来探究.
2. （2）（深入探究）
  学习小组一致认为，“四边成比例，且一角对应相等的两个四边形相似”是真命题，请结合图形完成证明.
  
  已知：四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .
  
  求证：四边形 $\text{[math]}$ 四边形 $\text{[math]}$ .证明：
3. （3）对于“三边成比例，且两角分别相等的两个四边形相似”，学习小组得到如下的四个命题：
  ①“三边成比例，两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”；
  
  ②“三边成比例，两邻角分别相等且都不是其中两边的夹角的两个四边形相似”；
  
  ③“三边成比例及其两夹角分别相等的两个四边形相似”；
  
  ④“三边成比例，两对角分别相等的两个四边形相似”.
  
  其中真命题是.（填写所有真命题的序号）
4. （4）请你完成“两边成比例，且三角分别相等的两个四边形相似”的探究过程.
答案解析收藏纠错 + 选题
18. (2021·邵阳模拟) 如图所示，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，其对称轴 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为抛物线的顶点.
1. （1）求抛物线的表达式.
2. （2）若直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，求证： $\text{[math]}$ .
3. （3）若点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点，是否存在以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似.若存在，求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
19. (2022九下·海曙开学考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，P是斜边 $\text{[math]}$ 上一个动点，以 $\text{[math]}$ 为直径作 $\text{[math]}$ 交 $\text{[math]}$ 于点D，与 $\text{[math]}$ 的另一个交点E，连接 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，
  ①若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
  
  ②求证 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ 时，是否存在点P，使得 $\text{[math]}$ 是等腰三角形，若存在，求出所有符合条件的 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
20. (2022八下·东营期末) 如图，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$
①以点 $\text{[math]}$ 为旋转中心，将 $\text{[math]}$ 顺时针方向旋转90°，得到 $\text{[math]}$ ；

②以点 $\text{[math]}$ 为位似中心，将 $\text{[math]}$ 放大 $\text{[math]}$ ，使相似比为 $\text{[math]}$ ，且点 $\text{[math]}$ 在第三象限．
1. （1）在图中画出 $\text{[math]}$ 和 $\text{[math]}$ ；
2. （2）请直接写出点 $\text{[math]}$ 的坐标：（，）
3. （3）在上面的（2）问下，直接写出在线段 $\text{[math]}$ 上的任意动点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标：（，）．
答案解析收藏纠错 + 选题
21. (2020九上·惠山月考) （1）在正方形方格纸中，我们把顶点均在“格点”上的三角形称为“格点三角形”，如图△ABC是一个格点三角形，点A的坐标为（-2，2）.
1. （1）点B的坐标为，△ABC的面积为；
2. （2）在所给的方格纸中，请你以原点O为位似中心，将△ABC缩小为原来的一半（仅用直尺）；
3. （3）在（2）中，若P（a，b）为线段AC上的任一点，则缩小后点P的对应点P₁的坐标为.
4. （4）按要求作图，不要求写作法，但要保留作图痕迹.
  我们知道，三角形具有性质：三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高所在直线相交于一点.
  
  请运用上述性质，只用直尺（不带刻度）作图.
  
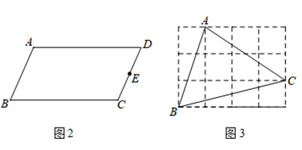
  ①如图2，在平行四边形ABCD中，E为CD的中点，作BC的中点F.
  
  ②如图3，在由小正方形组成的4×3的网格中，△ABC的顶点都在小正方形的顶点上，作△ABC的高AH.
答案解析收藏纠错 + 选题
22. (2021九上·贵州期末) 如图所示，身高1.5米的小明从路灯下的A点经过，测量得身后的影子 $\text{[math]}$ 的长5米，沿 $\text{[math]}$ 所在的直线行走10米到B点时，身后的影子 $\text{[math]}$ 长为2米.
1. （1）请你确定路灯P的位置
2. （2）求路灯P距到地面的距离.
答案解析收藏纠错 + 选题

23. (2021九下·盐城月考) 以下是一个合作学习小组在一次数学实验中的过程记录，请阅读后完成下列问题.

（1）（度量操作）

如图1，AB⊥PQ ，垂足为A，AB=3，E为射线AQ上一个动点（点E与点A不重合），∠AEB=∠BEC，BC⊥BE，过点C作CD⊥PQ，垂足为点D.在探究线段AB、线段AE、线段AD三者之间的关系时，通过画图、度量，收集到一组数据如下表：（单位：cm）

AE	1	1.5	1.8	2	2.25	3	4	4.5	5
AD	9	6	5	4.5	4	3	2.25	2	1.8

根据学习函数的经验，选取上表中 $\text{[math]}$ 和 $\text{[math]}$ 的数据进行分析：

①设 $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为坐标，在图2所示的坐标系中描出对应的点；

②连线.

（2）（观察思考）
结合表中的数据，猜想：当AB=3时， $\text{[math]}$ .
（3）进一步猜想：AB⊥PQ，垂足为A，E为射线AQ上一个动点（点E与点A不重合），∠AEB=∠BEC，BC⊥BE，过点C作CD⊥PQ，垂足为点D.则线段AB、AE、AD三者之间的关系为.
（4）（推理证明）
请利用图1证明上述（4）中的猜想.
（5）（逆向运用）
如图3为一张四边形ABCD纸片，∠BAD=∠ADC=90°， $\text{[math]}$ ， AD=2，请通过折纸的方法在AD边上找一个点E，使得BE平分∠AEC.（答题要求：简单叙述折纸的方法即可，不需要证明.）

图3

答案解析收藏纠错 + 选题

24. (2022九上·新昌月考) 如图1是一块内置量角器的等腰直角三角板，它是一个轴对称图形.已知量角器所在的半圆O的直径DE与AB之间的距离为1，DE＝4，AB＝8，点N为半圆O上的一个动点，连结AN交半圆或直径DE于点M.
1. （1）当AN经过圆心O时，求AN的长；
2. （2）如图2，若N为量角器上表示刻度为90°的点，求△MON的周长；
3. （3）当 $\text{[math]}$ 时，求△MON的面积.
答案解析收藏纠错 + 选题

试卷信息