浙教版初中数学八下第四章平行四边形优生加练-在线组卷

1. 如图所示，在 $\text{[math]}$ 中，过对角线BD上一点 $\text{[math]}$ 作 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；
（2）若 $\text{[math]}$ ，求四边形AEPH的面积.

答案解析收藏纠错 + 选题

2. 如图，在△ABC中，点D，E分别是边AB，BC的中点，点F，G是边AC的三等分点，DF，EG的延长线相交于点H.

求证：

（1） DF//BG，DF= $\text{[math]}$ BG；
（2）四边形FBGH是平行四边形；
（3）四边形ABCH是平行四边形.

答案解析收藏纠错 + 选题

3. 如图，在△ABC中，AB=AC，点M在BA的延长线上.

（1）按下列要求作图，并在图中标明相应的字母.①作∠CAM的平分线AN；②作AC的中点О，连结BO，并延长BO交AN于点D，连结CD.
（2）在(1)的条件下，判断四边形ABCD的形状，并证明你的结论.

答案解析收藏纠错 + 选题

4. 已知在四边形ABCD中， $\text{[math]}$ $\text{[math]}$ .

（1） $\text{[math]}$ (用含 $\text{[math]}$ 的代数式直接填空)；
（2）如图1，若x=y=90°，DE平分∠ADC，BF平分∠CBM，DE与BC交于点G，
求证：DE⊥BF；
（3）如图2，∠DFB为四边形ABCD的∠ABC，ADC相邻的外角平分线所在直线构成的锐角.若x+y=120°，∠DFB=20°，请直接写出x，y的值.

答案解析收藏纠错 + 选题

5. (2021八上·西湖期中) 如图，在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，若动点P从点C开始，按C→A→B的路径运动，且速度为每秒2cm，设点P的运动时间为t秒.

（1）则AC＝cm；
（2）当BP平分∠ABC，求此时点P的运动时间t的值；
（3）点P运动过程中，△BCP能否成为等腰三角形？若能，求出t的值；若不能请说明理由.

答案解析收藏纠错 + 选题

6. (2021八上·拱墅期中) 如图1，△ABC中，BE平分∠ABC交AC边于点E，过点E作DE∥BC交AB于点D，

（1）求证：△BDE为等腰三角形；
（2）若点D为AB中点，AB＝6，求线段BC的长；
（3）在图2条件下，若∠BAC＝60°，动点P从点B出发，以每秒1个单位的速度沿射线BE运动，请直接写出图3当△ABP为等腰三角形时t的值.

答案解析收藏纠错 + 选题

7. (2021八上·下城期中) 如图，在Rt△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒1个单位长度.

（1）当t＝2时，分别求CD和AD的长；
（2）当t为何值时，△CBD是直角三角形？
（3）若△CBD是等腰三角形，请直接写出t的值.

答案解析收藏纠错 + 选题

8. (2021九上·温州开学考) 如图，在直角坐标系中直线AB与x、y轴分别交于点A、B两点，已知B(0，4)，∠BAO=30°，P，Q分别是线段OB，AB上的两个动点，点P从O出发以每秒3个单位长度的速度向终点B运动，点Q从B出发以每秒8个单位长度的速度向终点A运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为t（秒）

（1）求点A的坐标和线段AB的长；
（2）当t为何值时，△BPQ的面积为2 $\text{[math]}$ ；
（3）若C为OA的中点，连结QC，QP，以QC，QP为邻边作平行四边形PQCD，
①t为何值时，点D恰好落在坐标轴上；
②是否存在这样的 $\text{[math]}$ ，使x轴将平行四边形PQCD的面积分成1：3的两部分，若存在，请直接写出 $\text{[math]}$ 的值。

答案解析收藏纠错 + 选题

9. (2021八下·温州期末) 如图1，四边形ABCD是平行四边形，点E在边AD上，连结BE，过点D作DF∥BE，交BC于点F，点G，H分别是BE，DF的中点，连结EH，GF。

（1）求证：四边形EGFH为平行四边形。
（2）若BC=10，AB=6，∠ABC=60°。
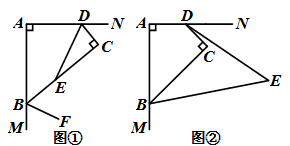
①当BG=GF时，求四边形EGFH的面积。

②如图2，延长FG交AB于点P，连结AG，记△APG的面积为S₁ ， △BPG的面积为S₂ ，若FP⊥AB，求 $\text{[math]}$ 的值。

答案解析收藏纠错 + 选题

10. (2021八下·苍南期末) 在直角坐标系xOy中，四边形ABCD是矩形，点A在x轴上，点C在y轴的正半轴上，点B，D分别在第一，二象限，且AB=3，BC=4。

（1）如图1，延长CD交x轴负半轴于点E，若AC=AE。
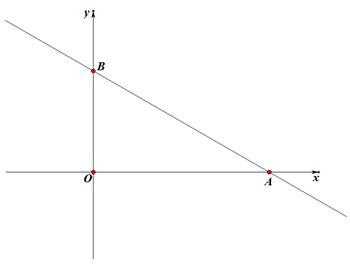
①求证：四边形ABDE为平行四边形。

②求点A的坐标。
（2）如图2，F为AB上一点，G为AD的中点，若点G恰好落在y轴上，且CG平分∠DCF，求AF的长。
（3）如图3，x轴负半轴上的点P与点Q关于直线AD对称，且AP=AD，若OBCQ的面积为矩形ABCD面积的 $\text{[math]}$ ，则BQ的长可为(写出所有可能的答案)。

答案解析收藏纠错 + 选题

11. (2021八下·椒江期末) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，引一条射线 $\text{[math]}$ ，使得 $\text{[math]}$ 平分 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，过 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一点，使得 $\text{[math]}$ ，在线段 $\text{[math]}$ 上取点 $\text{[math]}$ 、 $\text{[math]}$ （点 $\text{[math]}$ 在 $\text{[math]}$ 之间）， $\text{[math]}$ ，且 $\text{[math]}$ ，当点 $\text{[math]}$ 从点 $\text{[math]}$ 匀速运动到点 $\text{[math]}$ 时，点 $\text{[math]}$ 恰好从点 $\text{[math]}$ 匀速运动到点 $\text{[math]}$ .记 $\text{[math]}$ ， $\text{[math]}$ ，已知 $\text{[math]}$ .

（1） $\text{[math]}$ ， $\text{[math]}$ ；
（2） ①判断 $\text{[math]}$ 和 $\text{[math]}$ 的位置关系，并说明理由；
②若 $\text{[math]}$ ，当 $\text{[math]}$ ▲ 时，四边形 $\text{[math]}$ 是平行四边形.
（3）如图2，若 $\text{[math]}$ ，
①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；

②若 $\text{[math]}$ ，求 $\text{[math]}$ 值.

答案解析收藏纠错 + 选题

12. (2021八下·上虞期末) 如图1，在矩形ABCD中，AB=4，BC=3，点E为边CD上一动点，连结AE，作点D关于直线AE的对称点F，连结EF，DF，CF，AF，DF与AE交于点G．

（1）若DE=2，求证：AE//CF．
（2）如图2，连结AC，BD，若点F在矩形ABCD的对角线上，求所有满足条件的DE的长．
（3）如图3，连结BF，当点F到矩形ABCD一个顶点的距离等于2时，请直接写出△BCF的面积．

答案解析收藏纠错 + 选题

13. (2021八下·湖州期中) 我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”.

（1）如图1，在四边形ABCD中，∠A+∠C＝270°，∠D＝30°，AB＝BC，求证：四边形ABCD是“准筝形”；
（2）小军同学研究 “准筝形”时，思索这样一道题：如图2，“准筝形”ABCD，AD＝BD，∠BAD＝∠BCD＝60°，BC＝5，CD＝3，求AC的长.
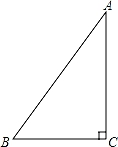
小军研究后发现，可以CD为边向外作等边三角形，构造手拉手全等模型，用转化的思想来求AC.请你按照小军的思路求AC的长.
（3）如图3，在△ABC中，∠A＝45°，∠ABC＝120°，BC＝2 $\text{[math]}$ ，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积.

答案解析收藏纠错 + 选题

14. (2021八上·上城期末) 如图，四边形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ 平分 $\text{[math]}$ 且 $\text{[math]}$ .

（1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
（2）求证： $\text{[math]}$ ；
（3）设 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作一条直线，分别与 $\text{[math]}$ ， $\text{[math]}$ 所在直线交于点 $\text{[math]}$ 点 $\text{[math]}$ .若 $\text{[math]}$ ，求 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的代数式表示）.

答案解析收藏纠错 + 选题

15. (2020八上·镇海期中) 如图，△ABC中，BA＝BC，CO⊥AB于点O，AO＝4，BO＝6.

（1）求BC，AC的长；
（2）若点D是射线OB上的一个动点，作DE⊥AC于点E，连结OE.
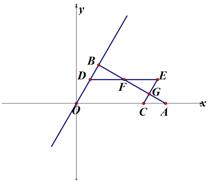
①当点D在线段OB上时，若△AOE是以AO为腰的等腰三角形，请求出所有符合条件的OD的长.

②设DE交直线BC于点F，连结OF，CD，若S_△_OBF：S_△_OCF＝1：4，则CD的长为（直接写出结果）.

答案解析收藏纠错 + 选题

16. (2020八下·镇海期末) 我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”.

（1）如图1，在四边形ABCD中，∠A+∠C＝270°，∠D＝30°，AB＝BC，求证：四边形ABCD是“准筝形”；
（2）如图2，在“准筝形”ABCD中，AB＝AD，∠BAD＝∠BCD＝60°，BC＝4，CD＝3，求AC的长；
（3）如图3，在△ABC中，∠A＝45°，∠ABC＝120°，AB＝3﹣ $\text{[math]}$ ，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积.

答案解析收藏纠错 + 选题

17. (2020八下·瑞安期中) 如图，在5×5的正方形网格中，每个小正方形的边长都是1，点A，B，C，D，E是五个格点，请在所给的网格中按下列要求画出图形.

（1）从所给的五个格点中选出其中四个作为顶点做一个平行四边形.
（2）过剩余一个点做一条直线l，使得直线l平分（1）小题中所做的平行四边形的面积.

答案解析收藏纠错 + 选题

18. (2020八下·温州期中) 如图：在平面直角坐标系中，点A在X轴的正半轴，OA=8 ，点B在第一象限，∠AOB=60°，AB⊥OB垂足为B，点D、C分别在边OB、OA上，且OD=AC=t，以OD、OC为边作平行四边形OCED，DE交直线AB为F，CE交直线AB为点G.

（1）当t=2时，则E的坐标为
（2）若ΔDFC的面积为 $\text{[math]}$ ，求t的值。
（3）当D、 B 、G、 E四点为顶点的四边形为平行四边形时，在Y轴上存在点M，过点M作FC的平行线交直线OB为点N，若以M、 N、 F、 C为顶点的四边形也是平行四边形，则点M的坐标为（直接写出答案）

答案解析收藏纠错 + 选题

19. (2020八下·温州期中) 如图1，在平面直角坐标系中，直线y= $\text{[math]}$ x+4与x轴、y轴分别交于点B，A。点P在线段OB上，且PB=m，点Q在直线AB上，Q的横坐标为m，连结PQ，以PQ，OQ作 $\text{[math]}$ PQOC。

（1）当m=3时，求点C的坐标；
（2）若 $\text{[math]}$ PQOC的面积等于18，求m的值；
（3）如图2，作点P关于原点O的对称点M，以BM为直角边在x轴下方作Rt△BMN，使得∠MBN=30°，∠BMN=90°，当点C恰好落在△BMN的一边上时，求m的值。

答案解析收藏纠错 + 选题

20. (2020八下·杭州期中) 在▱ABCD中，对角线AC，BD交于点O，且分别平分∠DAB，∠ABC。

（1）请求出∠AOB的度数，写出AD，AB，BC之间的等量关系，并给予证明。
（2）设点P为对角线AC上一点，PB=5，若AD+BC=16，四边形ABCD的面积为 $\text{[math]}$ ，求AP的长。

答案解析收藏纠错 + 选题

21. 如图，在四边形ABCD中，∠DAB＝90°，DB＝DC，点E，F分别为DB，BC的中点，连结AE，EF，AF.

（1）求证：AE＝EF；
（2）当AF＝AE时，设∠ADB＝α，∠CDB＝β，求α，β之间的数量关系．

答案解析收藏纠错 + 选题

22. (2019八下·吴兴期末) 如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8，以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E。

（1）求证：四边形ABCE是平行四边形；
（2）连接AC，BE交于点P，求AP的长及AP边上的高BH；
（3）在(2)的条件下，将四边形OABC置于如图所示的平面直角坐标系中，以E为坐标原点，其余条件不变，以AP为边向右上方作正方形APMN：
①求M点的坐标。
②直接写出正方形APMN与四边形OABC重叠部分的面积(图中阴影部分)

答案解析收藏纠错 + 选题

23. (2019八下·嘉兴期中) 已知在四边形ABCD中，∠A＝∠C＝90°．

（1） ∠ABC＋∠ADC＝°；
（2）如图①，若DE平分∠ADC，BF平分∠ABC的外角，请写出DE与BF的位置关系，并证明；
（3）如图②，若BE，DE分别四等分∠ABC、∠ADC的外角（即∠CDE＝ $\text{[math]}$ ∠CDN，∠CBE＝ $\text{[math]}$ ∠CBM），试求∠E的度数．

答案解析收藏纠错 + 选题

小学

初中

高中

浙教版初中数学八下第四章平行四边形优生加练

副标题：

*注意事项：

浙教版初中数学八下第四章平行四边形优生加练

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析