|
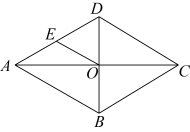
老师的问题: 已知:如图, 求作:菱形
|
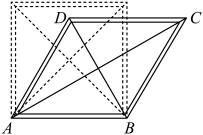
小明的作法: (1)以A为圆心, (2)以B为圆心, (3)连接 四边形
|
【解答问题】
请根据材料中的信息,证明四边形是菱形.
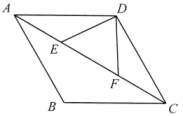


①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.

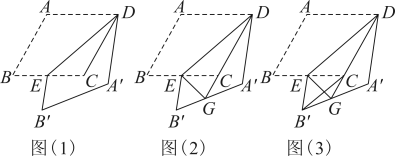
小南和小浦观察以上问题时,猜想 , 老师引导他们用“从特殊到一般”的思想方法去尝试研究.
②当时,
▲ .