, 其中
满足
, 取一个整数即可.
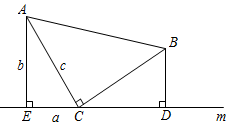
①求证: ;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
|
分组 |
频数 |
频率 |
|
4.5﹣22.5 |
2 |
0.050 |
|
22.5﹣30.5 |
3 |
|
|
30.5﹣38.5 |
10 |
0.250 |
|
38.5﹣46.5 |
19 |
|
|
46.5﹣54.5 |
5 |
0.125 |
|
54.5﹣62.5 |
1 |
0.025 |
|
合计 |
40 |
1.000 |

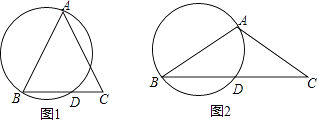

现规定:求若干个相同的有理数(均不等于0)的商的运算叫做除方,比如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2写作2③ , 读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)写作(﹣3)④ , 读作“(﹣3)的圈4次方”,一般地,把(a≠0)写作aⓝ , 读作“a的圈n次方”.
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

①若B、C两点关于y轴对称,求的值.
②求证:无论k为何值,为定值.
如图2,在 中,
为斜边,分别以
为斜边向外侧作
,若
,则面积
之间的关系式为;
如图3,在 中,
为斜边,分别以
为边向外侧作任意
,满足
,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论:若不成立,请说明理由;
如图4, 中,
,分别以它的三边向外作平行四边形,
交
于
交
于
,且
,若平行四边形
和平行四边形
的面积分别为
和
,则平行四边形
的面积为;

