
①如图2,当时,试判断重叠部分
的形状,并说明理由;
②如图3,当时,求重叠部分四边形
的面积(结果保留根号);
(参考数据:)
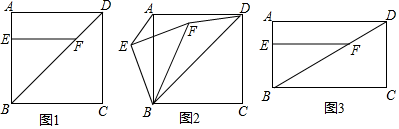
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:.
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=▲ °,∠CBQ=▲ °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
解答下列问题:

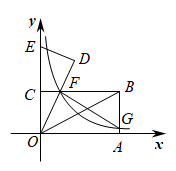
①如图2,当G、C、M三点共线时,设与
交于点N,求
的值;
②如图3,取中点P,连接
, 求
长度的最大值.

①;②重叠部分的面积始终等于四边形
的
;③
.


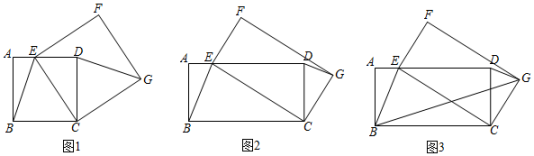
如图①,在正方形中,点E、F分别是
、
上的两点,连接
、
,
, 则
的值为=;
如图③,在四边形中,
. 点E为
上一点,连接
, 过点C作
的垂线交
的延长线于点G,交
的延长线于点F.求证:
;
如图④,点P是上的点,过点P作
, 垂足为O,点O恰好落在对角线
上.求
的值;

如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为.

①如图1,请直接写出AE与DF的数量关系;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;