2023年中考数学探究性试题复习13 平行线的判定与性质-在线组卷

1. (2023七下·上城期中) 【学习新知】射到平面镜上的光线 $\text{[math]}$ 入射光线 $\text{[math]}$ 和反射后的光线 $\text{[math]}$ 反射光线 $\text{[math]}$ 与平面镜所夹的角相等，如图1， $\text{[math]}$ 是平面镜，若入射光线与水平镜面夹角为 $\text{[math]}$ ，反射光线与水平镜面夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．

（1）【初步应用】如图，一束光线 $\text{[math]}$ 射到平面镜 $\text{[math]}$ 上，被 $\text{[math]}$ 反射到平面镜 $\text{[math]}$ 上，又被 $\text{[math]}$ 反射，若被 $\text{[math]}$ 反射出的光线 $\text{[math]}$ 与光线 $\text{[math]}$ 平行，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；
（2）【猜想验证】由（1），请你猜想：当两平面镜 $\text{[math]}$ 、 $\text{[math]}$ 的夹角 $\text{[math]}$ ▲ 时，可以使任何射到平面镜 $\text{[math]}$ 上的光线 $\text{[math]}$ ，经过平面镜 $\text{[math]}$ 、 $\text{[math]}$ 的两次反射后，入射光线 $\text{[math]}$ 与反射光线 $\text{[math]}$ 平行，请说明理由；
（3）【拓展探究】如图 $\text{[math]}$ ，有三块平面镜 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 与镜面 $\text{[math]}$ 的夹角 $\text{[math]}$ ，镜面 $\text{[math]}$ 、 $\text{[math]}$ 的夹角 $\text{[math]}$ ，已知入射光线从镜面 $\text{[math]}$ 开始反射，经过 $\text{[math]}$ 为正整数， $\text{[math]}$ 次反射，当第 $\text{[math]}$ 次反射光线与入射光线 $\text{[math]}$ 平行时，请直接写出 $\text{[math]}$ 的度数． $\text{[math]}$ 可用含有 $\text{[math]}$ 的代数式表示)

答案解析收藏纠错 + 选题

2. (2023七下·深圳期中) 如图

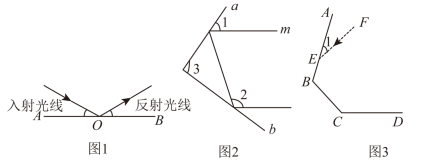
【学习新知】：

射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1， $\text{[math]}$ 是平面镜，若入射光线与水平镜面夹角为 $\text{[math]}$ ，反射光线与水平镜面夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．

（1）【初步应用】：
生活中我们可以运用“激光”和两块相交的平面镜进行测距．如图2当一束“激光” $\text{[math]}$ 射入到平面镜 $\text{[math]}$ 上、被平面镜 $\text{[math]}$ 反射到平面镜 $\text{[math]}$ 上，又被平面镜 $\text{[math]}$ 反射后得到反射光线 $\text{[math]}$ ．回答下列问题：
①当 $\text{[math]}$ ， $\text{[math]}$ （即 $\text{[math]}$ ）时，求 $\text{[math]}$ 的度数．
②当 $\text{[math]}$ 时，任何射入平面镜 $\text{[math]}$ 上的光线 $\text{[math]}$ 经过平面镜 $\text{[math]}$ 和 $\text{[math]}$ 的两次反射后，入射光线 $\text{[math]}$ 与反射光线 $\text{[math]}$ 总是平行的．请你根据所学过的知识及新知说明．
（提示：三角形的内角和等于 $\text{[math]}$ ）
（2）【拓展探究】：
如图3，有三块平面镜 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过三次反射，得到反射光线 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，若要使 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题

3. (2023七下·顺德期中) 将一副三角板中的两个直角顶点 $\text{[math]}$ 叠放在一起，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

（1）操作发现：如图1，当点 $\text{[math]}$ 落在线段 $\text{[math]}$ 上时，写出图中相等的角（写出三对即可）；
（2）问题解决：如图2，若线段 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．
①若 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数；
②当 $\text{[math]}$ 为何值时，使线段 $\text{[math]}$ 最短；
（3）深化拓展：如图3，将三角板 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针转动，直到边 $\text{[math]}$ 与 $\text{[math]}$ 重合即停止，转动的过程中当两块三角板恰有两边平行时，请直接写出 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题

4. (2023七下·南海期中) 几何模型在解题中有着重要作用，例如美味的“猪蹄模型”．

（1）导入：如图1，已知 $\text{[math]}$ ，如果 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ；
（2）发现：如图2，直线 $\text{[math]}$ ，请判断 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由；
（3）运用：如图3，已知 $\text{[math]}$ ， P在射线 $\text{[math]}$ 上运动（点P与点A、B、O三点不重合）， $\text{[math]}$ ， $\text{[math]}$ ，请用含 $\text{[math]}$ 、 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ，并说明理由．

答案解析收藏纠错 + 选题

5. (2023七下·龙岗期中) [阅读探究]如图(a)所示，已知AB∥CD，点E，F分别是AB，CD上的点，点M在AB，CD两平行线之间，∠AEM=45°，∠CFM=25°，求∠EMF的度数．

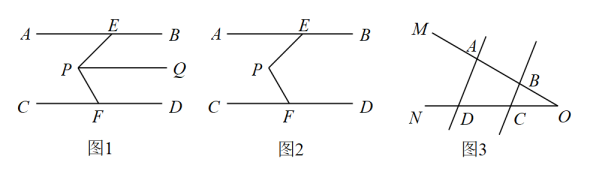
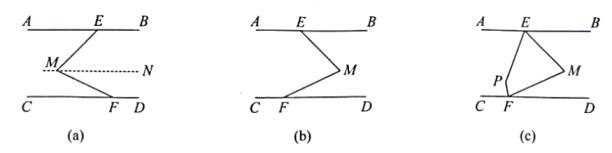
解：如图(a)所示，过点M作MN∥AB．

∵AB∥CD，

∴MN∥CD．

∴∠EMN= CAEM=45°，∠FMN=∠CFM= 25°．

∴∠EMF=∠EMN+∠FMN=45°+25°=70°．

（1）从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠AEM和∠CFM“凑”在一起，得出角之间的关系，使问题得以解决．通过进一步研究，我们可以发现图(a)中∠AEM，∠EMF和∠CFM之间存在一定的数量关系，请直接写出它们之间的数量关系：
（2） [方法运用]如图(b)所示，已知AB∥CD，点E，F分别在直线AB，CD上，点M在AB，CD之间，求∠AEM，∠EMF和∠CFM之间的数量关系．
（3） [应用拓展]如图(C)所示，在图(b)的条件下，分别作LAEM和∠CFM的角平分线EP，FP，交于点P (交点P在AB，CD之间)．若∠EMF=60°，求∠EPF的度数．．

答案解析收藏纠错 + 选题

6. (2023·广东模拟) 【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，若入射光线与水平镜面夹角为 $\text{[math]}$ ，反射光线与水平镜面夹角为 $\text{[math]}$ ，则 $\text{[math]}$ ．

（1）【初步应用】如图2，有两块平面镜 $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过两次反射，得到反射光线 $\text{[math]}$ ，若 $\text{[math]}$ ，证明： $\text{[math]}$ ；
（2）【拓展探究】如图3，有三块平面镜 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，入射光线 $\text{[math]}$ 经过三次反射，得到反射光线 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，若要使 $\text{[math]}$ ，则 $\text{[math]}$ 为多少度？

答案解析收藏纠错 + 选题

7. (2023七下·海曙期中) 如图

（1）问题发现：
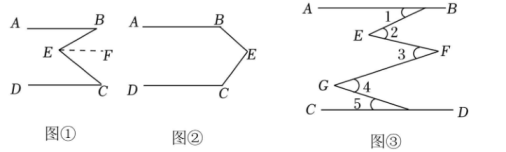
如图①，直线AB∥CD，连接BE，CE，可以发现∠B+∠C=∠BEC．请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC (已知)
∴EF∥DC（）．
∴∠C=∠CEF．（）．
∵EF∥AB，
∴∠B=∠BEF(同理)．
∴∠B+∠C= ▲ (等量代换)．即∠B+∠C=∠BEC．
（2）拓展探究：
如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C+∠BEC=360°．
（3）解决问题：如图③，AB∥DC，E、F、G是AB与CD之间的点，直接写出∠1，∠2，∠3，∠4，∠5之间的数量关系．

答案解析收藏纠错 + 选题

8. (2023七下·永安期中) 如图①，直线 $\text{[math]}$ ，直线EF和直线 $\text{[math]}$ 、 $\text{[math]}$ 分别交于C、D两点，点A、B分别在直线 $\text{[math]}$ 、 $\text{[math]}$ 上，点P在直线EF上，连接PA、PB.

（1）如图①，若点P在线段CD上， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的大小；
（2）猜想：如图①，若点P在线段CD上移动，直接写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系；
（3）探究：如图②，若点P不在线段CD上，则（2）中的数量关系还成立吗？若成立，请说明理由；若不成立，请写出正确的结论并说明理由.

答案解析收藏纠错 + 选题

9. (2023八下·晋安期中) 在一个数学活动中，若身旁没有量角器或者三角尺，又需要作 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的角，可以采用如下的方法：

【操作感知】

第一步：对折矩形纸片 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，得到折痕 $\text{[math]}$ ，把纸片展开.

第二步；再一次折叠纸片，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上，并使折痕经过点 $\text{[math]}$ ，得到折痕 $\text{[math]}$ ，同时得到线段 $\text{[math]}$ （如图1）.

（1）【猜想论证】
写出图1中一个 $\text{[math]}$ 的角：.
（2）若延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，如图 $\text{[math]}$ 所示，试判断 $\text{[math]}$ 的形状，并证明.
（3）【迁移探究】
小华将矩形纸片换正方形纸片，继续探究，过程如下：
将正方形纸片 $\text{[math]}$ 按照 $\text{[math]}$ 操作感知 $\text{[math]}$ 的方式操作，并延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .当点 $\text{[math]}$ 在 $\text{[math]}$ 上时， $\text{[math]}$ ，求正方形的边长.

答案解析收藏纠错 + 选题

10. (2023七下·福州期中) 在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ，动点 $\text{[math]}$ 在射线 $\text{[math]}$ 上从点 $\text{[math]}$ 开始以每秒1个单位长度的速度从左向右运动.

（1）当点 $\text{[math]}$ 运动的时间为2秒时，点 $\text{[math]}$ 的坐标是；
（2）如图1， $\text{[math]}$ ，在点 $\text{[math]}$ 运动的过程中，三角形 $\text{[math]}$ 的面积能等于3吗？若能，请求出点 $\text{[math]}$ 运动的时间；若不能，请说明理由.
（3）如图2， $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，将线段 $\text{[math]}$ 向下平移得到 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上任意一点，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上任意一点， $\text{[math]}$ .点 $\text{[math]}$ 为线段 $\text{[math]}$ 与线段 $\text{[math]}$ 之间一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ .试写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并证明你的结论.

答案解析收藏纠错 + 选题

11. (2023八下·武昌期中) 问题提出：一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质，将有些条件通过平移集中在一起来解决一些几何问题.

如图①，两条长度相等的线段 $\text{[math]}$ 和 $\text{[math]}$ 相交于O点， $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，求线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 满足的数量关系.

分析：考虑将 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 集中到同一个三角形中，以便运用三角形的知识寻求三条线段的数量关系：

如图②，作 $\text{[math]}$ 且 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是平行四边形，从而 $\text{[math]}$ ；

由于 $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ 是等边三角形，故 $\text{[math]}$ ；

通过平行又求得 $\text{[math]}$ .

在 $\text{[math]}$ 中，研究三条线段的大小关系就可以了.

（1）如图②，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的长；
（2）问题解决：如图③，矩形 $\text{[math]}$ 中，E、F分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，满足 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
（3）拓展应用：如图④， $\text{[math]}$ 中， $\text{[math]}$ ， D、E分别在 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ 、 $\text{[math]}$ 交于点O， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

12. (2023七下·新城月考) 问题情境：如图1， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.小明的思路是过点 $\text{[math]}$ 作 $\text{[math]}$ ，通过平行线的性质来求 $\text{[math]}$ .

（1）按照小明的思路，则 $\text{[math]}$ 的度数为；
（2）问题迁移：如图2， $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动，记 $\text{[math]}$ ， $\text{[math]}$ .当点 $\text{[math]}$ 在 $\text{[math]}$ 、 $\text{[math]}$ 两点之间运动时，问 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间有何数量关系？请说明理由；
（3）在（2）的条件下，如果点 $\text{[math]}$ 不在 $\text{[math]}$ 、 $\text{[math]}$ 两点之间运动时（点 $\text{[math]}$ 与点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点不重合），写出 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由.

答案解析收藏纠错 + 选题

13. (2023·泽州模拟) 综合与实践：如图

（1）模型启迪：如图1，在 $\text{[math]}$ 中，D为 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ 并延长至点H，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．由 $\text{[math]}$ ，得 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为，位置关系为．
（2）模型探索：如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， D为 $\text{[math]}$ 边的中点，过点D作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点Q，交 $\text{[math]}$ 边于点K．试判断 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
（3）如图3，在 $\text{[math]}$ 中，D为 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ ， E为 $\text{[math]}$ 边上一点，过点E作 $\text{[math]}$ 于点G，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点F，且 $\text{[math]}$ ．求证： $\text{[math]}$ ．
（4）模型应用：如图4，在（3）的条件下，延长 $\text{[math]}$ 至点N，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点M．若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题

14. (2023·苏州模拟) 【教材再现】

在初中数学教材中有这样一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例.如图1，直线 $\text{[math]}$ ，直线m和直线n分别与直线 $\text{[math]}$ 和直线 $\text{[math]}$ 相交于点A，点B，点F，点D，直线m和直线n相交于点E，则 $\text{[math]}$ ；

【探究发现】

如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D在边 $\text{[math]}$ 上（不与点B，点C重合），连接 $\text{[math]}$ ，点E在边 $\text{[math]}$ 上， $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；
（2）当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的长；
（3）点H在射线AC上，连接EH交线段 $\text{[math]}$ 于点G，当 $\text{[math]}$ ，且 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题

15. (2023·株洲模拟) 阅读下面材料：

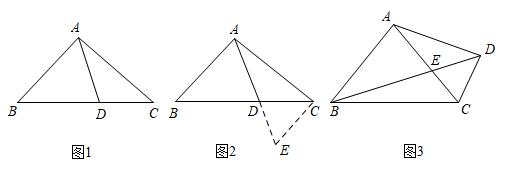
小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD＝75°，∠CAD＝30°，AD＝2，BD＝2DC，求AC的长.

小腾发现，过点C作CE∥AB，交AD的延长线于点E，经过推理和计算能够使问题得到解决，如图2.

（1）请回答：∠ACE的度数为，AC的长为.
（2）参考小腾思考问题的方法，解决问题：
如图3，在四边形ABCD中，∠BAC＝90°，∠CAD＝30°，∠ADC＝75°，AC与BD交于点E，AE＝2，BE＝2ED，求BC的长.

答案解析收藏纠错 + 选题

16. (2023七下·义乌月考) 课题学习：平行线的“等角转化”功能.

（1）阅读理解：如图1，已知点A是 $\text{[math]}$ 外一点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.阅读并补充下面推理过程.
解：过点A作 $\text{[math]}$ ，
$\text{[math]}$ $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ，
$\text{[math]}$ $\text{[math]}$ ，
$\text{[math]}$ $\text{[math]}$ .
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ “凑”在一起，得出角之间的关系，使问题得以解决.
（2）方法运用：如图2，已知 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
（3）深化拓展：已知 $\text{[math]}$ ，点C在点D的右侧， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所在的直线交于点E，点E在直线 $\text{[math]}$ 与 $\text{[math]}$ 之间.
①如图3，点B在点A的左侧，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

②如图4，点B在点A的右侧，且 $\text{[math]}$ ， $\text{[math]}$ .若 $\text{[math]}$ ，求 $\text{[math]}$ 度数.（用含n的代数式表示）