|
销售方式 |
批发 |
零售 |
|
销量(吨/天) |
5 |
2 |
|
利润(元/吨) |
1200 |
2000 |
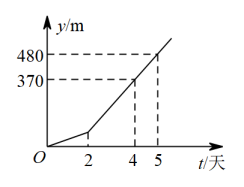
假设该种植户售完22吨苹果,共批发了x吨,所获总利润为y元,
甲商品 | 乙商品 | |
进价(元/件) | 65 | 5 |
售价(元/件) | 90 | 10 |
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品件,甲、乙商品全部销售完后获得利润为
元.
A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格 | 1100 | 1400 |
销售价格 | 今年的销售价格 | 2000 |



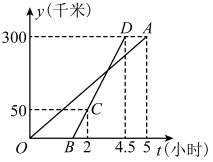





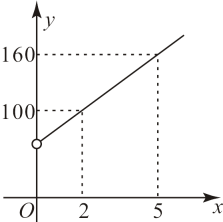
汽车行驶时间 | 0 | 1 | 2 | 3 | |
油箱剩余油量 | 100 | 94 | 88 | 82 |
1 | 2 | 3 | |||
2.4 | 2.8 | 3.2 |

型号 | 载客量(人/辆) | 租金单价(元/辆) |
A | 16 | 900 |
B | 22 | 1200 |
若设租用A型客车x辆,租车总费用为y元.
甲超市:所有商品按原价打8折.
乙超市:一次购物不超过200元的按原价付款,超过200元后超过的部分打7折.
A方案:每分钟元/分钟;
B方案:每月基本服务费元,通话时间600分钟内(含600分钟)免费,超过600分钟的部分按
元/分钟加收通话费;
C方案:每月基本服务费168元,无限畅打,不限时长.