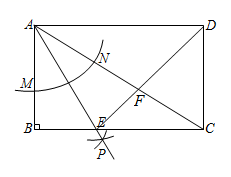


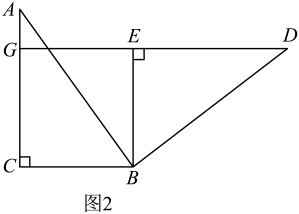
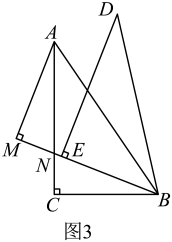
①“善思小组”提出问题:如图3,当时,过点
作
交
的延长线于点
与
交于点
. 试猜想线段
和
的数量关系,并加以证明.请你解答此问题;
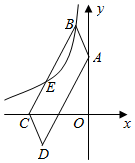
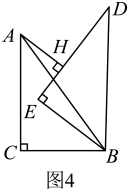
②“智慧小组”提出问题:如图4,当时,过点
作
于点
, 若
, 求
的长.请你思考此问题,直接写出结果.
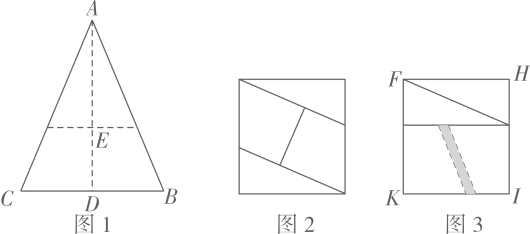
①如图②,当边与
相交于点M、边
与
相交于点N,且矩形
与菱形
重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当时,求S的取值范围(直接写出结果即可).
