2024年北师大版数学七（下）重难点培优训练7 三角形全等的...

更新时间：2024-04-13 浏览次数：60 类型：复习试卷

一、选择题

1. (2023七下·大渡口期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 的平分线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点O， $\text{[math]}$ 交 $\text{[math]}$ 于点D， $\text{[math]}$ 交 $\text{[math]}$ 于点E，若已知 $\text{[math]}$ 周长为20， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
2. (2023七下·宝安期中) 如图所示，在等边三角形 $\text{[math]}$ 内有一点D，连接 $\text{[math]}$ 、 $\text{[math]}$ ，以 $\text{[math]}$ 为边做一个等边三角形 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ，则 $\text{[math]}$ ；④若B、D、C三点共线，则 $\text{[math]}$ ，其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2023八上·淮南期中) 如图，在△AOB和△COD中，OA＝OB ， OC＝OD ， OA＜OC ， ∠AOB＝∠COD＝36°．连接AC ， BD交于点M ，连接OM ．下列结论：
①∠AMB＝36°，②AC＝BD ， ③OM平分∠AOD ， ④MO平分∠AMD ．其中正确的结论个数有（）个．

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
4. (2021七下·肇庆月考) 将一副三角板按如图放置，有下列结论：①若∠2=30°，则AC∥DE；
②∠BAE+∠CAD=180°；③若BC∥AD，则∠2=30°；④若∠CAD=150°，则

∠4=∠C.其中正确的是（）

A . ①②④ B . ①③④ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题
5. (2021七下·巴南期中) 如图，AD∥BC，∠D＝∠ABC，点E是边DC上一点，连接AE交BC的延长线于点H，点F是边AB上一点，使得∠FBE＝∠FEB，作∠FEH的角平分线EG交BH于点G.若∠BEG＝40°，则∠DEH的度数为（　　）

A . 50° B . 75° C . 100° D . 125°

答案解析收藏纠错 + 选题

二、填空题

6. (2023七下·石家庄期中) 已知正方形 $\text{[math]}$ 的边长 $\text{[math]}$ ，将正方形 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在 $\text{[math]}$ 上，展开正方形 $\text{[math]}$ ，折痕为 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．则 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
7. (2023八上·浦东期中) 如图，在△ABC中，AB＝BC ， BE、CF分别是AC、AB边上的高，在BE上取点D ，使BD＝CA ，在射线CF上取点G ，使CG＝BA ，连接AD、AG ，若∠DAE＝38°，∠EBC＝20°，则∠GAB＝°．

答案解析收藏纠错 + 选题
8. (2023八上·花都期中) 如图，已知 $\text{[math]}$ ，从下列条件中选择一个，则可以证明 $\text{[math]}$ 全等于 $\text{[math]}$ ．① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ ，那么这个条件可以是（写出所有符合条件的序号）．

答案解析收藏纠错 + 选题
9. (2020七下·长沙期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，下列说法正确的是.（填写正确的序号）
① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ 平分 $\text{[math]}$ ，④ $\text{[math]}$ 平分 $\text{[math]}$ ，⑤ $\text{[math]}$ ，⑥ $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、综合题

10. (2023八上·津南期中) 数学模型学习与应用：
1. （1）【模型学习】：如图 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ 由 $\text{[math]}$ ，得 $\text{[math]}$ ；又 $\text{[math]}$ ，可以通过推理得到 $\text{[math]}$ ≌ $\text{[math]}$ ，进而得到 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ 我们把这个数学模型称为“一线三等角”模型．
2. （2）【模型应用】：如图 $\text{[math]}$ ， $\text{[math]}$ 为等边三角形， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）【模型变式】：如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
11. (2021七下·乳山期中) 已知： $\text{[math]}$ 是经过 $\text{[math]}$ 的顶点C的一条直线， $\text{[math]}$ ． E、F是直线 $\text{[math]}$ 上两点， $\text{[math]}$ ．
1. （1）若直线 $\text{[math]}$ 经过 $\text{[math]}$ 的内部， $\text{[math]}$ ．
  ①如图1， $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 间的等量关系： ▲ ．
  ②如图2， $\text{[math]}$ 与 $\text{[math]}$ 具有怎样的数量关系，能使①中的结论仍然成立？写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并对结论进行证明；
2. （2）如图3，若直线 $\text{[math]}$ 经过 $\text{[math]}$ 的外部， $\text{[math]}$ ， ①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．
答案解析收藏纠错 + 选题
12. (2020九上·太和期中) 如图1，已知点 $\text{[math]}$ 在同一直线上， $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形， $\text{[math]}$ 交 $\text{[math]}$ 于点F， $\text{[math]}$ 交 $\text{[math]}$ 于点H.
1. （1）求出 $\text{[math]}$ 的度数；
2. （2）请在图1中找出一对全等的三角形，并说明全等的理由；
3. （3）若将 $\text{[math]}$ 绕点C转动如图2所示的位置，其余条件不变，（2）中的结论是否还成立，试说明理由.
答案解析收藏纠错 + 选题
13. (2022·叶县期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为边向右作 $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在 $\text{[math]}$ 边上时，
  ①若 $\text{[math]}$ 时，则 $\text{[math]}$ ▲ $\text{[math]}$ ；
  ②若 $\text{[math]}$ 时，则 $\text{[math]}$ ▲ $\text{[math]}$ ；
  ③观察以上结果，猜想 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
2. （2）当点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上时，请判断 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
答案解析收藏纠错 + 选题
14. (2021七下·历下期中)
1. （1）方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在△ABC中，AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法（如图2），
  ①延长AD到M，使得DM＝AD；
  ②连接BM，通过三角形全等把AB、AC、2AD转化在△ABM中；
  ③利用三角形的三边关系可得AM的取值范围为AB﹣BM＜AM＜AB+BM，从而得到AD的取值范围是多少；
2. （2）请你写出图2中AC与BM的数量关系和位置关系，并加以证明．
3. （3）深入思考：如图3，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠CAF＝90°，请直接利用（2）的结论，试判断线段AD与EF的数量关系，并加以证明．
答案解析收藏纠错 + 选题
15. (2023七下·宣汉期末) 如图1，在△ABC中，∠BAC=90°，AB=AC ，直线MN过点A且MN∥BC ，点D是直线MN上一点，不与点A重合．
1. （1）若点E是图1中线段AB上一点，且DE=DA ，请判断线段DE与DA的位置关系，并说明理由；
2. （2）请在下面的A ， B两题中任选一题解答．
  A：如图2，在（1）的条件下，连接BD ，过点D作DP⊥DB交线段AC于点P ，请判断线段DB与DP的数量关系，并说明理由；
  B：如图3，在图1的基础上，改变点D的位置后，连接BD ，过点D作DP⊥DB交线段CA的延长线于点P ，请判断线段DB与DP的数量关系，并说明理由．
  我选择： ▲ ．
答案解析收藏纠错 + 选题
16. (2023七下·盐田期末) 定理：三角形任意两边之和大于第三边．
1. （1）如图1，线段 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，判断 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，并说明理由；
2. （2）如图2， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上任意一点，在 $\text{[math]}$ ， $\text{[math]}$ 上截取 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ；
3. （3）如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为角平分线 $\text{[math]}$ 上异于端点的一动点，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2023七下·即墨期末) 已知点C为线段 $\text{[math]}$ 上一点，分别以 $\text{[math]}$ 为边在线段AB同侧作 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点F．
1. （1）如图1，可得 $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ ．
2. （2）如图2，若 $\text{[math]}$ ，则 $\text{[math]}$ ．（用含a的式子表示）
3. （3）设 $\text{[math]}$ ，将图2中的 $\text{[math]}$ 绕点C顺时针旋转任意角度（交点F至少在 $\text{[math]}$ 中的一条线段上），如图3．试探究 $\text{[math]}$ 与a的数量关系，并予以说明．
答案解析收藏纠错 + 选题

四、实践探究题

18. (2023七下·宝安期中) 【向题情境】
课外数学兴趣小组活动时，老师提出了如下何题：

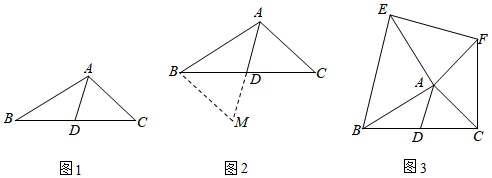
如图①， $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 边上的中线 $\text{[math]}$ 的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长 $\text{[math]}$ 至点E，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，请根据小明的方法思考：
1. （1）由已知和作图能得到 $\text{[math]}$ ，依据是____．
  
  A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$
2. （2）由“三角形的三边关系”可求得 $\text{[math]}$ 的取值范围是．
  解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
3. （3）【初步运用】
  如图②， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 交 $\text{[math]}$ 于E，交 $\text{[math]}$ 于F，且 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
4. （4）【拓展提升】
  如图③，在 $\text{[math]}$ 中，D为 $\text{[math]}$ 的中点， $\text{[math]}$ 分别交 $\text{[math]}$ 于点E，F．求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2023七下·招远期末)
1. （1）如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，若 $\text{[math]}$ 是 $\text{[math]}$ 的平分线，试判断 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系．
  解决此问题可以用如下方法：延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，易证 $\text{[math]}$ ≌ $\text{[math]}$ 得到 $\text{[math]}$ ，从而把 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 转化在一个三角形中即可判断．
  $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系；
2. （2）问题探究：如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，若 $\text{[math]}$ 是 $\text{[math]}$ 的平分线，试探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系，并证明你的结论．
答案解析收藏纠错 + 选题
20. (2023七下·峡江期末) 课外兴趣小组活动时，老师提出了如下问题：
如图①， $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求BC边上的中线AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使 $\text{[math]}$ ，连接BE．由此可证 $\text{[math]}$ ，从而得到 $\text{[math]}$ ，再根据 $\text{[math]}$ 三边关系得出AD取值范围.
1. （1）小明解题过程中证出 $\text{[math]}$ 的依据是____．
  
  A . SAS B . SSS C . AAS D . HL
2. （2）请参考小明的解题思路回答以下问题：
  如图②，AD是 $\text{[math]}$ 的中线，BE交AC于E，交AD于F，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求线段BF的长．
答案解析收藏纠错 + 选题
21. (2023七下·吉林期中) 如图
1. （1）【问题】如图①，在△ABC中，∠A＝74°，DB平分∠ABC，DC平分∠ACB．求∠D的度数，对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
  解：∵∠ABC+∠ACB+∠A＝180°（三角形内角和180° ）．
  ∴∠ABC+∠ACB＝      ▲            （等式性质）．
  ∵∠A＝74° （已知），
  ∴∠ABC+∠ACB＝      ▲            （等量代换）．
  ∵DB平分∠ABC（已知），
  ∴∠DBC＝ $\text{[math]}$ ∠ABC（角平分线的定义）．
  同理，∠DCB＝      ▲            ；
  ∴ $\text{[math]}$ （∠ABC+∠ACB）＝      ▲            （等式性质）．
  ∵∠DBC+∠DCB+∠D＝180°，
  ∴∠D＝180°-（∠DBC+∠DCB）＝      ▲            （等式性质）．
2. （2）【拓展】如图②，在△ABC中，∠A＝β，DB平分∠ABC，DC平分∠ACB．
  则∠D＝（）．
3. （3）【应用】如图③，在△ABC中，DB平分∠ABC，DC平分∠ACB，EB平分∠DBC，EC平分∠DCB．若∠E＝146°，则∠A＝．
答案解析收藏纠错 + 选题
22. (2023七下·西安期末) 【问题背景】
如图，已知 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点G， $\text{[math]}$ 与 $\text{[math]}$ 交于点E．

【问题提出】
1. （1）如图1， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是： $\text{[math]}$ $\text{[math]}$ ；（填“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）
2. （2）【问题探究】如图1，判断 $\text{[math]}$ 和 $\text{[math]}$ 是否相等，并说明理由；
3. （3）如图2，若 $\text{[math]}$ ，当A，O，C三点共线，且 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
23. (2023七下·横山期末) 【问题背景】
直线 $\text{[math]}$ 于点 $\text{[math]}$ （即 $\text{[math]}$ ）， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，一条光线从点 $\text{[math]}$ 射向点 $\text{[math]}$ ，反射后与直线 $\text{[math]}$ 交于点E， $\text{[math]}$ ．
1. （1）【问题再现】
  如图1，试说明线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的数量关系；
2. （2）【问题推广】
  如图2，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ．试说明线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的位置关系．
答案解析收藏纠错 + 选题
24. (2021七下·寿阳期末) 综合与探究：问题情景：如图1所示，已知，在△ABC中，AC＝BA，∠ACB＝90°，AD是△ABC的中线，过点C作CE⊥AD，垂足为M，且交AB于点E．
1. （1）（探究一）小虎通过度量发现∠BCE＝∠CAD，请你帮他说明理由；
2. （2）（探究二）小明在图中添加了一条线段CN，且CN平分∠ACB交AD于点N，如图2所示，即可得CN＝BE，符合题意吗？请说明理由；
3. （3）（探究三）小刚在（2）的基础上，连接DE，如图3所示，又发现了一组全等三角形，你能发现吗？请找出来，并说明理由．
答案解析收藏纠错 + 选题