项目主题:守护生命,“数”说安全.
项目背景:随着社会的发展,安全问题变得日益重要.某校为了提高学生的安全意识,开展以“守护生命,'数'说安全”为主题的项目式学习活动.创新小组通过考察测量、模拟探究和成果迁移等环节,开展地下弯道对通行车辆长度的限制研究.
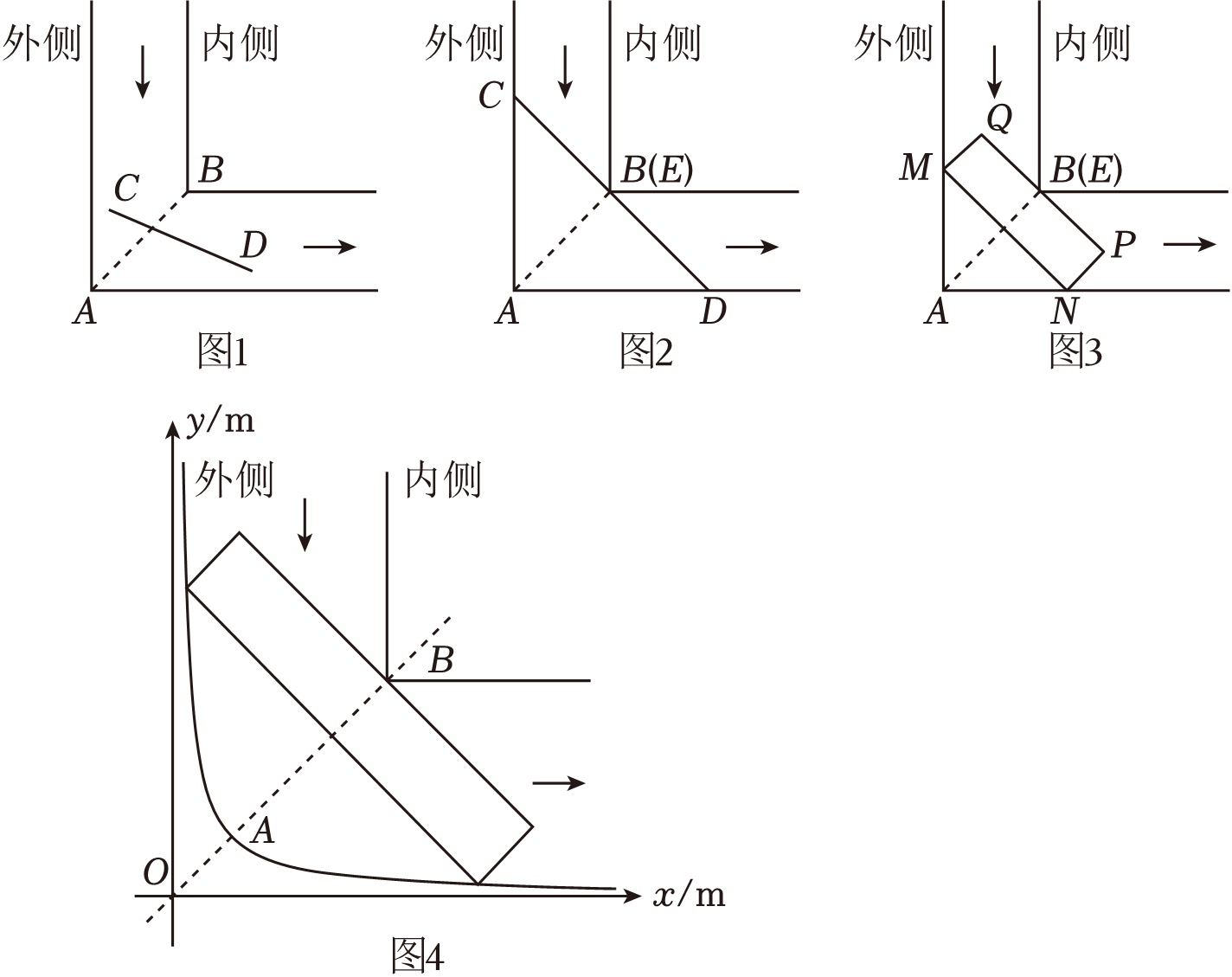
如图1,创新小组所选取弯道的内、外侧均为直角,道路宽均为4m,则AB=m;
如果汽车在行驶中与弯道内、外侧均无接触,则可安全通过.
创新小组用线段模拟汽车通过宽度相同的直角弯道,探究发现:
①当CD<2AB时(如图1),线段CD能通过直角弯道;
②当CD=2AB时,必然存在线段CD的中点E与点B重合的情况,线段CD恰好不能通过直角弯道(如图2).此时,∠ADC的度数是 ;③当CD>2AB时,线段CD不能通过直角弯道.
如图4,某弯道外侧形状可近似看成反比例函数y=(x>0)的图象,其对称轴交图象于点A.弯道内侧的顶点B在射线OA上,两边分别与x轴,y轴平行,OA=2m,AB=4
m.创新小组探究发现通过该弯道的原理与通过直角弯道类似.有一辆长为bm,宽为2m的汽车需要安全通过该弯道,则b的最大整数值为 .(参考数据:
≈1.4,
≈1.7,
≈2.2,
≈2.6)
【项目学习】
配方法是数学中重要的一种思想方法,利用配方法可求一元二次方程的根,也可以求代数式的最值等.所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.其实这种方法还经常被用到代数式的变形中,并结合非负数的意义解决某些问题.
例1:把代数式进行配方.
解:原式.
例2:求代数式的最大值.
解:原式.∵
, ∴
,
∴ , ∴
的最大值为
.
【问题解决】

【项目主题】合理规划,绿色家园
【项目背景】某小区有4栋住宅楼:栋,
栋,
栋,
栋,
处为小区入口. 为方便小区居民传递爱心,物业管理处准备在小区的一条主干道
上增设一个“爱心衣物回收箱”(如图1),现需设计“爱心衣物回收箱”的具体位置,使得它到4栋住宅楼的距离之和最短。某数学兴趣小组成员开展了如下探究活动。

图11-1
任务一 实地测绘
小组成员借助无人机航测技术绘制了小区平面图(如图2),并测量出了某些道路的长度(如表格所示),进一步抽象成几何图形(如图3),其中主干道与
交于点
,
。小组成员又借助电子角度仪测得
.
| 道路 | 长度(米) |
| AE | 40 |
| AB | 30 |
| BC | 30 |
| BF | 18 |
| EF | 32 |
| DE | 25 |
任务二 数学计算
根据图11-3及表格中的相关数据,请完成下列计算:
①根据以上探究,请你在主干道上画出“爱心衣物回收箱”的具体位置(用点
表示),并画出需要增设的小路
;
②“爱心衣物回收箱”到4栋住宅楼的距离之和的最小值为 米。(保留根号)
问题 背景 | 吴兴区某学校决定在校内开辟劳动实践基地,现向全校师生征集实践基地的设计方案.学校项目化学习小组根据学校要求完成了初步设计,请跟随小组成员共同完成以下任务. |
素材一 | 项目化学习小组通过初步研讨,计划利用学校现成的一堵“L”型墙面和栅栏围成长方形的劳动实践基地BFED,其中粗线A-B-C表示墙面,已知AB⊥BC,AB=2米,BC=6米.初步设计方案有两种:如图①,点D在线段BC上;如图②,点D在线段BC的延长线上(包括点C).
|
素材二 | 通过查询学校现有物资信息,学校仓库可提供栅栏的总长度为10米.项目化学习小组决定将这10米栅栏全部用于劳动实践基地中. |
素材三 | 经过市场调查,建造劳动实践基地的人工和材料费合计为25元/平方米. |
根据图1的设计,
若设AF=x,则在①中,DE=;(请用含x的代数式表示)
在②中,长方形BFED的周长为 .
【问题提出】车轮为什么要做成圆形, 这里面有什么数学原理?
【合作探究】

探究 组:如图1,圆形车轮半径为
,其车轮轴心
到地面的距离始终为
.
探究 组:如图2,正方形车轮的轴心为
,若正方形的边长为
,求车轮轴心
最高点与最低点的高度差.
探究 组:如图3, 有一个破损的圆形车轮, 半径为
,破损部分是一个弓形,其所对圆心角为
,其车轮轴心为
,让车轮在地上无滑动地滚动一周,求点
经过的路程.
探究发现:车辆的平稳关键看车轮轴心是否稳定.
【拓展延伸】如图4,分别以正三角形的三个顶点 为圆心,以正三角形的边长为半径作
圆弧,这个曲线图形叫做“莱洛三角形”.
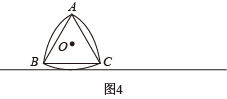

延伸发现:“莱洛三角形”在滚动时始终位于一组平行线之间,因此放在其上的物体也能够保持平衡,但其车轴中心 并不稳定.
|
自制杆秤 |
|||
|
背 景 素 材 |
有言道:“杆秤一头称起人间生计,一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤.如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得: |
|
|
|
设计简易杆秤要求:设定m0=10,M=50,最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米. |
|||
|
问题解决 |
|||
|
任务一 |
确定 |
⑴当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于 ⑵当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于 ⑶根据(1)和(2)所列方程,求出 |
|
|
任务二 |
确定刻线的位置 |
⑷根据任务一,求y关于m的函数解析式. ⑸从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离. |
|


项目反思:同学们对项目学习的整个过程进行反思,并编写了“简易风筝制作说明书”。请你写出一条在项目实施的过程中用到的数学知识
|
项目主题 |
“亚运主题”草坪设计 |
|
项目情境 |
为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草 坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程. |
|
活动任务一 |
请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
|
|
驱动问题一 |
(1)项目小组设计出来的四种方案小路面积的大小关糸? ①直观猜想:我认为 ▲ ;(请用简洁的语言或代数式表达你的猜想) ②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ; ③一般验证:若小路宽为x米,则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ . |
|
活动任务二 |
为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米. |
|
驱动问题二 |
(2)请计算两条小路的宽度是多少? |
|
活动任务三 |
为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边)成面积为100平方米的矩形
|
|
驱动问题三 |
(3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽 ①若30米长的篱笆,请用两种不同的函数表示y关于x的函数关系. ②数学之星小明提出一个问题:若a米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由. |
项目主题:测量旗杆高度

问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
| 方案一 | 方案二 | … | ||
测量工具 | 标杆,皮尺 | 自制直角三角板硬纸板,皮尺 | … | ||
测量示意图 |
说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上. |
说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上. | |||
测量数据 | B,D之间的距离 | 16.8m | B,D之间的距离 | 16.8m | … |
D,F之间的距离 | 1.35m | EF的长度 | 0.50m | … | |
EF的长度 | 2.60m | CE的长度 | 0.75m | … | |
… | … | ||||
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
掷实心球是中考体育考试项目之一,明明发现实心球从出手到落地的过程中,实心球竖直高度与水平距离一直在相应的发生变化.
【提出问题】
实心球竖直高度与水平距离之间有怎样的函数关系?
【分析问题】
明明利用先进的鹰眼系统记录了实心球在空中运动时的水平距离x(单位:米)与竖直高度y(单位:米)的数据如下表:
水平距离 | |||||||
竖直高度 |
根据表中的数据建立如图所示的平面直角坐标系,根据图中点的分布情况,明明发现其图象是二次函数的一部分.

【解决问题】
【提出驱动性问题】如何设计纸盒?
【设计实践任务】选择“素材1”“素材2”设计了“任务1”“任务2”的实践活动.
请你尝试帮助他们解决相关问题.
素材1 | 利用一边长为 |
|
素材2 | 如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖纸盒. |
|
【尝试解决问题】 | ||
任务1 | 初步探究:折一个底面积为 | (1)求剪掉的小正方形的边长为多少? |
任务2 | 折成的无盖纸盒的侧面积是否有最大值? | (2)如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,说明理由. |
如何设计喷泉喷头的升降方案? | ||||||||||||
素材1 | 如图,某景观公园内人工湖里有一个可垂直升降的喷泉,喷出的水柱呈抛物线.记水柱上某一点到喷头的水平距离为x米,到湖面的垂直高度为y米.当喷头位于起始位置时,测量得x与y的四组数据如下:
|
| ||||||||||
素材2 | 公园想设立新的游玩项目,通过升降喷头,使游船能从水柱下方通过,如图,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.4米.已知游船顶棚宽度为2.8米,顶棚到湖面的高度为2米. |
| ||||||||||
问题解决:
结合素材1,求y关于x的表达式.
为使游船按素材2要求顺利通过,求喷头距离湖面高度的最小值.
生活中的数学——自动旋转式洒水喷头如何灌溉草坪 | ||
背景素材 | 数学来源于生活,九4班分四个小组,开展数学项目式实践活动,获取所有数据共享,对草坪喷水管建立数学模型.草坪装有1个自动旋转式洒水喷头,灌溉园林草坪.如图1所示,观察喷头可顺、逆时针往返喷洒. | |
| ||
甲小组在图2中建立合适的直角坐标系,喷水口中心O有一喷水管OA , 从A点向外喷水,喷出的水柱最外层的形状为抛物线.以水平方向为x轴,点O为原点建立平面直角坐标系,点A(喷水口)在y轴上,x轴上的点D为水柱的最外落水点. | 乙小组在甲小组基础上,测量得距洒水喷头水平距离较远若干米的E处,正上方有一树枝叶F , 旋转式喷洒水柱外端刚好碰到树叶F的最低处. | |
丙小组在甲小组基础上,测量得喷水口中心O到水柱的最外落水点D距离为半径,建立⊙O半径为OD的扇形平面图(图3). | ||
问题解决 | ||
任务1 | 获取数据 | 丁小组测量得喷头的高 |
解决问题 | 求出水柱所在抛物线的函数解析式. | |
任务2 | 获取数据 | 丁小组测树叶F距水平地面最低高度 |
解决问题 | 求OE的长. | |
任务3 | 推理计算 | 丁小组观察自动旋转式洒水喷头可顺、逆时针往返喷洒,可平面旋转角度不超过240°,求: ①这个喷头最多可洒水多少平方米? ②在①条件下,此时DD'的长. |
项目主题 | 桥梁模型的承重试验 | ||
活动目标 | 经历项目化学习的全过程,引导学生在实际情境中发现问题,并将其转化为合理的数学问题 | ||
驱动问题 | 当桥梁模型发生不同程度的形变时,水桶下降的高度 | ||
方案设计 | 工具 | 桥梁模型、量角器、卷尺、水桶、水杯、绳子、挂钩等 | |
实物图展示 |
| ||
示意图 | 状态一(空水桶) | 状态二(水桶内加一定量的水) | |
|
| ||
说明:C为 | |||
… | … | ||
请你参与该项目化学习活动,并完成下列问题:
| 项目 | 内容 | ||||
| 课题 | 测量学校附近楼房的高度 | ||||
| 测量示意图 | | 说明:测点D、E与点C、B都在同一水平面上 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| 仰角 | 30.2° | 29.8° | 30° | ||
| 仰角 | 60.1° | 59.9° | 60° | ||
| | 5.1米 | 4.9米 | 5米 | ||
| | 9.8米 | 10.2米 | |||
| … | … | ||||