备考2024年中考数学时事热点抢分练3 决策部署

更新时间：2024-06-03 浏览次数：105 类型：三轮冲刺

一、选择题

1. (2022·肥西模拟) 为贯彻落实党中央、国务院关于推进城乡义务教育一体化发展的部署，教育部会同有关部门近五年来共新建、改扩建校舍188000000平方米，其中数据188000000用科学记数法表示是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九上·交城期末) 按照党中央、国务院决策部署，为了活跃市场主体、助推各地区经济发展，各省市地区抓紧推动稳经济一揽子政策落实落地．江夏区制定了“黄金十条”，坚定企业疫后发展信心，促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元，第二季度的总利润达到500万元，设利润平均月增长率为x，则依题意列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·南宁期中) 为贯彻落实中央关于全面建成小康社会的部署，广大党员干部深入农村积极开展“精准扶贫”工作.某县2018年初统计贫困人口数有729人，经过两年的精准扶贫，2020年初贫困人口还有118人，设每年贫困人口的平均降低率为x，则下面列出的方程中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·明水模拟) 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼．小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图．

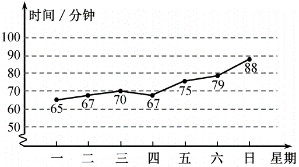
根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）

A . 平均数为70分钟 B . 众数为67分钟 C . 中位数为67分钟 D . 方差为0

答案解析收藏纠错 + 选题
5. 为贯彻落实教育部《关于全面加强新时代大中小学劳动教育的意见》，把劳动教育纳入人才培养全过程，某校组织学生周末赴劳动教育实践基地开展锄地、除草、剪枝、捉鱼、采摘五项实践活动，已知五个项目参与的人数分别是：35，38，39，42，42，则这组数据的众数和中位数分别是（）

A . 38，39 B . 35，38 C . 42，39 D . 42，35

答案解析收藏纠错 + 选题
6. (2024·威信模拟) 在“双减”政策后，学校对某班同学一周七天每天完成课外作业所用的平均时间进行了调查统计，并将统计结果绘制成如图所示的折线统计图，则下列说法错误的是（）

A . 一周完成课外作业所用时间的平均数为50分钟 B . 每天完成课外作业所用时间的中位数是45分钟 C . 每天完成课外作业所用时间的众数是45分钟 D . 每天完成课外作业所用时间的最大值与最小值的差为120分钟

答案解析收藏纠错 + 选题
7. 党的十九大为新时代农业农村改革发展明确了重点，指明了方向.报告中提出了“实施乡村振兴战略”.某地区经过三年的乡村振兴建设，农村的经济收入是振兴前的2倍.为更好地了解该地区农村的经济收入变化情况，统计了该地区乡村振兴建设前后农村的经济收入构成比例，绘制了如图的扇形统计图.

则下列说法中错误的是（）

A . 乡村振兴建设后，养殖收入是振兴前的2倍 B . 乡村振兴建设后，种植收入减少 C . 乡村振兴建设后，其他收入是振兴前的2倍以上 D . 乡村振兴建设后，养殖收入与第三产业收入的总和超过了经济收入的一半

答案解析收藏纠错 + 选题

二、解答题

8. (2023八下·宾阳期末) 参观红色基地，研学红色文化．根据校团委的部署，八年级 $\text{[math]}$ 名师生准备租车到革命历史展览馆参观学习．车站有大小两种车型，每辆大车可坐 $\text{[math]}$ 人，每辆小车可坐 $\text{[math]}$ 人，已知租用大车1辆和小车2辆共需 $\text{[math]}$ 元，租用大车2辆和小车1辆共需 $\text{[math]}$ 元.
1. （1）租大车、小车两种客车每辆各多少元？
2. （2）若学校计划租 $\text{[math]}$ 辆车，其中大车辆有a辆，租车费用w元，能保障所有的八年级师生到革命历史展览馆参观学习，租车费用不超过 $\text{[math]}$ 元，有哪几种租车方案？租车费用最少为多少？
答案解析收藏纠错 + 选题
9. (2023·衢州) 【数据的收集与整理】
根据国家统计局统一部署﹐衢州市统计局对2022年我市人口变动情况进行了抽样调查，抽样比例为5‰.根据抽样结果推算，我市2022年的出生率为5.5‰，死亡率为8‰，人口自然增长率为-2.5‰，常住人口数为 $\text{[math]}$ 人(‰来示千分号).

(数据来源：衢州市统计局)【数据分析】
1. （1）请根据信息推测人口自然增长率与出生率、死亡率的关系.
2. （2）已知本次调查的样本容量为11450，请推算 $\text{[math]}$ 的值.
3. （3）将我市及全国近五年的人口自然增长率情况绘制成如下统计图.根据统计图分析：
  
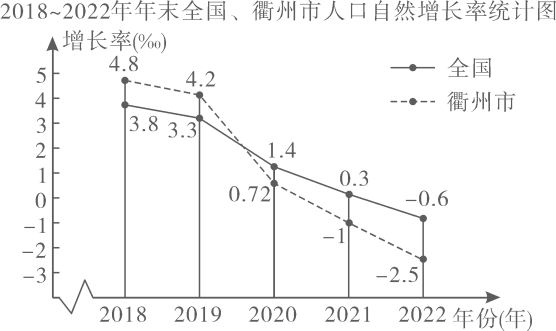
  ①对图中信息作出评判(写出两条).
  
  ②为扭转目前人口自然增长率的趋势，请给出一条合理化建议.
答案解析收藏纠错 + 选题
10. (2021九下·乳山期中) 为落实“精致乳山”工作部署，市政府计划对城区道路进行改造．计划安排甲、乙两个工程队完成，已知甲队的工作效率是乙队工作效率的 $\text{[math]}$ 倍，甲队改造720米的道路比乙队改造同样长的道路少用4天．甲、乙两工程队每天改造道路的长度分别是多少米？

答案解析收藏纠错 + 选题
11. (2024七上·武安期末) 为了进一步贯彻落实“双减”工作，某中学将开展排球、足球兴趣小组活动，体育组王老师购买了排球40个，足球10个，共用了1700元，其中每个排球比每个足球便宜20元．
1. （1）求排球、足球的单价各为多少元；
2. （2）开展活动后，学校决定再次购买这两种球共70个（每种球的单价不变），王老师做完预算后说：“这两种球共需2490元”，请你用所学的知识解释王老师的预算对不对．
答案解析收藏纠错 + 选题
12. (2024·珠海模拟) 为了贯彻全面提高素质教育的要求，了解学生的艺术特长发展情况，学校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中，你最喜欢哪一项活动（每人只限一项）”的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．
请你根据统计图解答下列问题：
1. （1）在这次调查中一共抽查了名学生，其中，喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为，喜欢“戏曲”活动项目的人数是人；
2. （2）若在“①舞蹈、②乐器、③声乐、④戏曲”四个活动项目任选两项设立课外兴趣小组，请用列表或画树状图的方法求恰好选中“①舞蹈、③声乐”这两项活动的概率．
答案解析收藏纠错 + 选题
13. (2024·厚街模拟) 在贯彻落实“五育并举”的工作中，某校开设了五个社团活动：传统国学（A）、科技兴趣（B）、民族体育（C）、艺术鉴赏（D）、劳技实践（E），每个学生每个学期只参加一个社团活动．为了了解本学期学生参加社团活动的情况，学校随机抽取了若干名学生进行调查，并将调查结果绘制成如下两幅尚不完整的统计图．请根据统计图提供的信息，解答下列问题：
1. （1）将条形统计图补充完整；
2. （2）在扇形统计图中，传统国学（A）对应扇形的圆心角度数是；
3. （3）若该校有2700名学生，请估算本学期参加艺术鉴赏（D）活动的学生人数；
4. （4）若小明和小亮可从这五个社团活动中任选一个参加，请直接写出两人恰好选择同一个社团的概率．
答案解析收藏纠错 + 选题
14. (2024·长春汽车经济技术开发模拟) 为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神，汽开区教育局鼓励在校内“学校种植园”开展“活动+劳动教育”课程.某班决定每位学生随机抽取一张卡片来确定自己的种植项目，老师提供3张背面完全相同的卡片，其中正面分别印有白菜、辣椒、茄子图案.把这 3张卡片背面朝上洗匀，小明随机抽取一张，记录后背面朝上放回，重新洗匀后，小华再从中随机抽取一张.请用画树状图(或列表)的方法，求小明和小华抽出的卡片上的图案都是“白菜”的概率.

答案解析收藏纠错 + 选题
15. (2024九上·都江堰期末) 为进一步贯彻《中共中央国务院关于加强消少年体有增强消少年体质的意见》精神，保证学生每天一小时的体育锻炼时间，某校开展了“阳光体育活动”．现决定开设篮球、足球、乒乓球、排球、羽毛球这五项球类活动．为了解同学们对五项球类活动的喜爱情况，学校随机调查了部分学生（每个学生必须选且只能选择这五项活动中的一项），并绘制成如下的统计图．回答下列问题：
1. （1）本次参加调查的学生有 ▲ 人．补全条形统计图；
2. （2）若该校有 $\text{[math]}$ 名学生，那么参加羽毛球活动的学生约有人；
3. （3）九年级一班有甲，乙，丙，丁4名同学参加学校排球队，现从这四名同学中随机抽取2名同学到市上参加比赛，请用树状图或列表法求恰好抽到甲，乙两位同学的概率．
答案解析收藏纠错 + 选题
16. 在“双减”政策实施两个月后，某市“双减办”面向本市城区学生，就“‘双减’前后参加校外学科补习班的情况”(简称“报班”)进行了随机问卷调查，把收集到的数据分两组进行整理，得到如下的统计表和如图所示的统计图.
“双减”前后报班情况统计表(第一组)
0
1
2
3
4及以上
合计
“双减”前
102
48
75
51
24
m
“双减”后
255
15
24
n
0
m
“双减”前后报班情况条形统计图(第二组)
1. （1） m的值为， $\text{[math]}$ 的值为.
2. （2）请你汇总两组数据，求出“双减”后报班数为 3的学生人数所占的百分比.
3. （3） “双减办”汇总数据后，制作了“双减”前后报班情况的折线统计图（图2）.
  ①本次调查中，“双减”前学生报班个数的中位数为， “双减”后学生报班个数的众数为 .
  ②请对该市城区学生“双减”前后报班个数变化情况作出对比分析(用一句话来概括).
答案解析收藏纠错 + 选题
17. (2023九上·丘北月考) 党的二十大报告指出：“全面推进乡村振兴，坚持农业农村优先发展，坚持城乡融合发展，畅通城乡要素流动．”畅通城乡经济循环被摆在突出位置，成为当前和今后阶段全面推进乡村振兴的重要目标，福建某县市通过网络直播带货助力乡村振兴，打响绿色经济发展攻坚战役，某直播间销售某种“特色农产品”，每箱获利40元，每天可卖出30箱，通过市场调查发现：每箱“特色农产品”的售价每降低1元，每天的销售量就增加3箱．
1. （1）若每箱“特色农产品”的售价降低3元，求每天的销售量．
2. （2）为尽快减少库存，决定降价销售，若要使得每天获利1800元，则每箱“特色农产品”的售价需降低多少元？
答案解析收藏纠错 + 选题
18. (2024七上·巴南期末) 为提升乡村休闲旅游产业，推动乡村全面振兴．某地政府计划对辖区内一条长15千米的公路进行维护升级，计划由甲、乙两个工程队联合完成．若甲工程队先单独施工6天，则乙工程队还需单独施工15天可完成该工程．已知甲工程队每天比乙工程队每天少施工0.3千米．
1. （1）求甲、乙两个工程队每天各施工多少千米？
2. （2）已知甲工程队每天的施工费用为8000元，乙工程队每天的施工费用为10000元，若先由甲工程队单独施工若干天，再由甲、乙两个工程队联合施工，则恰好14天完成施工任务，则共需施工费用多少元？
答案解析收藏纠错 + 选题

三、综合题

19. (2024九下·南宁模拟) 今年春北方严重干旱，某社区人畜饮水紧张，每天需从社区外调运饮用水120吨，有关部门紧急部署，从甲、乙两水厂调运饮用水到社区供水点，甲厂每天最多可调出80吨，乙厂每天最多可调出90吨，从两水厂运水到社区供水点的路程和运费如下表：
到社区供水点的路程（千米）
运费（元/吨·千米）
甲厂
20
12
乙厂
14
15
1. （1）若某天调运水的总运费为26700元，则从甲、乙两水厂各调运多少吨饮用水？
2. （2）设从甲厂调运饮用水x吨，总运费为W元，试写出W关于与x的函数关系式，怎样安排调运方案才能使每天的总运费最省？
答案解析收藏纠错 + 选题
20. (2022七下·全椒期末) 为落实“美丽城区”的工作部署，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的 $\text{[math]}$ 倍，甲队改造480米的道路比乙队改造同样长的道路少用4天．
1. （1）甲、乙两工程队每天能改造道路的长度分别是多少米？
2. （2）若甲队工作一天需付费用3万元，乙队工作一天需付费用2.4万元，如需改造的道路全长1200米，改造总费用不超过66万元，至少安排甲队工作多少天？
答案解析收藏纠错 + 选题
21. (2022八上·青秀期中) 为进一步提升摩托车、电动自行车骑乘人员和汽车驾乘人员安全防护水平，公安部交通管理局部署在全国开展“一盔一带”安全守护行动．某商店销售A，B两种头盔，进价和售价如表所示，请根据表格信息下列问题．
名称
A种头盔
B种头盔
进价（元/个）
60
40
售价（元/个）
80
50
1. （1）该商店购进A，B两种头盔共100个，用去4600元钱，求A，B两种头盔各购进了多少个？
2. （2）经过几天销售后商店发现销量较好，于是又用5400元钱购进这两种头盔若干个，要想将这两次购进的头盔售完后所获总利润不低于3000元，则该商店第二次至少应购进A种头盔多少个？
答案解析收藏纠错 + 选题
22. (2024·平阴模拟) 为贯彻落实党的二十大关于深化全民阅读活动的重要部署，教育部印发了《全国青少年学生读书行动实施方案》，于是某中学开展了以“书香润校园，好书伴成长”为主题的系列读书活动．学校为了解学生周末的阅读情况，采用随机抽样的方式获取了若干名学生的周末阅读时间数据，整理后得到下列不完整的图表：
类别
A类
B类
C类
D类
阅读时长t（小时）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
频数
8
m
n
4

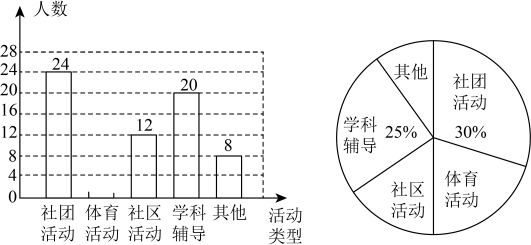
请根据图表中提供的信息，解答下面的问题：
1. （1）此次调查共抽取了名学生， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）扇形统计图中，B类所对应的扇形的圆心角是度；
3. （3）已知在D类的4名学生中有两名男生和两名女生，若从中随机抽取两人参加阅读分享活动，请用列表或画树状图的方法求出恰好抽到一名男生和一名女生的概率．
答案解析收藏纠错 + 选题
23. (2022七下·滨海期末) 某地面对形势异常严峻的新冠疫情，遵从党和国家部署，最大程度保障人民群众的健康，将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区，已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨；用1辆A型车和2辆B型车装满蔬菜一次可运22吨．
1. （1）求一辆A型车和一辆B型车装满蔬菜分别可运多少吨？
2. （2）若一辆A型车的租金是180元，一辆B型车的租金是220元，该地计划租用A型车和B型车共7辆，且租金不超过1400元，问最多可租用几辆B型车？
答案解析收藏纠错 + 选题
24. (2023·锦州) 垃圾分类工作是今年全国住房和城乡建设工作会议部署的重点工作之一．为营造人人参与垃圾分类的良好氛围，某市环保部门开展了“让垃圾分类成为低碳生活新时尚”宣传活动，决定从A ， B ， C三名志愿者中通过抽签的方式确定两名志愿者到社区进行垃圾分类知识宣讲，抽签规则：将三名志愿者的名字分别写在三张完全相同且不透明卡片的正面，把三张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的两张卡片中随机抽取第二张卡片，记下名字．
1. （1）从三张卡片中随机抽取一张，恰好是“B志愿者”的概率是；
2. （2）按照抽签规则，请你用列表法或画树状图法表示出两次抽签所有可能的结果，并求出A ， B两名志愿者同时被抽中的概率．
答案解析收藏纠错 + 选题
25. (2022·德阳) 习近平总书记对实施乡村振兴战略作出重要指示强调：实施乡村振兴战略，是党的十九大作出的重大决策部署，是新时代做好“三农”工作的总抓手.为了发展特色产业，红旗村花费4000元集中采购了A种树苗500株，B种树苗400株，已知B种树苗单价是 A 种树苗单价的1.25倍.
1. （1）求 A 、B两种树苗的单价分别是多少元？
2. （2）红旗村决定再购买同样的树苗100株用于补充栽种，其中A种树苗不多于25株，在单价不变，总费用不超过480元的情况下，共有几种购买方案？哪种方案费用最低？最低费用是多少元？
答案解析收藏纠错 + 选题
26. (2021七下·官渡期末) 为落实“每天锻炼一小时，快乐学习一整天”的要求，官渡区教育体育局部署了校园阳光大课间活动．为了解某校七年级学生每周在校体育锻炼时间，随机抽取了40名学生进行调查．
收集数据
1. （1）下面的抽样方法中，最具代表性和广泛性的是____（填字母）；
  
  A . 抽取40名男生每周在校体育锻炼时间组成样本 B . 抽取40名体育成绩较好的学生每周在校体育锻炼时间组成样本 C . 按学号随机抽取40名学生每周在校体育锻炼时间组成样本
2. （2）整理数据
  依据调查结果绘制了以下不完整的频数分布表：
  时间/小时
  频数
  $\text{[math]}$
  4
  $\text{[math]}$
  10
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  8
  $\text{[math]}$
  12
  合计
  描述数据
  将频数分布表中的数据绘制成不完整的频数分布直方图：
  分析数据
  频数分布直方图中组距为小时；
3. （3）补全频数分布直方图；
4. （4）若该校七年级共有600名学生，估计每周在校参加体育锻炼时间至少有4小时的学生约为多少名？
答案解析收藏纠错 + 选题
27. (2022九上·江城期末) 乌克兰危机发生之后，外交战线按照党中央的部署紧急行动，在战火粉飞中已将5200多名同胞安全从乌克兰撤离，电影《万里归途》正是“外交为民”的真实写照，如表是该影片票房的部分数据，（注：票房是指截止发布日期的所有售票累计收入）
影片《万里归途》的部分统计数据
发布日期
10月8日
10月11日
10月12日
发布次数
第1次
第2次
第3次
票房
10亿元
12.1亿元
1. （1）平均每次累计票房增长的百分率是多少？
2. （2）在（1）的条件下，若票价每张40元，求10月11日卖出多少张电影票
答案解析收藏纠错 + 选题
28. (2021八下·法库期末) 为落实“美丽法库”的工作部署，县政府计划对城区道路进行了改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的 $\text{[math]}$ 倍，甲队改造480米的道路比乙队改造同样长的道路少用4天．
1. （1）求甲、乙两工程队每天能改造道路的长度分别是多少米？
2. （2）若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1200米，改造总费用不超过145万元，至少安排甲队工作多少天？
答案解析收藏纠错 + 选题
29. (2021九下·江北期中) 按照中央精准扶贫的部署，市委、市政府重点扶持贫困户发展特色农业.现某区扶持一贫困户的李子园销售“金脆李”和“黄橙李”两种李子，因为“金脆李”果形奇特、口感佳，售价为30元/斤，“黄橙李”因大面积种植，售价要便宜一些，为20元/斤.
1. （1） 7月上旬，该果园一共售出300斤李子，要使销售额不低于7250元，问最多售出“黄橙李”多少斤？
2. （2）为了提高“金脆李”的知名度，政府对“金脆李”进行广告宣传，7月中旬该果园的总销售重量为1500斤，其中售出“黄橙李”1000斤，7月下旬由于李子大量上市，该果园推出优惠方案，“金脆李”每斤降价a%，“黄橙李”售价保持不变，售后统计“金脆李”销售数量在7月中旬的基础上增加了2a%，“黄橙李”数量在7月中旬的基础上减少了 $\text{[math]}$ a%，若总销售额与7月中旬的总销售额持平，求a的值.
答案解析收藏纠错 + 选题
30. (2023·曲靖模拟) 2022年1月7日，《云南省全民健身实施计划（2021-2025年）》新闻发布会顺利举行．会议上就“十四五”时期深化体育改革，推进新时代全民健身高质量发展作了全面部署和安排．其中，“强化供给，补齐全民健身设施建设短板”是《云南省全民健身实施计划（2021-2025年）》的主要任务之一．春城小区计划购买10台健身器材供小区居民锻炼使用，了解到购买1台B型健身器材比1台A型健身器材贵200元，购买2台A型健身器材和5台B型健身器材共花8000元．
1. （1） A型健身器材和B型健身器材的单价是多少钱？
2. （2）春城小区计划购买B型健身器材的数量不超过A型健身器材的数量的2倍，购买资金不低于10800元，请问共有哪几种购买方案，哪一种方案最省钱．
答案解析收藏纠错 + 选题
31. (2023七下·澄海期末) 为贯彻落实市教育局“课后服务”的文件精神，某校积极开展学生课后服务活动．为更好了解学生对课后服务活动的需求，学校随机抽取了部分学生，进行“我最喜欢的课后服务活动”的调查（每位学生只能选其中一种活动），并将调查结果整理后，形成如下两个不完整的统计图：请根据所给信息解答以下问题：
1. （1）这次参与调查的学生人数为 ▲ 人，请将条形统计图补充完整；
2. （2）扇形统计图中“社团活动”所在扇形的圆心角度数为；
3. （3）若该校共有学生1800人，请估计最喜欢的课后服务活动是“社团活动”的人数约为多少人？
答案解析收藏纠错 + 选题
32. (2023八下·伊川期中) 为贯彻落实《中小学生预防近视眼基本知识与要求》，切实加强学生视力保护工作，某校对全校学生进行了视力检测，并根据统计的八年级某班学生视力情况绘制了如下统计图，其中近视程度在400度以上的有3人．根据扇形统计图回答下列问题：
1. （1）该班近视程度在0∼200的人数所占的百分比是多少?
2. （2）该班共有学生多少名?
3. （3）其中不近视所占扇形圆心角的度数是多少?
答案解析收藏纠错 + 选题
33. (2023八下·邻水期末) 为深入学习贯彻习近平法治思想，推动青少年宪法学习宣传教育走深走实，某校开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动，下表是参加冠亚军决赛的两名选手的各项测试成绩（单位：分）．
选手/项目
在线学习
知识竞赛
演讲比赛
甲
84
96
90
乙
89
99
85
1. （1）若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成组，谁将获得冠军？
2. （2）若将在线学习、知识竞赛与演讲比赛的成绩按2：3：5的比例计算最后成绩，谁将获得冠军？
答案解析收藏纠错 + 选题
34. (2022·莱州模拟) 党中央统一部署指挥全国的抗疫，各级政府统筹安排生产与民生，全民抗疫，同心同德．疫情期间，甲、乙两个蔬菜生产基地向A，B两疫情城市运送蔬菜，以解决民生问题．已知甲、乙两基地共有蔬菜500吨，其中甲基地蔬菜比乙基地少100吨，从甲、乙基地往A，B两城运蔬菜的费用如表．现A城需要蔬菜240吨，B城需要蔬菜260吨．

甲基地
乙基地
A城
20元/吨
15元/吨
B城
25元/吨
30元/吨
1. （1）甲、乙两个蔬菜生产基地各有蔬菜多少吨？
2. （2）设从乙基地运往B城蔬菜x吨，总运费为y元，求y与x之间的函数关系式，并写出自变量x的取值范围；
3. （3）由于开通新的线路，使乙基地运往B城的运费每吨减少 $\text{[math]}$ 元，其余路线运费不变．若总运费的最小值不小于10020元，求a的最大整数解？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2024年中考数学时事热点抢分练3 决策部署

副标题：

*注意事项：

备考2024年中考数学时事热点抢分练3 决策部署

试题分析

总体分析

题量分析

难度分析

知识点分析

	0	1	2	3	4及以上	合计
“双减”前	102	48	75	51	24	m
“双减”后	255	15	24	n	0	m

	到社区供水点的路程（千米）	运费（元/吨·千米）
甲厂	20	12
乙厂	14	15

名称	A种头盔	B种头盔
进价（元/个）	60	40
售价（元/个）	80	50

类别	A类	B类	C类	D类
阅读时长t（小时）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	8	m	n	4

时间/小时	频数
$\text{[math]}$	4
$\text{[math]}$	10
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	8
$\text{[math]}$	12
合计

发布日期	10月8日	10月11日	10月12日
发布次数	第1次	第2次	第3次
票房	10亿元		12.1亿元

选手/项目	在线学习	知识竞赛	演讲比赛
甲	84	96	90
乙	89	99	85

	甲基地	乙基地
A城	20元/吨	15元/吨
B城	25元/吨	30元/吨