浙教版数学九上第3章圆的基本性质一阶单元测试卷

更新时间：2024-09-28 浏览次数：9 类型：单元试卷

一、选择题（本题有10小题，每小题3分，共30分）

1. (2024九上·昆明开学考) 图中是圆心角的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·金华开学考) 一个扇形的半径为6，圆心角为120°，则该扇形的面积是（）

A . 2π B . 4π C . 12π D . 24π

答案解析收藏纠错 + 选题
3. (2024·盐城) 下列四幅图片中的主体事物，在现实运动中属于翻折的是（　　）

A . 工作中的雨刮器 B . 移动中的黑板 C . 折叠中的纸片 D . 骑行中的自行车

答案解析收藏纠错 + 选题
4. (2024·长沙) 如图，在 $\text{[math]}$ 中，弦AB的长为8，圆心O到AB的距离 $\text{[math]}$ ，则 $\text{[math]}$ 的半径长为（）

A . 4 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·江安一诊) 如图，OA，OC是⊙O的半径，点B在⊙O上，若AB∥OC，∠BCO=21°，则∠AOC的度数是（）

A . 42° B . 21° C . 84° D . 60°

答案解析收藏纠错 + 选题
6. (2024·云南模拟) 已知正多边形的一个内角是140°，则这个正多边形的边数是( )

A . 九 B . 八 C . 七 D . 六

答案解析收藏纠错 + 选题
7. (2024九上·广州开学考) 如图，△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A旋转到△AED的位置，使得DC∥AB，则∠BAE等于（）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
8. (2024九上·杭州开学考) 如图，正方形ABCD内接于⊙O，点P在劣弧AB上，连接DP，交AC于点Q．若QP=QO，则 $\text{[math]}$ 的值为（　　）

A . 2 $\text{[math]}$ -1 B . 2 $\text{[math]}$ C . $\text{[math]}$ + $\text{[math]}$ D . $\text{[math]}$ +2

答案解析收藏纠错 + 选题
9. (2024·吉林) 如图，在平面直角坐标系中，点A的坐标为（﹣4，0），点C的坐标为（0，2）．以OA ， OC为边作矩形OABC ．若将矩形OABC绕点O顺时针旋转90°，得到矩形OA^'B^'C^' ，则点B^'的坐标为（）

A . （﹣4，﹣2） B . （﹣4，2） C . （2，4） D . （4，2）

答案解析收藏纠错 + 选题
10. (2023八上·宣化期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上一点，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，将点 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2024九上·金华开学考) 已知四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
12. (2024·长沙) 半径为4，圆心角为 $\text{[math]}$ 的扇形的面积为(结果保留 $\text{[math]}$ ).

答案解析收藏纠错 + 选题
13. (2024·镇江) 如图，四边形ABCD为平行四边形，以点A为圆心，AB长为半径画弧，交BC边于点E ，连接AE ， AB＝1，∠D＝60°，则 $\text{[math]}$ 的长l＝（结果保留π）．

答案解析收藏纠错 + 选题
14. (2024·黑龙江) 如图，△ABC内接于⊙O ， AD是直径，若∠B＝25°，则∠CAD＝°．

答案解析收藏纠错 + 选题
15. (2024八上·长春开学考) 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024九上·惠州期中) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴负半轴交于点A，P是以点 $\text{[math]}$ 为圆心，半径为2的圆上的动点， $\text{[math]}$ 是线段PA的中点，连接OQ，则线段OQ的最小值是.

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题7分，第21题7分，第22题11分，第23题11分，第24题12分，共66分）

17. (2024八下·景德镇期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，过点D作 $\text{[math]}$ ，垂足为点E ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
18. (2024九上·罗湖开学考) △ABC在平面直角坐标系xOy中的位置如图所示．

⑴作△ABC关于点C成中心对称的△A₁B₁C₁ ．

⑵将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂ ．

⑶在x轴上求作一点P ，使PA₁＋PC₂的值最小，并写出点P的坐标（不写解答过程，直接写出结果）

答案解析收藏纠错 + 选题
19. (2024·抚州模拟) 如图，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均在 $\text{[math]}$ 上，请用无刻度的直尺作图．
1. （1）如图1，若点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，试画出 $\text{[math]}$ 的平分线；
2. （2）如图2，若 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ，试画出 $\text{[math]}$ 的平分线．
答案解析收藏纠错 + 选题
20. (2024八下·南山期末) 综合与实践
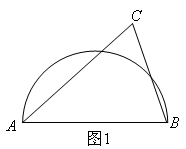
问题情境：“综合与实践”课上，老师提出如下问题：如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转得到 $\text{[math]}$ ，旋转角小于 $\text{[math]}$ ，点 B 的对应点为点D，点 C的对应点为点E， $\text{[math]}$ 交 $\text{[math]}$ 于点O，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点P．

数学思考：（1）试判断 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
深入探究：（2）在以上图形旋转的过程中，老师让同学们提出新的问题．
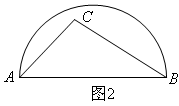
① “乐学小组”提出问题：如图2，当 $\text{[math]}$ 时，则线段 $\text{[math]}$ 的长为．
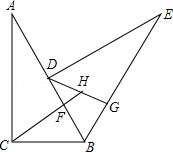
② “善思小组”提出问题：如图3，当 $\text{[math]}$ 时，求线段 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
21. (2024·浙江模拟) 【回顾课本】
浙教版八年级下册数学教材“4.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路，请完成证明过程.
已知：如图1，DE是△ABC的中位线.
求证： $\text{[math]}$
分析：因为E是AC的中点，可以考虑以点E为中心，把△ADE按顺时针方向旋转180°，得到△CFE，这样就只需要证明四边形BCFD是平行四边形.
【探究发现】
如图2，等边△ABC的边长为2，点D，E分别为AB，AC边中点，点F为BC边上任意一点(不与B，C重合)，沿DE，DF剪开分成①，②，③三块后，将②，③分别绕点D，E旋转180°恰好能与①拼成▱DIHG，求▱DIHG周长的最小值.
【拓展作图】
如图3，已知四边形ABCD，现要将其剪成四块，使得剪成的四块能通过适当的摆放拼成一个平行四边形，请在图3中画出剪痕，并对剪痕作适当的说明.

答案解析收藏纠错 + 选题
22. (2024九下·丰城月考) 如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．
1. （1）在图1中，画出△ABC的三条高的交点；
2. （2）在图2中，画出△ABC中AB边上的高．
答案解析收藏纠错 + 选题
23. (2024八下·榕城期中) 如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置.F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H.
1. （1）求证：CF=DG；
2. （2）求出∠FHG的度数.
答案解析收藏纠错 + 选题
24. (2024·广东模拟) 如图，已知 $\text{[math]}$ 是 $\text{[math]}$ 的半径，过 $\text{[math]}$ 上一点D作弦 $\text{[math]}$ 垂直于 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．线段 $\text{[math]}$ 为 $\text{[math]}$ 的直径，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 平分 $\text{[math]}$ ，求 $\text{[math]}$ 的值
答案解析收藏纠错 + 选题