

其中正确的个数是( )
①当m=﹣1时,函数图象的顶点坐标是( ,
);
②当m>0时,函数图象截x轴所得的线段长度大于 ;
③当m<0时,函数在 时,y随x的增大而减小;
④当m≠0时,函数图象经过x轴上一个定点.
其中正确的结论有.(只需填写序号)
【举例】已知点在函数
图象上.点
的“纵横值”为
;函数
图象上所有点的“纵横值”可以表示为
, 当
时,
的最大值为
, 所以函数
的“最优纵横值”为7.
【问题】根据定义,解答下列问题:
②求出函数的“最优纵横值”;
【举例】已知点在函数
图象上.点
的“纵横值”为
;函数
图象上所有点的“纵横值”可以表示为
, 当
时,
的最大值为
, 所以函数
的“最优纵横值”为7.
【问题】根据定义,解答下列问题:
②求出函数的“最优纵横值”;
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为: ,例如17与16的友好数为
.
材料二:对于实数 ,用
表示不超过实数
的最大整数,即满足条件
≤
<
,例如:
,
,
,……
①若 ,
, 则
▲ ;
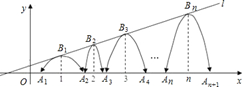
②在图1中,若 ,
, 求
的长.
②函数的图像上的明德点是;
例如:当n=1时,函数y=(x﹣6)2+3关于点P(0,1)的相关函数为y=
(x+6)2﹣1.
①二次函数y=x2关于点P的相关函数为 ;
②点A(2,3)在二次函数y=ax2﹣2ax+a(a≠0)关于点P的相关函数的图象上,求a的值;
如:一次函数y=x-1,关联函数为 , 这个关联函数的转折点是(1,0).
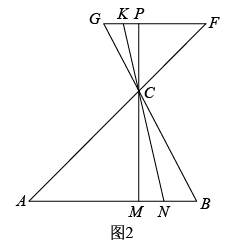
①如图3,连结 , 求弦
的长;
②当时,求
的长.