浙教版数学八年级上册期中模拟测试卷 B

更新时间：2024-10-26 浏览次数：19 类型：期中考试

一、选择题（每题3分，共30分）

1. (2024·眉山) 下列交通标志中，属于轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024·通辽) 将三角尺 $\text{[math]}$ 按如图位置摆放，顶点A落在直线 $\text{[math]}$ 上，顶点B落在直线 $\text{[math]}$ 上，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·雅安) 不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024九下·南岗竞赛) 如图为商场某品牌椅子的侧面图， $\text{[math]}$ ， $\text{[math]}$ 与地面平行， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 70° B . 65° C . 60° D . 50°

答案解析收藏纠错 + 选题
5. 某单位为响应政府号召，需要购买分类垃圾桶6个，市场上有A型和B型两种分类垃圾桶，A型分类垃圾桶500元/个，B型分类垃圾桶550元/个，总费用不超过3100元，则不同的购买方式有（）

A . 2种 B . 3种 C . 4种 D . 5种

答案解析收藏纠错 + 选题
6. (2024·福建) 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案，如图．其中 $\text{[math]}$ 与 $\text{[math]}$ 都是等腰三角形，且它们关于直线 $\text{[math]}$ 对称，点 $\text{[math]}$ 分别是底边 $\text{[math]}$ 的中点， $\text{[math]}$ ．下列推断错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·巴中) “今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问：水深几何？”这是我国数学史上的“葭生池中”问题．即AC＝5，DC＝1，BD＝BA ，则BC＝（）

A . 8 B . 10 C . 12 D . 13

答案解析收藏纠错 + 选题
8. (2024·广州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 的中点，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积为（）

A . 18 B . $\text{[math]}$ C . 9 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·南通) “赵爽弦图”巧妙利用面积关系证明了勾股定理．如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形．设直角三角形的两条直角边长分别为m ， n（m＞n）．若小正方形面积为5，（m+n）²＝21，则大正方形面积为（）

A . 12 B . 13 C . 14 D . 15

答案解析收藏纠错 + 选题
10. (2024·遂宁) 如图1， $\text{[math]}$ 与 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，我们称这样的两个三角形为“伪全等三角形”
如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D ， E在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ，则图中共有“伪全等三角形”( )

A . 1对 B . 2对 C . 3对 D . 4对

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2024·无锡) 命题“若a＞b ，则a﹣3＜b﹣3”是命题．（填“真”或“假”）

答案解析收藏纠错 + 选题
12. (2024·济南) 如图，已知l₁∥l₂ ， △ABC是等腰直角三角形，∠BAC＝90°，顶点A ， B分别在l₁ ， l₂上，当∠1＝70°时，∠2＝°．

答案解析收藏纠错 + 选题
13. (2024·黑龙江) 关于x的不等式组 $\text{[math]}$ 恰有3个整数解，则a的取值范围是．

答案解析收藏纠错 + 选题
14. (2024九下·肇源开学考) 如图， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点O，请添加一个条件，使 $\text{[math]}$ ．（只填一种情况即可）

答案解析收藏纠错 + 选题
15. (2024·绥化) 如图，已知 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 内部一点，点 $\text{[math]}$ 为射线 $\text{[math]}$ 、点 $\text{[math]}$ 为射线 $\text{[math]}$ 上的两个动点，当 $\text{[math]}$ 的周长最小时，则 $\text{[math]}$ 。

答案解析收藏纠错 + 选题
16. (2024·大庆) 如图①，直角三角形的两个锐角分别是40°和50°，其三边上分别有一个正方形．执行下面的操作：由两个小正方形向外分别作锐角为40°和50°的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形．图②是1次操作后的图形．图③是重复上述步骤若干次后得到的图形，人们把它称为“毕达哥拉斯树”．若图①中的直角三角形斜边长为2，则10次操作后图形中所有正方形的面积和为．

答案解析收藏纠错 + 选题

三、解答题（共9题，共72分）

17. (2024·眉山) 解不等式： $\text{[math]}$ ，把它的解集表示在数轴上．

答案解析收藏纠错 + 选题
18. (2024七下·宽城期末) 解不等式组： $\text{[math]}$ ，并写出它的所有整数解．

答案解析收藏纠错 + 选题
19. (2024·常州) 如图，B、E、C、F是直线l上的四点，AC、DE相交于点G ， AB＝DF ， AC＝DE ， BC＝EF ．
1. （1）求证：△GEC是等腰三角形；
2. （2）连接AD ，则AD与l的位置关系是．
答案解析收藏纠错 + 选题
20. (2021八上·淮滨月考) 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）

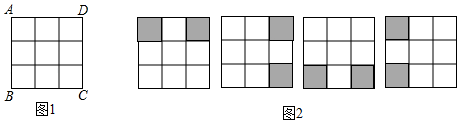
请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）

答案解析收藏纠错 + 选题
21. (2024九下·定日模拟) 为提升学生身体素质，落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神．某校利用课后服务时间，在八年级开展“体育赋能，助力成长”班级篮球赛，共 $\text{[math]}$ 个班级参加．
1. （1）比赛积分规定：每场比赛都要分出胜负，胜一场积 $\text{[math]}$ 分，负一场积 $\text{[math]}$ 分．某班级在 $\text{[math]}$ 场比赛中获得总积分为 $\text{[math]}$ 分，问该班级胜负场数分别是多少？
2. （2）投篮得分规则：在 $\text{[math]}$ 分线外投篮，投中一球可得 $\text{[math]}$ 分，在 $\text{[math]}$ 分线内 $\text{[math]}$ 含 $\text{[math]}$ 分线 $\text{[math]}$ 投篮，投中一球可得 $\text{[math]}$ 分，某班级在其中一场比赛中，共投中 $\text{[math]}$ 个球 $\text{[math]}$ 只有 $\text{[math]}$ 分球和 $\text{[math]}$ 分球 $\text{[math]}$ ，所得总分不少于 $\text{[math]}$ 分，问该班级这场比赛中至少投中了多少个 $\text{[math]}$ 分球？
答案解析收藏纠错 + 选题
22. (2023八上·长沙月考) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且点D在线段 $\text{[math]}$ 上，连 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
23. (2024·新疆维吾尔自治区)
1. （1）【探究】
  已知 $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形.
  ①如图1，当点 $\text{[math]}$ 在BC上时，连接CE.请探究CA，CE和CD之间的数是关系，并说明理由；
  ②如图2，当点D在线段BC的延长线上时，连接CE.请再次探究CA，CE和CD之间的数量关系，并说明理由.
2. （2）【运用】
  如图3，等边三角形ABC中， $\text{[math]}$ ，点 $\text{[math]}$ 在AC上， $\text{[math]}$ .点 $\text{[math]}$ 是直线BC上的动点，连接DE，以DE为边在DE的右侧作等边三角形DEF，连接CF.当 $\text{[math]}$ 为直角三角形时，请直接写出BD的长.
答案解析收藏纠错 + 选题
24. (2024八上·南宁开学考) 【阅读理解】
已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是三个实数， $\text{[math]}$ 表示 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个数的平均数， $\text{[math]}$ 表示 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个数中最小的数．
如 $\text{[math]}$ ， $\text{[math]}$ ；
$\text{[math]}$ ， $\text{[math]}$ ；
解决下列问题：
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值：
3. （3）由（2）可得结论：“若 $\text{[math]}$ ，则______”（填 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系），运用这个结论解决问题：若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
25. (2024九上·新会开学考) 阅读下列材料，并回答问题．
画一个直角三角形，使它的两条直角边分别为5和12，那么我们可以量得直角三角形的斜边长为13，并且 $\text{[math]}$ 事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方．如果直角三角形中，两直角边长分别为a、b，斜边长为c，则 $\text{[math]}$ 这个结论就是著名的勾股定理．
请利用这个结论，完成下面的活动：
1. （1）一个直角三角形的两条直角边分别为6、8，那么这个直角三角形斜边长为．
2. （2）满足勾股定理方程 $\text{[math]}$ 的正整数组 $\text{[math]}$ 叫勾股数组．例如 $\text{[math]}$ 就是一组勾股数组．观察下列几组勾股数
  ①3，4，5； ②5，12，13； ③7，24，25；④9，40，41；
  请你写出有以上规律的第⑤组勾股数：．
3. （3）如图， $\text{[math]}$ 于D， $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题