
 B .
B . 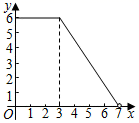 C .
C . 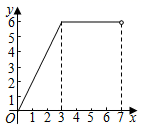 D .
D . 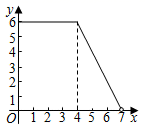


 B .
B .  C .
C .  D .
D . 
| x | …… | -2 | 0 | 3 | 4 | …… |
| y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )


 B .
B .  C .
C .  D .
D . 
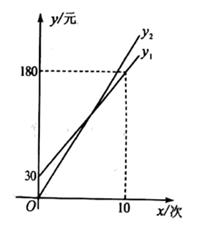
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
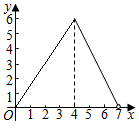
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且
;按照方案二所需费用为
(元) ,且
其函数图象如图所示.
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即
;由周长为m,得
,即
.满足要求的
应是两个函数图象在第象限内交点的坐标.
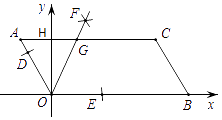
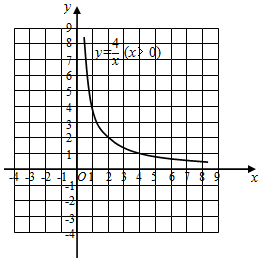
函数 的图象如图所示,而函数
的图象可由直线
平移得到.请在同一直角坐标系中直接画出直线
.
①当直线平移到与函数 的图象有唯一交点
时,周长m的值为;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
若能生产出面积为4的矩形模具,则周长m的取值范围为.
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;
①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.

|
x/cm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y/cm |
9.49 |
7.62 |
5.83 |
|
3.16 |
3.16 |
4.24 |
请你通过计算补全表格;

①三个顶点均在格点上,且其中两个顶点分别是点O,点P;
②三角形的面积等于|k|的值.

|
销售单价x(元) |
… |
25 |
30 |
35 |
40 |
… |
|
每月销售量y(万件) |
… |
50 |
40 |
30 |
20 |
… |
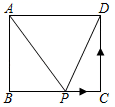
①当 是直角三角形时,求点P的坐标;
②作点B关于点C的对称点 ,则平面内存在直线l,使点M,B,
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
的解析式.(k,b可用含m的式子表示)

①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
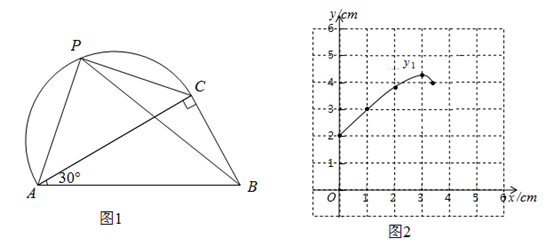
| | 0 | 1 | 2 | 3 | 3.5 |
| | 2 | 3 | 3.8 | 4.4 | 4 |
| | 3.5 | 3.3 | 2.8 | 1.7 | 0 |
如图2,在平面直角坐标系 中,画出了函数
的图象,请在同一坐标系中,描点并画出函数
的图象;