| 体积V | 压强p(kPa) |
| 100 | 60 |
| 90 | 67 |
| 80 | 75 |
| 70 | a |
| 60 | 100 |


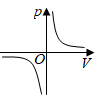 B .
B . 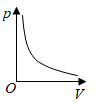 C .
C .  D .
D . 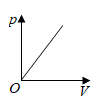
| x/h | 0 | 1 | 2 | 8 | 10 | 12 | 14 | 16 |
| y/m | 14 | 14.5 | 15 | 18 | 14.4 | 12 | 11 | 9 |
满足我们学过的某种函数关系.其中开闸放水有一组数据记录错误,它是( )

 B .
B .  C .
C . 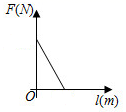 D .
D . 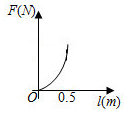



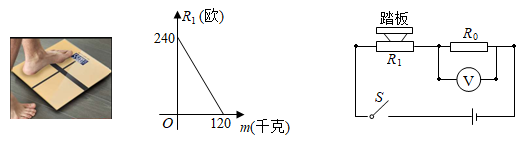
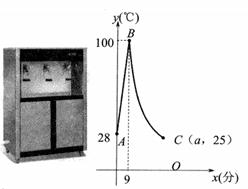
请根据图中信息解答下列问题:

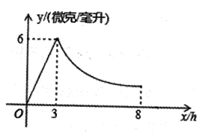

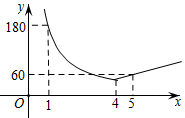
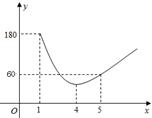
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I= ;
②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.