浙教版备考2022年中考数学一轮复习专题32 圆的动点问题

更新时间：2022-01-12 浏览次数：139 类型：一轮复习

一、单选题

1. (2021八上·平阳期中) 如图，点A是函数y＝ $\text{[math]}$ 的图象上的点，点B，C的坐标分别为B（﹣ $\text{[math]}$ ，﹣ $\text{[math]}$ ），C（ $\text{[math]}$ ， $\text{[math]}$ ）．试利用性质：“函数y＝ $\text{[math]}$ 的图象上任意一点A都满足|AB﹣AC|＝2 $\text{[math]}$ ”求解下面问题：作∠BAC的角平分线AE，过B作AE的垂线交AE于F，已知当点A在函数y＝ $\text{[math]}$ 的图象上运动时，点F总在一条曲线上运动，则这条曲线为（）

A . 直线 B . 抛物线 C . 圆 D . 反比例函数的曲线

答案解析收藏纠错 + 选题
2. (2021九上·鄞州期中) 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为斜边向外作等腰直角三角形△ACD，△BCE，弧AC和弧BC的中点分别是M，N．连接DM，EN，若C在半圆上由点A向B移动的过程中，DM∶EN的值的变化情况是（）

A . 变大 B . 变小 C . 先变大再变小 D . 保持不变

答案解析收藏纠错 + 选题
3. (2021九上·罗庄期中) 如图，在Rt $\text{[math]}$ 中，OA＝OB＝4 $\text{[math]}$ ，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则线段PQ长的最小值为（）

A . 2 $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
4. (2021·西湖模拟) 如图，点A的坐标为（﹣3，2），⊙A的半径为1，P为坐标轴上一动点，PQ切⊙A于点Q ，在所有P点中，使得PQ长最小时，点P的坐标为（　　）

A . （0，2） B . （0，3） C . （﹣2，0） D . （﹣3，0）

答案解析收藏纠错 + 选题
5. (2021·北仑模拟) 如图，点A在半径为6的 $\text{[math]}$ 内， $\text{[math]}$ ，P为 $\text{[math]}$ 上一动点，当 $\text{[math]}$ 取最大值时， $\text{[math]}$ 等于（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·吴兴模拟) 如图，已知在平面直角坐标系 $\text{[math]}$ 中，点M的横坐标为3，以M为圆心，5为半径作 $\text{[math]}$ ，与y轴交于点A和点B，点P是 $\text{[math]}$ 上的一动点，Q是弦 $\text{[math]}$ 上的一个动点，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点E，运动过程中，始终保持 $\text{[math]}$ ，当 $\text{[math]}$ 的结果最大时， $\text{[math]}$ 长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·椒江期中) 如图，半径为1cm的 $\text{[math]}$ 在边长为9πcm，12πcm，15πcm的三角形外沿三边滚动（没有滑动）一周，则圆P所扫过的面积为（）cm²

A . 73π B . 75π C . 76π D . 77π

答案解析收藏纠错 + 选题
8. (2020九上·慈溪期中) 如图，扇形 $\text{[math]}$ 的圆心角的度数为 $\text{[math]}$ ，半径长为4， $\text{[math]}$ 为弧 $\text{[math]}$ 上的动点， $\text{[math]}$ ，垂足分别为 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的外心．当点 $\text{[math]}$ 运动的过程中，点 $\text{[math]}$ 分别在半径上作相应运动，从点 $\text{[math]}$ 离开点 $\text{[math]}$ 时起，到点 $\text{[math]}$ 到达点 $\text{[math]}$ 时止，点 $\text{[math]}$ 运动的路径长（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九上·南沙期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以边的 $\text{[math]}$ 中点 $\text{[math]}$ 为圆心作半圆，使 $\text{[math]}$ 与半圆相切，点 $\text{[math]}$ 分别是边 $\text{[math]}$ 和半圆上的动点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 长的最大值与最小值的和是（）

A . 8 B . 9 C . 10 D . 12

答案解析收藏纠错 + 选题
10. (2020·江干模拟) 已知⊙O的半径为3，A为圆内一定点，AO＝1，P为圆上一动点，以AP为边作等腰△APQ，AP＝PQ，∠APQ＝120°，则OQ的最大值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·芜湖月考) 如图，在矩形ABCD中，AB＝4，BC＝6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为．

答案解析收藏纠错 + 选题
12. (2021九上·东昌府期中) 如图所示，AB，AC与⊙O相切于点B，C，∠A=50°，点P是圆上异于B，C的一动点，则∠BPC的度数是．

答案解析收藏纠错 + 选题
13. (2021九上·龙凤期中) 如图，平面直角坐标系中，分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，以1，3为半径作 $\text{[math]}$ ， $\text{[math]}$ ，M，N分别是 $\text{[math]}$ ， $\text{[math]}$ 上的动点，P为x轴上的动点，则 $\text{[math]}$ 的最小值等于．

答案解析收藏纠错 + 选题
14. (2021·江北模拟) 如图，⊙O的半径为1，弦 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为劣弧 $\text{[math]}$ 上一个动点，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，当点 $\text{[math]}$ 由点 $\text{[math]}$ 运动到点 $\text{[math]}$ 时，点 $\text{[math]}$ 的运动路径长为.

答案解析收藏纠错 + 选题
15. (2021·高港模拟) 如图，AB为⊙O的直径，C为⊙O上一动点，将AC绕点A逆时针旋转120°得AD，若AB＝2，则BD的最大值为.

答案解析收藏纠错 + 选题
16. (2023九上·越城期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是该三角形边上一点，且 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心，1为半径作圆，点 $\text{[math]}$ 是这个圆上的一动点，连接 $\text{[math]}$ ，则线段 $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题

三、综合题

17. (2021九上·龙凤期中) 如图，在半径为5的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．
1. （1）当BC=6时，求线段OD的长；
2. （2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．
答案解析收藏纠错 + 选题
18. (2022九上·温岭期中) 如图，四边形ABCD是⊙O 的内接四边形，对角线AC，BD交于点E，AB=AC.
1. （1）如图1，若BD是⊙O的直径，求证：∠BAC=2∠ACD；
2. （2）如图2，若BD⊥AC，DE =3，CE=4，求BE的长；
3. （3）如图3，若∠ABC+∠DCB=90°，AD=7，BC=24，求AB的长；
4. （4）在（3）的条件下，保持BC不动，使AD在⊙O上滑动，（滑动中AD长度保持不变）直接写出BD+AC的最大值．
答案解析收藏纠错 + 选题
19. (2021九上·长春期中) 如图，在平面直角坐标系中，边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 的四条边与坐标轴平行，顶点A、B分别在第一象限、第二象限，对角线 $\text{[math]}$ 、 $\text{[math]}$ 的交点与坐标原点O重合，当正方形 $\text{[math]}$ 的边上存在点Q，满足 $\text{[math]}$ 时，称点P为正方形 $\text{[math]}$ 的伴随点．
1. （1）点A的坐标为点，B的坐标为，点C的坐标为，点D的坐标为．
2. （2）当正方形 $\text{[math]}$ 的伴随点P的坐标为 $\text{[math]}$ 时，点Q的坐标可以为（写出一个即可）．
3. （3）在点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中，正方形 $\text{[math]}$ 的伴随点是．
4. （4）点P在直线 $\text{[math]}$ 上．若点P为正方形 $\text{[math]}$ 的伴随点，直接写出点P横坐标m的取值范围．
答案解析收藏纠错 + 选题
20. (2021八上·青岛期中) 提出问题：已知平面直角坐标系内，任意一点A ，到另外一个点B之间的距离是度多少？
1. （1）问题解决：
  遇到这种问题，我们可以先从特例入手，最后推理得出结论
  探究一：点A（1，﹣1）到B（﹣1，﹣1）的距离d₁＝，
  
  探究二：点A（2，﹣2）到B（﹣1，﹣1）的距离d₁＝，
  
  一般规律：
  
  如图1，在平面直角坐标系xOy内已知A（x₁ ， y₁）、B（x₂ ， y₂），我们可以表示连接AB ，在构造直角三角形，使两条边交于M ，且∠M＝90°，此时AM＝，BM＝，AB＝．
2. （2）已知互相平行的直线y＝x﹣2与y＝x＋b之间的距离是3 $\text{[math]}$ ，试求b的值．
  拓展延伸：
  
  拓展一：已知点M（﹣1，3）与直线y＝2x上一点N的距离是3，则△OMN的面积是．
  
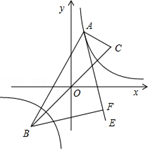
  拓展二：如图2，已知直线y＝ $\text{[math]}$ 分别交x ， y轴于A ， B两点，⊙C是以C（2，2）为圆心，2为半径的圆，P为⊙C上的动点，试求△PAB面积的最大值．
答案解析收藏纠错 + 选题
21. (2021九上·北京月考) 对于平面直角坐标系 $\text{[math]}$ 内任意一点P，过P点作 $\text{[math]}$ 轴于点M， $\text{[math]}$ 轴于点N，连接 $\text{[math]}$ ，则称 $\text{[math]}$ 的长度为点P的垂点距离，记为h．特别地，点P与原点重合时，垂点距离为0．
1. （1）点 $\text{[math]}$ 的垂点距离分别为，，；
2. （2）点P在以 $\text{[math]}$ 为圆心，半径为3的 $\text{[math]}$ 上运动，求出点P的垂点距离h的取值范围；
3. （3）点T为直线 $\text{[math]}$ 位于第二象限内的一点，对于点T的垂点距离h的每个值有且仅有一个点T与之对应，求点T的横坐标t的取值范围．
答案解析收藏纠错 + 选题
22. (2021九上·北京月考) 在平面中，对于 $\text{[math]}$ 以及它的弦 $\text{[math]}$ ，若存在正方形 $\text{[math]}$ ，使点 $\text{[math]}$ 在弦 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，则称正方形 $\text{[math]}$ 是 $\text{[math]}$ 关于弦 $\text{[math]}$ 的一个“联络正方形”
下图中的正方形 $\text{[math]}$ 即为 $\text{[math]}$ 关于弦 $\text{[math]}$ 的一个“联络正方形”

在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径的圆与 $\text{[math]}$ 轴的另一个交点为 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，判断 $\text{[math]}$ 关于弦 $\text{[math]}$ 的“联络正方形”是否存在；
2. （2）当 $\text{[math]}$ 时， $\text{[math]}$ 关于弦 $\text{[math]}$ 的“联络正方形”为 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；
3. （3）当 $\text{[math]}$ 关于弦 $\text{[math]}$ 的“联络正方形”为 $\text{[math]}$ 存在，且点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上时，直接写出此时点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
23. (2021·台州) 如图，BD是半径为3的⊙O的一条弦，BD＝4 $\text{[math]}$ ，点A是⊙O上的一个动点（不与点B，D重合），以A，B，D为顶点作▱ABCD.
1. （1）如图2，若点A是劣弧 $\text{[math]}$ 的中点.
  ①求证：▱ABCD是菱形；
  
  ②求▱ABCD的面积.
2. （2）若点A运动到优弧 $\text{[math]}$ 上，且▱ABCD有一边与⊙O相切.
  ①求AB的长；
  
  ②直接写出▱ABCD对角线所夹锐角的正切值.
答案解析收藏纠错 + 选题
24. (2020九上·镇海期中) 如图，在边长为5的菱形OABC中，sin∠AOC= $\text{[math]}$ ，O为坐标原点，A点在x轴的正半轴上，B，C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周，设运动时间为t（秒）.请解答下列问题：
备用图
1. （1）当CP⊥OA时，求t的值；
2. （2）以点P为圆心，以OP为半径画圆，当⊙P与菱形OABC的一边所在直线相切，且切点不在菱形的边上时，求出t的值.
答案解析收藏纠错 + 选题