”形状，折叠过程按图①、②、③、④的顺序进行（其中阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为
①CA﹣BA＝ ▲ cm；
②若点B以每秒3cm的速度向左移动，同时A、C以每秒1cm、5cm的速度向右移动，设移动时间为t（t＞0）秒，试探究CA﹣AB的值是否会随着t的变化而改变？请说明理由．
①若 ，∠1的度数为a，试求∠3的度数（用含a的代数式表示）：
②若 ，∠3的度数比∠1的度数大20°，试计算∠1的度数.
①求∠PCC的度数；
②若EGC-∠ECG=30°，求∠CPQ的度数。（不能使用“三角形的内角和是180°”直接解题）
①如图1，若∠ABC＝60°，∠ADC＝70°，则∠BED的度数为；
②如图2，设∠ABC＝α，∠ADC＝β，则∠BED的度数为（用含有α，β的式子表示）．
①写出∠AFC，∠BAG的数量关系，并说明理由．
②若∠ABG＝55°，则∠AFC＝ ▲ ．
|
如图，已知△ABC分别用∠1、∠2、∠3表示△ABC的三个内角，证明∠1+∠2+∠3＝180°． 解：延长BC至点E，以点C为顶点，在BE的上侧作∠DCE＝∠2，则CD∥BA（同位角相等，两直线平行） |
①如图二，在△ABC中，∠A＝60°，BP平分∠ABC，CP平分∠ACB，求∠BPC的度数．
②如图三，将△ABC的∠A折叠，使点A落在△ABC外的A1处，折痕为DE．若∠A＝α，∠BDA1＝β，∠CEA1＝γ，则α、β、γ满足的等量关系为 ▲ （用含α、β、γ的代数式表示）．
①如图2，若 、
恰好重合于点О处，MN= cm；
②如图3，若点 落在点
的左侧，且
，MN= cm；
③若 ，MN= cm.（用含n的代数式表示）
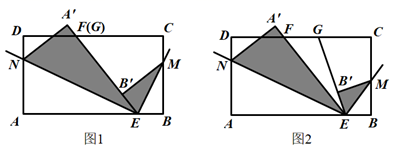
①如图2，当点B'在OA'上时，判断∠AOC与∠BOD的关系，并说明理由；
②如图3，当点B'在∠COA'的内部时，连接OB'，若∠AOC＝44°，∠BOD＝61°，求∠A'OB'的度数．
如图1所示，线段
的长度可表示为：
， 于是他归纳出这样的结论：如果点A表示的数为a，点B表示的数为b，当
时，
（较大数一较小数）.
①如图2所示，计算：
，
；
②把一条数轴在数m对应的点处对折，使表示-20和2020两数的点恰好互相重合，求数m的值；
①如图3所示，点P表示数x，点M表示数
， 点N表示数
， 且
， 求出点P和点N分别表示的数；
②在上述①的条件下，是否存在点Q，使
？若存在，请直接写出点Q所表示的数；若不存在，请说明理由.
小芬在学习过程中，发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示，探索过程如下：如图1所示，线段AB，BC，CD的长度可表示为：AB＝3＝4﹣1，BC＝5＝4﹣（﹣1），CD＝3＝（﹣1）﹣（﹣4），于是他归纳出这样的结论：如果点A表示的数为a，点B表示的数为b，当b＞a时，AB＝b﹣a（较大数﹣较小数）.
①如图2所示，计算：OE＝，EF＝；
②把一条数轴在数m处对折，使表示﹣18和2020两数的点恰好互相重合，则m＝；
①如图3所示，点P表示数x，点M表示数﹣2，点N表示数2x+14，且MN＝4PM，求出点P和点N分别表示的数；
②在上述①的条件下，是否存在点Q，使PQ+QN＝3QM？若存在，请直接写出点Q所表示的数；若不存在，请说明理由.
理由如下：因为 是由
翻折而成，而翻折不改变图形的形状和大小，所以
，所以射线 是∠的角平分线．
①若 ，求
的度数．（写出计算说理过程）
②若 ，求
的度数，从计算中你发现了
的度数有什么规律？（写出计算说理过程）
①对折中心点对应的数为，对折后5对应的点与数对应的点重合；
②若数轴上A、B两点之间的距离为11（A在B的左侧），且A、B两点经折叠后重合，通过计算求A、B两点对应的数分别是多少？
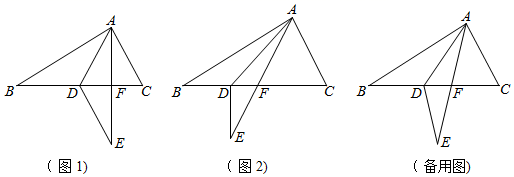
①如（图2），当DE⊥BC时，求x的值.
②是否存在这样的x的值，使得△DEF中有两个角相等.若存在，并求x的值；若不存在，请说明理由.
图3
图4
