
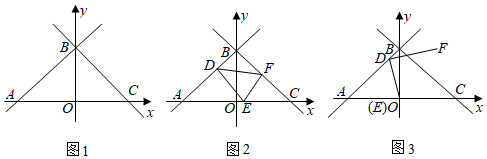
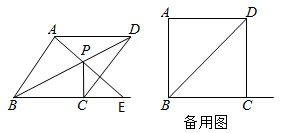
①如图2,当点D的坐标为(﹣2,m),α=45°,且点F恰好落在线段BC上时,求线段AE的长;
②如图3,当点D的坐标为(﹣1,n),α=90°,且点E恰好和原点O重合时,在直线y=3﹣ 上是否存在一点G,使得∠DGF=∠DGO?若存在,直接写出点G的坐标;若不存在,请说明理由.

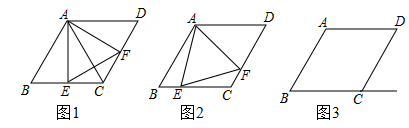
①如图2,求∠GFA的度数;
②如图3,过点G作MH AE,分别交AF,AB,DC于点M,N,H.若AB=3,BF=1,求MH的长.
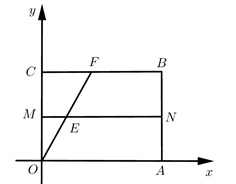
定义:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”﹒例如:如图1,四边形 为菱形,
与
重合,点
在
上,则称菱形
为
的“亲密菱形”.
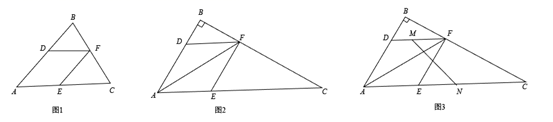
如图2,在 中,
,
平分
,交
于点
,过点
作
,
.
|
n |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
4 |
|||||
|
|
|
2 |
||||
|
|
0 |
0 |
0 |
0 |
0 |
|
①对于 ,
= ,
= ,
,
;
②直线 一定经过的点的坐标为;
求证:1<m<2.


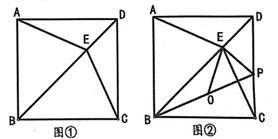


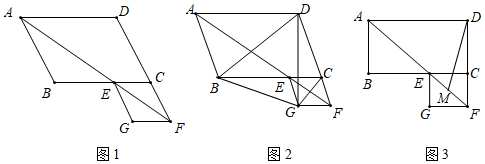
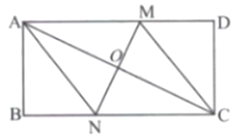
①求证:△DGC≌△BGE;
②求∠BDG的度数;
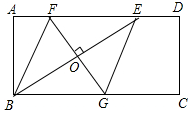
按图1填空:
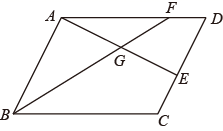
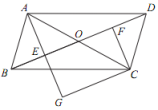
①若▱ABCD的周长是24,OE=2,则四边形ABFE的周长为;
②若▱ABCD的面积是20,则四边形ABFE的面积是.
如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F.若AC= , AD=6,求四边形ABFE的面积.
如图3,在△ABC中,点D是BC的中点,连接AD,若∠BAD=90°,AB=2,AC= , 则△ABC的面积是.
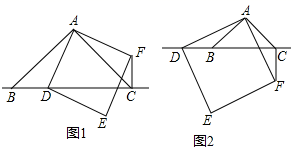
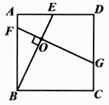
如图1,当点 在线段
上时,
① 与
的位置关系为: ▲ ;
② ,
,
之间的数量关系为: ▲ ;
请将结论直接写在横线上,并给予证明;
如图2,当点 在线段
的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出符合题意结论再给予证明.