2022年中考数学二轮专题复习-与圆有关的位置关系

更新时间：2022-04-18 浏览次数：145 类型：二轮复习

一、单选题

1. (2022九下·萧山开学考) 若⊙O的半径为5cm，点A到圆心O的距离为4cm，则点A与⊙O的位置关系是（）

A . 点A在圆外 B . 点A在圆上 C . 点A在圆内 D . 不能确定

答案解析收藏纠错 + 选题
2. (2021九上·海淀期末) 在△ABC中， $\text{[math]}$ ，点O为AB中点．以点C为圆心，CO长为半径作⊙C，则⊙C 与AB的位置关系是（）

A . 相交 B . 相切 C . 相离 D . 不确定

答案解析收藏纠错 + 选题
3. (2023九上·金东期末) 如图，若 $\text{[math]}$ 的半径为6，圆心O到一条直线的距离为3，则这条直线可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·上城月考) 下列语句中，正确的有（）
①相等的圆心角所对的弧相等；
②等弦对等弧；
③若两个相似多边形的面积比为16：9，那么这两个相似多边形的周长比是4：3；
④已知线段AB＝2，点C是AB的黄全分割点，则 $\text{[math]}$ ；
⑤三角形的外心到三角形的三边距离相等.

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2022九下·重庆开学考) 已知：如图，⊙O是△ABC的外接圆，⊙O的直径为10，过点C作⊙O的切线交AB延长线于点P.BC＝6，则B到CP的距离为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·廉江期末) 如图，⊙O的半径为2，点C是圆上的一个动点，CA⊥x轴，CB⊥y轴，垂足分别为A、B，D是AB的中点，如果点C在圆上运动一周，那么点D运动过的路程长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . π D . 2π

答案解析收藏纠错 + 选题
7. (2021九上·鄞州期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ 于点D，点P为 $\text{[math]}$ 上的点，，以点P为圆心 $\text{[math]}$ 为半径画圆，下列说法错误的是（）

A . 点A在 $\text{[math]}$ 外 B . 点B在 $\text{[math]}$ 外 C . 点C在 $\text{[math]}$ 外 D . 点D在 $\text{[math]}$ 内

答案解析收藏纠错 + 选题
8. (2021九上·香洲期末) 如图，在平面直角坐标系xOy中，点A（0，3），点B（2，1），点C（2，－3）．则经画图操作可知：△ABC的外接圆的圆心坐标是（）

A . （－2，－1） B . （－1，0） C . （－1，－1） D . （0，－1）

答案解析收藏纠错 + 选题
9. (2021九上·和平期末) 如图，两个等圆⊙O₁和⊙O₂相交于A、B两点，且⊙O₁经过⊙O₂的圆心，则∠O₁AB的度数为（　　）

A . 45° B . 30° C . 20° D . 15°

答案解析收藏纠错 + 选题
10. (2021九上·淮南月考) 已知直径分别为6和10的两圆没有公共点，那么这两个圆的圆心距的取值范围是（）

A . d＞2 B . d＞8 C . d＞8或0≤d＜2 D . 2≤d＜8

答案解析收藏纠错 + 选题
11. (2021八上·鼓楼月考) A、B、C表示三个村庄，AB=1000米，BC=600米，AC=800米，为拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（）

A . AB中点 B . BC中点 C . AC中点 D . ∠C的平分线与AB的交点

答案解析收藏纠错 + 选题
12. (2024九下·上海市月考) 已知矩形ABCD的边AB=15，BC=20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是（）.

A . r＞15 B . 15＜r＜20 C . 15＜r＜25 D . 20＜r＜25

答案解析收藏纠错 + 选题
13. (2021九上·罗庄期中) 如图，在Rt $\text{[math]}$ 中，OA＝OB＝4 $\text{[math]}$ ，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则线段PQ长的最小值为（）

A . 2 $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
14. (2021九上·鹿城期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ 是半径为2的 $\text{[math]}$ 上一动点，连结 $\text{[math]}$ ，若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ，则 $\text{[math]}$ 长的最大值为（）

A . 3 B . 305 C . 4 D . 4.5

答案解析收藏纠错 + 选题
15. (2021九上·郯城期中) 如图，在平面直角坐标系中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ的最小值为（）

A . 1 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2022九上·莒南期中) 如图， $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ 是半径为2的 $\text{[math]}$ 上一动点，连结 $\text{[math]}$ ，若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ，则 $\text{[math]}$ 长的最大值为（）

A . 3 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2021九上·鄞州期中) 如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为斜边向外作等腰直角三角形△ACD，△BCE，弧AC和弧BC的中点分别是M，N．连接DM，EN，若C在半圆上由点A向B移动的过程中，DM∶EN的值的变化情况是（）

A . 变大 B . 变小 C . 先变大再变小 D . 保持不变

答案解析收藏纠错 + 选题
18. (2021·路北模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以边 $\text{[math]}$ 的中点 $\text{[math]}$ 为圆心，作半圆与 $\text{[math]}$ 相切，点 $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ 和半圆上的动点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 长的最大值与最小值的和是（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . 9

答案解析收藏纠错 + 选题
19. (2020九上·淮北期末) 如图，A（12，0），B（0，9）分别是平面直解坐标系xOy坐标轴上的点，经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q，则线段PQ长度的最小值是（）

A . $\text{[math]}$ B . 10 C . 7.2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2019九上·如皋期末) 如图，▱ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是边AB上的两点，半径为2的 $\text{[math]}$ 过点A，半径为1的 $\text{[math]}$ 过点 $\text{[math]}$ 、E、F分别是边CD， $\text{[math]}$ 和 $\text{[math]}$ 上的动点 $\text{[math]}$ 则 $\text{[math]}$ 的最小值等于 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . 6 C . $\text{[math]}$ D . 9

答案解析收藏纠错 + 选题

二、填空题

21. (2021九上·中山期末) 已知⊙A的半径为5，圆心A（4，3），坐标原点O与⊙A的位置关系是．

答案解析收藏纠错 + 选题
22. (2021九上·宁波期中) 如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为.

答案解析收藏纠错 + 选题
23. (2021九上·无棣期末) 如图，AB是半圆O的直径，半圆的半径为4，点C，D在半圆上， $\text{[math]}$ ，点P是OC上的一个动点，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
24. (2021九上·章贡期末) 如图，在 $\text{[math]}$ 中，AD为直径，弦 $\text{[math]}$ 于点H，连接OB．已知 $\text{[math]}$ ， $\text{[math]}$ ．动点E从点O出发，在直径AD上沿路线 $\text{[math]}$ 以1cm/s的速度做匀速往返运动，运动时间为 $\text{[math]}$ ．当 $\text{[math]}$ 时， $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
25. (2021九上·陵城期末) 如图，大圆和小圆是等边三角形的外接圆和内切圆，现随机向该图形内掷一枚小针，则针尖落在小圆区域的概率为．

答案解析收藏纠错 + 选题
26. (2021九上·西城期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，点A，B，C的横、纵坐标都为整数，过这三个点作一条圆弧，则此圆弧的圆心坐标为．

答案解析收藏纠错 + 选题
27. (2021九上·潮安期末) 如图， $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形， $\text{[math]}$ ， $\text{[math]}$ ，固定 $\text{[math]}$ ，把 $\text{[math]}$ 绕点C旋转任意角度，连接AD，BE，设AD，BE所在的直线交于点O，则在旋转过程中，始终有 $\text{[math]}$ ，且 $\text{[math]}$ 的大小保持不变，这时点O到直线AB的最大距离为．

答案解析收藏纠错 + 选题
28. (2021九上·龙凤期末) 如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝4，以点C为圆心，3为半径做⊙C，分别交AC，BC于D，E两点，点P是⊙C上一个动点，则 $\text{[math]}$ PA+PB的最小值为．

答案解析收藏纠错 + 选题
29. (2022九上·杭州期中) 如图，△ABC为⊙O的内接等边三角形，BC＝12，点D为 $\text{[math]}$ 上一动点，BE⊥OD于E，当点D由点B沿 $\text{[math]}$ 运动到点C时，线段AE的最大值是．

答案解析收藏纠错 + 选题
30. (2021·温州) 图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的 $\text{[math]}$ 的值为；记图1中小正方形的中心为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，图2中的对应点为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .以大正方形的中心 $\text{[math]}$ 为圆心作圆，则当点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在圆内或圆上时，圆的最小面积为.

答案解析收藏纠错 + 选题

三、解答题

31. (2020九上·江苏月考) 已知⊙O的半径为2，点P到圆心O的距离OP=m，且m使关于x的方程 $\text{[math]}$ 有实数根，求点P与⊙O的位置关系.

答案解析收藏纠错 + 选题
32. 已知：如图，△ABC中， $\text{[math]}$ ， $\text{[math]}$ cm， $\text{[math]}$ cm，CM是中线，以C为圆心，以 $\text{[math]}$ cm长为半径画圆，则点A、B、M与⊙C的关系如何？

答案解析收藏纠错 + 选题
33. 如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r² ，则称点P′是点P关于⊙O的“反演点”．
如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

答案解析收藏纠错 + 选题
34.
如图，在Rt△ABC中，∠ABC=90°，点F为AC中点，⊙O经过点B，F，且与AC交于点D，与AB交于点E，与BC交于点G，连结BF，DE，弧EFG的长度为（1+ $\text{[math]}$ ）π．
（1）求⊙O的半径；
（2）若DE∥BF，且AE=a，DF=2+ $\text{[math]}$ ﹣a，请判断圆心O和直线BF的位置关系，并说明理由．

答案解析收藏纠错 + 选题
35. (2021·光明模拟) 如图，在直角坐标系中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 点，与 $\text{[math]}$ 轴交于 $\text{[math]}$ 点，以 $\text{[math]}$ 为直径作圆 $\text{[math]}$ ，过 $\text{[math]}$ 作圆 $\text{[math]}$ 的切线交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 点的坐标；
2. （2）设点 $\text{[math]}$ 为 $\text{[math]}$ 延长线上一点， $\text{[math]}$ ， $\text{[math]}$ 为线段 $\text{[math]}$ 上的一个动点（异于 $\text{[math]}$ ， $\text{[math]}$ ），过 $\text{[math]}$ 点作 $\text{[math]}$ 轴的平行线交 $\text{[math]}$ 于 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于 $\text{[math]}$ ，试判断 $\text{[math]}$ 的值是否为定值，如果是，则求出这个值；如果不是，请说明理由．
答案解析收藏纠错 + 选题
36. (2019·北京模拟) 对于平面内的⊙C和⊙C外一点Q，给出如下定义：若过点Q的直线与⊙C存在公共点，记为点A，B，设 $\text{[math]}$ ，则称点A（或点B）是⊙C的“K相关依附点”，特别地，当点A和点B重合时，规定AQ=BQ， $\text{[math]}$ （或 $\text{[math]}$ ）．
已知在平面直角坐标系xOy中，Q(-1，0)，C(1，0)，⊙C的半径为r．
1. （1）如图1，当 $\text{[math]}$ 时，
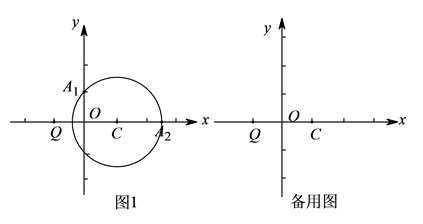
  ①若A₁(0，1)是⊙C的“k相关依附点”，求k的值．
  
  ②A₂(1+ $\text{[math]}$ ，0)是否为⊙C的“2相关依附点”．
2. （2）若⊙C上存在“k相关依附点”点M，
  ①当r=1，直线QM与⊙C相切时，求k的值．
  
  ②当 $\text{[math]}$ 时，求r的取值范围．
3. （3）若存在r的值使得直线 $\text{[math]}$ 与⊙C有公共点，且公共点时⊙C的“ $\text{[math]}$ 相关依附点”，直接写出b的取值范围．
答案解析收藏纠错 + 选题

四、综合题

37. (2021九上·浦口月考) 如图①，在矩形ABCD中，BC＝60cm.动点P以6cm/s的速度在矩形ABCD的边上沿A→D的方向匀速运动，动点Q在矩形ABCD的边上沿A→B→C的方向匀速运动.P、Q两点同时出发，当点P到达终点D时，点Q立即停止运动.设运动的时间为t（s），△PDQ的面积为S（cm²），S与t的函数图象如图②所示.
1. （1） AB＝cm，点Q的运动速度为cm/s；
2. （2）在点P、Q出发的同时，点O也从CD的中点出发，以4cm/s的速度沿CD的垂直平分线向左匀速运动，以点O为圆心的⊙O始终与边AD、BC相切，当点P到达终点D时，运动同时停止.
  ①当点O在QD上时，求t的值；
  ②当PQ与⊙O有公共点时，求t的取值范围.
答案解析收藏纠错 + 选题
38. (2022九上·温岭期中) 如图，四边形ABCD是⊙O 的内接四边形，对角线AC，BD交于点E，AB=AC.
1. （1）如图1，若BD是⊙O的直径，求证：∠BAC=2∠ACD；
2. （2）如图2，若BD⊥AC，DE =3，CE=4，求BE的长；
3. （3）如图3，若∠ABC+∠DCB=90°，AD=7，BC=24，求AB的长；
4. （4）在（3）的条件下，保持BC不动，使AD在⊙O上滑动，（滑动中AD长度保持不变）直接写出BD+AC的最大值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2022年中考数学二轮专题复习-与圆有关的位置关系

副标题：

*注意事项：

2022年中考数学二轮专题复习-与圆有关的位置关系

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析