题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

备考浙教版中考数学题型专项训练方程与不等式解答题专练

更新时间：2022-05-31 浏览次数：82 类型：三轮冲刺

一、综合题

1. (2022八下·仁寿期中) 为了做好学校疫情防控工作，某校从药店购进一批甲、乙两种型号的口罩，已知乙种型号的口罩每袋单价比甲种型号的口罩每袋单价少5元，购买2500元的甲种口罩的数量和购买2000元的乙种口罩的数量相同.
1. （1）求甲、乙两种口罩每袋的售价；
2. （2）根据学校防疫需要，学校拟从该药店购进甲、乙两种型号口罩共800袋，其中乙种型号的数量不超过甲种型号的3倍.问学校应如何购买，才能使得购买口罩所需费用最少？并求出所需的最少费用.
答案解析收藏纠错 + 选题
2. (2022·锦州模拟) 某社区为了创建干净整洁、和谐文明的社区环境，准备购买A，B两种分类垃圾桶，通过市场调研得知：A种垃圾桶每组的单价是B种垃圾桶每组单价的1.5倍，用7200元购买A种垃圾桶的组数比用6000元购买B种垃圾桶少5组．
1. （1）求A，B两种垃圾桶每组单价分别是多少元；
2. （2）该社区计划用不超过12000元的资金购买A，B两种垃圾桶共40组，则最多可以购买A种垃圾桶多少组？
答案解析收藏纠错 + 选题
3. (2022·中山模拟) 有一些相同的房间需要粉刷墙面，一名二级技工粉刷6个房间，5天正好完成；一名一级技工3天粉刷了4个房间还多刷了另外的 $\text{[math]}$ 墙面．每名一级技工比二级技工一天多粉刷 $\text{[math]}$ 墙面．
1. （1）求每个房间需要粉刷的墙面面积；
2. （2）若甲乙两名技工各自需粉刷7个房间的墙面，甲比乙每天少粉刷 $\text{[math]}$ ，乙比甲少用2天完成任务，求甲、乙两名技工每天各粉刷墙面面积．
答案解析收藏纠错 + 选题
4. (2022·坪山模拟) 某超市计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示：

水果单价

甲

乙

进价（元/千克）

$\text{[math]}$

$\text{[math]}$

售价（元/千克）

20

25

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同．
1. （1）求甲、乙两种水果的进价；
2. （2）若该超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，若全部卖完所购进的这两种水果，则超市应如何进货才能获得最大利润，最大利润是多少？
答案解析收藏纠错 + 选题
5. (2022·宝安模拟) 2022年3月12日是第44个植树节，某街道办现计划采购樟树苗和柳树苗共600棵，已知一棵柳树苗比一棵樟树苗贵4元，用2400元所购买的樟树苗与用3200所购买的柳树苗数量相同．
1. （1）请问一棵樟树苗的价格是多少元？
2. （2）若购买樟树苗的数量不超过柳树苗的2倍，怎样采购所花费用最少？最少多少元？
答案解析收藏纠错 + 选题
6. (2022七下·长沙期中) 如图1，在平面直角坐标系中，大正方形OABC的边长为m厘米，小正方形ODEF的边长为n厘米，且 $\text{[math]}$ .
1. （1）求点 $\text{[math]}$ 、点 $\text{[math]}$ 的坐标.
2. （2）起始状态如图1所示，将大正方形固定不动，小正方形以1厘米/秒的速度沿x轴向右平移，如图2.设平移的时间为t秒，在平移过程中两个正方形重叠部分的面积为S平方厘米.
  ①当t=1.5时，S=  ▲  平方厘米；
  
  ②在 $\text{[math]}$ 这段时间内，小正方形的一条对角线扫过的图形的面积为  ▲  平方厘米；
  
  ③在小正方形平移过程中，若S=2，则小正方形平移的时间t为  ▲  秒.
3. （3）将大正方形固定不动，小正方形从图1中起始状态沿x轴向右平移，在平移过程中，连接AD，过D点作DM⊥AD交直线BC于M，∠DAx的角平分线所在直线和∠CMD的角平分线所在直线交于N（不考虑N点与A点重合的情形），求∠ANM的大小并说明理由.
答案解析收藏纠错 + 选题
7. (2022·温州模拟) 已知直线y=2x+m与抛物线y=ax²+ax+b有一个公共点M（1，0），且a＜b.
1. （1）求抛物线顶点Q的坐标（用含a的代数式表示）；
2. （2）说明直线与抛物线有两个交点；
3. （3）直线与抛物线的另一个交点记为N.
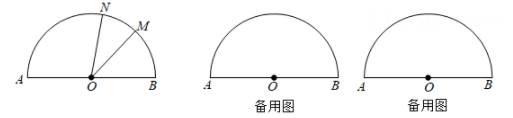
  （Ⅰ）若-1≤a≤ $\text{[math]}$ ，求线段MN长度的取值范围；
  
  （Ⅱ）求△QMN面积的最小值.
答案解析收藏纠错 + 选题
8. (2022七下·西湖月考) 今年疫情期间某物流公司计划用两种车型运输救灾物资，已知：用2辆A型车和1辆B型车装满物资一次可运10吨；用1辆A型车和2辆B型车一次可运11吨.某物流公司现有31吨货物资，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满.
1. （1） 1辆A型车和1辆B型车都装满物资一次可分别运多少吨?
2. （2）请你帮该物流公司设计租车方案；
3. （3）若A型车每辆需租金每次100元，B型车租金每次120元，请选出最省钱的租车方案，并求出最少租车费.
答案解析收藏纠错 + 选题
9. (2022八下·拱墅月考) 如图，在长方形 $\text{[math]}$ 中，边 $\text{[math]}$ 、 $\text{[math]}$ 的长 $\text{[math]}$ 是方程 $\text{[math]}$ 的两个根.点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 个单位的速度沿 $\text{[math]}$ 边 $\text{[math]}$ 的方向运动，运动时间为 $\text{[math]}$ 秒 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 的长；
2. （2）当点 $\text{[math]}$ 运动到边 $\text{[math]}$ 上时，试求出使 $\text{[math]}$ 长为 $\text{[math]}$ 时运动时间 $\text{[math]}$ 的值；
3. （3）当点 $\text{[math]}$ 运动到边 $\text{[math]}$ 上时，是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 是等腰三角形？若存在，请求出运动时间 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
10. (2022七下·华安月考) 在一次地震中，某村受地震影响严重，已经成为一片废墟.为重建家园，政府准备修建在地震中受损的一条公路，若由甲工程队单独修需3个月完成，每月耗资12万元；若由乙工程队单独修建需6个月完成，每月耗资5万元.
1. （1）请问若由甲、乙两工程队合作修建需几个月完成？共耗资多少万元？
2. （2）若由甲、乙两工程队先合作，剩下的由乙队来完成，且恰好历时4个月完成修建任务，求这样安排共耗资多少万元？（时间按整月计算）
答案解析收藏纠错 + 选题

11. (2022·温州模拟) 某产家在甲、乙工厂生产同一商品，并将其分几天运往A地240吨，B地260吨，表1是两个工厂的商品记录，表2为该商品的运费标准（m，n为常数）.

表1

时间	甲工厂商品记录	乙工厂商品记录	甲、乙两工厂总运费
第1天	生产商品200吨	生产商品300吨
第2天	运往A地30吨	运往A地10吨，运往B地20吨	1230元
第3天	运往B地20吨	运往B地40吨	1460元

甲乙两厂往A，B地运输该商品的运费标准（单位：元/吨）

表2

目的地

工厂

A

B

甲

20

25

乙

m

n

（1）求m，n的值.
（2）若运费标准不变，要使剩余商品按要求运往A，B两地，且总运费最少，请给出剩余商品的运输方案.
（3）若从第4天开始，运输公司将甲工厂往B地的运费提高a元/吨，乙工厂往B地的运费降低a元/吨，其中a为正整数，若可用不超过7150元的费用按要求完成剩余商品的运输，求a的最小值.

答案解析收藏纠错 + 选题

12. (2022·乐清模拟) 学校趣味运动会组织跳绳项目，购买跳绳经费最多95元.某商店有A，B，C三个型号的跳绳，跳绳价格如下表所示，已知B型长度是A型两倍，C型长度是A型三倍（同个型号跳绳长度一样），用80米绳子制作A型的数量比120米绳子制作B型的数量还多5根.

规格

A型

B型

C型

单价（元/条）

4

6

9
1. （1）求三种型号跳绳的长度.
2. （2）若购买三种跳绳经费刚好用完，其中A型和B型跳绳条数一样多，且所有跳绳总长度为120米，求购买A型跳绳的数量.
3. （3）若购买的跳绳长度总长度不少于100米，则A型跳绳最多买几条？
答案解析收藏纠错 + 选题
13. 某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过12吨（含12吨）时，按每吨1元收费；每月超过12吨时，超过部分每吨按市场调节价收费，小黄家1月份用水24吨，交水费42元.
1. （1）求每吨水的市场调节价是多少元；
2. （2）设每月用水量为x（x＞12）吨，应交水费为y元，写出y与x之间的关系式；
3. （3）小张家3月份用水28吨，他家应交水费多少元？
答案解析收藏纠错 + 选题
14. (2022八下·开福月考) 在平面直角坐标系中，O是坐标原点，矩形ABCO的顶点A、C分别在x轴、y轴上，已知B点坐标为 $\text{[math]}$ ，且a，b满足 $\text{[math]}$ ，若点M沿线段CB从C向B以每秒2cm的速度运动至B，同时动点N沿线段AO从A向O以同样的速度运动，当其中一个点停止时，另一个也停止运动，设运动时间为t秒，连接OM、BN；
1. （1）如图1，当t为何值时，四边形OMBN是菱形？
2. （2）如图2，将矩形OABC沿着AP折叠，点O的对应点 $\text{[math]}$ 恰好落在BC边上，连接 $\text{[math]}$ ，求直线 $\text{[math]}$ 的函数解析式；
3. （3）如图3，点P是对角线OB上一动点，点Q是OA上一动点，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
15. (2022七下·南阳开学考) 阅读下列解方程组的方法，然后解答问题：
解方程组 $\text{[math]}$ 时，小明发现如果用常规的代入消元法、加减消元法来解，计算量大，且易出现运算错误，他采用下面的解法则比较简单：
②-①得： $\text{[math]}$ ，即 $\text{[math]}$ .③
$\text{[math]}$ 得： $\text{[math]}$ .④
①-④得： $\text{[math]}$ ，代入③得 $\text{[math]}$ .
所以这个方程组的解是 $\text{[math]}$ .
1. （1）请你运用小明的方法解方程组 $\text{[math]}$ .
2. （2）规律探究：猜想关于 $\text{[math]}$ 、 $\text{[math]}$ 的方程组 $\text{[math]}$ 的解是.
答案解析收藏纠错 + 选题
16. (2022九下·重庆开学考) 如图，已知抛物线y=ax²+bx-4与x轴交于A，B两点，与y轴交于点C，且点A的坐标为（-2，0），直线BC的解析式为y= $\text{[math]}$ x-4.
1. （1）求抛物线的解析式；
2. （2）如图1，过点A作AD∥BC交抛物线于点D（异于点A），P是直线BC下方抛物线上一点，过点P作PQ∥y轴，交AD于点Q，过点Q作QR⊥BC于点R，连接PR.求△PQR面积的最大值及此时点P的坐标；
3. （3）如图2，点C关于x轴的对称点为点C′，将抛物线沿射线C′A的方向平移2 $\text{[math]}$ 个单位长度得到新的抛物线y′，新抛物线y′与原抛物线交于点M，原抛物线的对称轴上有一动点N，平面直角坐标系内是否存在一点K，使得以D，M，N，K为顶点的四边形是矩形？若存在，请直接写出点K的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
17. (2022六下·哈尔滨开学考) 中学原计划在一个直径为20米的圆形场地内修建圆形花坛（花坛指的是图中实线部分），为使花坛修得更加美观、有特色，决定向全校征集方案，在众多方案中最后选出三种方案：
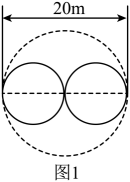
方案A：如图1所示，先画一条直径，再分别以两条半径为直径修两个圆形花坛；

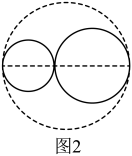
方案B：如图2所示，先画一条直径，然后在直径上取一点，把直径分成2：3的两部分，再以这两条线段为直径修两个圆形花坛；

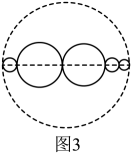
方案C：如图3所示，先画一条直径，然后在直径上任意取四点，把直径分成5条线段，再分别以这5条线段为直径修5个圆形花坛．
1. （1）如果按照方案A修，修的花坛的周长是．
2. （2）如果按照方案B修，与方案A比，省材料吗？为什么？
3. （3）如果按照方案C修，学校要求在8小时内完成，甲工人承包了此项工程，他做了4小时后，发现不能完成任务，就请乙来帮忙，乙的效率是甲的 $\text{[math]}$ ，乙加入后，甲的效率也提高了 $\text{[math]}$ ，结果正好按时完成任务，若修1米花坛可得到10元钱，修完花坛后，甲可以得到多少钱？（ $\text{[math]}$ 取3）
答案解析收藏纠错 + 选题
18. (2022八下·泾阳月考) 临近2022年春节，西安疫情形势较为严峻，对确诊病例所在地区实行区域管控，严格履行疫情防控措施为防范疫情，某校欲购置规格分别为300mL和500mL的甲、乙两种消毒液若干瓶，已知购买2瓶甲种和1瓶乙种消毒液需要61元，购买3瓶甲种和4瓶乙种消毒液需要154元。
1. （1）求甲，乙两种消毒液的单价；
2. （2）为节约成本，该校购买散装消毒液进行分装，现需将11.2L的消毒液全部装人最大容量分别为300mL和500mL的两种空瓶中（每瓶均装满），若分装时平均每瓶需损耗20mL，请问如何分能使总损耗最小？求出此时需要的两种空瓶的数量．
答案解析收藏纠错 + 选题
19. (2022九下·泉州开学考) 为了响应“践行核心价值观，传递青春正能量”的号召，小颖决定走入社区号召大家参加“传递正能量志愿服务者”.假定从一个人开始号召，每一个人每周能够号召相同的m个人参加，被号召参加的人下一周会继续号召，两周后，将有121人被号召成为“传递正能量志愿服务者”.
1. （1）求出m的值；
2. （2）经过计算后，小颖、小红、小丽三人开始发起号召，但刚刚开始，他们就发现了问题，实际号召过程中，不是每一次号召都可以成功，而他们三人的成功率也各不相同，已知小红的成功率比小颖的两倍少10%，第一周后小丽比小颖多号召2人，三人一共号召17人，其中小颖号召了n人.请分别求出他们三人号召的成功率.
答案解析收藏纠错 + 选题
20. (2022八下·浙江期末) 模具厂计划生产面积为4，周长为m的矩形模具.对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：
1. （1）建立函数模型
  设矩形相邻两边的长分别为x，y，由矩形的面积为4，得 $\text{[math]}$ ，即 $\text{[math]}$ ；由周长为 $\text{[math]}$ ，得 $\text{[math]}$ ，即 $\text{[math]}$ $\text{[math]}$ .满足要求的 $\text{[math]}$ 应是两个函数图象在第象限内交点的坐标.
2. （2）画出函数图象
  函数 $\text{[math]}$ 的图象如图所示，而函数 $\text{[math]}$ 的图象可由直线 $\text{[math]}$ 平移得到.请在同一直角坐标系中直接画出直线 $\text{[math]}$ .
3. （3）平移直线 $\text{[math]}$ ，观察函数图象
  ①当直线平移到与函数 $\text{[math]}$ 的图象有唯一交点 $\text{[math]}$ 时，周长 $\text{[math]}$ 的值为▲ ；
  
  ②在直线平移过程中，交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
4. （4）得出结论
  若能生产出面积为4的矩形模具，则周长m的取值范围为.
答案解析收藏纠错 + 选题
21. 如图， $\text{[math]}$ 是边长为 $\text{[math]}$ 的等边三角形，动点P，Q同时从A，B两点出发，分别沿AB，BC方向匀速移动，它们的速度都是 $\text{[math]}$ ，当点 $\text{[math]}$ 到达点 $\text{[math]}$ 时，P，Q两点停止运动，设点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ ，解答下列问题：
1. （1）求 $\text{[math]}$ 的面积.
2. （2）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 是直角三角形？
3. （3）是否存在某一时刻 $\text{[math]}$ ，使四边形APQC的面积是 $\text{[math]}$ 面积的 $\text{[math]}$ ？如果存在，求出 $\text{[math]}$ 的值；如果不存在，请说明理由.
答案解析收藏纠错 + 选题
22. (2022七上·遵义期末) 已知数轴上两点A，B对应的数分别是 $\text{[math]}$ ，4，P、M、N为数轴上的三个动点，点M从B点出发速度为每秒2个单位，点N从A点出发速度为M点的2倍，点P从原点出发速度为每秒1个单位.
1. （1）线段 $\text{[math]}$ 之间的距离为个单位长度.
2. （2）若点M向左运动，同时点N向右运动，求多长时间点M与点N相遇？
3. （3）若点M、N、P同时都向右运动，求多长时间点P到点M，N的距离相等？
答案解析收藏纠错 + 选题
23. (2022七上·石阡期末) 如图1，已知点C在线段AB上，线段AC＝10厘米，BC＝6厘米，点M，N分别是AC，BC的中点.
1. （1）求线段MN的长度.
2. （2）根据第（1）题的计算过程和结果，设AC＝a，BC＝b，其他条件不变，求MN的长度.
3. （3）动点P、Q分别从A、B同时出发，点P以2cm/s的速度沿AB向右运动，终点为B，点Q以1cm/s的速度沿AB向左运动，终点为A，当一个点到达终点，另一个点也随之停止运动.设点P的运动时间为t（s）.当C、P、Q三点中，有一点恰好是以另外两点为端点的线段的中点时，直接写出时间t.
答案解析收藏纠错 + 选题
24. (2022七下·宁波开学考) 如图1，点O为直线AB上一点，过O点作射线OC，使∠AOC：∠BOC=1：2，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线的下方.
1. （1）将图1中的三角板绕点O按逆时针方向旋转至图2的位置，使得ON落在射线OB上，此时三角板旋转的角度为度；
2. （2）在上述直角三角板从图1逆时针旋转到图3的位置的过程中，若三角板绕点O按15°每秒的速度旋转，当直角三角板的直角边ON所在直线恰好平分∠AOC时，求此时三角板绕点O的运动时间t的值.
3. （3）将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的进程中，假如第t秒时，OA，OC，ON三条射线构成相等的角，求此时的值为多少？（直接写出答案）
答案解析收藏纠错 + 选题
25. (2022七下·义乌开学考) 定义“※”运算，观察下列运算：
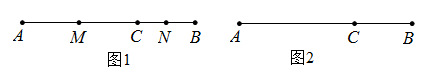
(+2)※(+13)=15，(-10)※(-12)=22；

(-5)※(+13)=-18，(+8)※(-10)=-18；

0※(+13)=-13，(-10)※0=10.
1. （1）请你认真思考上述运算，归纳“※”运算的法则：
  两数进行“※”运算时，同号，异号，并把绝对值；
  
  特别地，0和任何数进行“※”运算或任何数和0进行“※”运算，都得这个数的.
2. （2）计算：(-15)※[0※(+7)].
3. （3）若(2※a)×3+2＝4a，求a的值.
答案解析收藏纠错 + 选题
26. (2022七下·义乌开学考) 阅读理解：在钟面上，把一周分成12个大格，每个大格分成5个小格，所以每个大格对应的是30°角，每个小格对应的是6°角，时针每分钟转过的角度是0.5度，分针每分针转过的角度是6度.
解决问题：
1. （1）当时钟的时刻是8：30时，求此时分针与时针所夹的锐角的度数.
2. （2） 8：00开始几分钟后分针第一次追上时针.
3. （3）设在8：00时，分针的位置为OA，时针的位置为OB，运动后的分针为OP，时针为OQ.问：在8：00～9：00之间，从8：00开始运动几分钟，OB，OP，OQ这三条射线，其中一条射线是另外两条射线所夹的角的平分线？
答案解析收藏纠错 + 选题
27. (2022七下·蓬安开学考) 如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角板（∠D=30°）的直角顶点放在点O处，一边OE在射线OA上，另一边OD与OC都在直线AB的上方．
1. （1）将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周，如图2，经过t秒后，OD恰好平分∠BOC．
  ①此时t的值为 ▲ ；（直接填空）
  
  ②此时OE是否平分∠AOC？请说明理由；
2. （2）在（1）问的基础上，若三角板在转动的同时，射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠DOE？请说明理由；
3. （3）在（2）问的基础上，经过多长时间OC平分∠DOB？请画图并说明理由．
答案解析收藏纠错 + 选题
28. (2022八下·蓬安开学考) 平面直角坐标系中，点A(x，y)，且x²－8x＋16＋＝0，△ABC是以AB为斜边的等腰直角三角形(点A、B、C逆时针排列).
1. （1）直接写出点A的坐标是；
2. （2）如图1，已知点B(0，n)且0＜n＜4，连接OC. 求四边形ABOC的面积；
3. （3）如图2，已知点B(m，n)且0＜m＜4，0＜n＜4，过点A作AD⊥y轴于D，连接OB，M为OB的中点，连接DM、CM. 求证：DM⊥CM.
答案解析收藏纠错 + 选题
29. (2021七上·海曙期末) 如图为半圆形计时器，指针 $\text{[math]}$ 绕点 $\text{[math]}$ 从 $\text{[math]}$ 开始逆时针向 $\text{[math]}$ 旋转，速度为 $\text{[math]}$ 每秒，指针 $\text{[math]}$ 绕点 $\text{[math]}$ 从 $\text{[math]}$ 开始先顺时针向 $\text{[math]}$ 旋转，到达 $\text{[math]}$ 后再逆时针向回旋转，速度为 $\text{[math]}$ 每秒，两指针同时从起始位置出发，当 $\text{[math]}$ 到达时，两针都停止旋转。设旋转时间为 $\text{[math]}$ 秒
1. （1）求 $\text{[math]}$ 为何值时 $\text{[math]}$ 与 $\text{[math]}$ 首次重合；
2. （2）求 $\text{[math]}$ (用含 $\text{[math]}$ 的代数式表示)；
3. （3）直接写出 $\text{[math]}$ 时 $\text{[math]}$ 的值为.
答案解析收藏纠错 + 选题
30. (2021七上·韶关期末) 如图，点 $\text{[math]}$ ， $\text{[math]}$ 是数轴上两点，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ， $\text{[math]}$ ．动点 $\text{[math]}$ ， $\text{[math]}$ 分别从 $\text{[math]}$ ， $\text{[math]}$ 出发，点 $\text{[math]}$ 以每秒2个单位长度的速度沿数轴向右匀速运动，点 $\text{[math]}$ 以每秒1个单位长度的速度沿数轴向左匀速运动，设运动时间为 $\text{[math]}$ 秒．
1. （1）数轴上点 $\text{[math]}$ 表示的数是．
2. （2）求数轴上点 $\text{[math]}$ ， $\text{[math]}$ 表示的数（用含t的式子表示）．
3. （3）若点 $\text{[math]}$ 和 $\text{[math]}$ 同时出发，t为何值时，这两点相遇？
4. （4）若点 $\text{[math]}$ 比点 $\text{[math]}$ 迟2秒钟出发，则点 $\text{[math]}$ 出发几秒时，点 $\text{[math]}$ 和点 $\text{[math]}$ 刚好相距5个单位长度？
答案解析收藏纠错 + 选题

试卷信息