2022年全国中考数学真题分类汇编26 概率

更新时间：2022-12-29 浏览次数：100 类型：二轮复习

一、单选题

1. (2023七下·淄川期末) 如图，一张圆桌共有3个座位，甲、乙，丙3人随机坐到这3个座位上，则甲和乙相邻的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·抚州期末) 下列成语所描述的事件属于不可能事件的是（）

A . 水落石出 B . 水涨船高 C . 水滴石穿 D . 水中捞月

答案解析收藏纠错 + 选题
3. (2024九上·峡江期末) 9张背面相同的卡片，正面分别写有不同的从1到9的一个自然数，现将卡片背面朝上，从中任意抽出一张，正面的数是偶数的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·南宁模拟) 在一个不透明的袋子里，装有3个红球、1个白球，它们除颜色外都相同，从袋中任意摸出一个球为红球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·丽水) 老师从甲、乙、丙、丁四位同学中任选一人去学校劳动基地浇水，选中甲同学的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·绵阳) 某校开展岗位体验劳动教育活动，设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位，每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动，则这两名同学恰好在同一岗位体验的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·沈阳月考) 下列说法正确的是（）

A . 自然现象中，“太阳东方升起”是必然事件 B . 成语“水中捞月”所描述的事件，是随机事件 C . “襄阳明天降雨的概率为0.6”，表示襄阳明天一定降雨 D . 若抽奖活动的中奖概率为 $\text{[math]}$ ，则抽奖50次必中奖1次

答案解析收藏纠错 + 选题
8. (2024九下·长沙模拟) 下列说法正确的是（）

A . 为了解我国中小学生的睡眠情况，应采取全面调查的方式 B . 一组数据1，2，5，5，5，3，3的众数和平均数都是3 C . 若甲、乙两组数的方差分别是0.01，0.1，则甲组数据比乙组数据更稳定 D . 抛掷一枚硬币200次，一定有100次“正面向上”

答案解析收藏纠错 + 选题
9. (2024九下·石家庄模拟) 某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定，以抽签方式决定每个人的出场顺序，主持人将表示出场顺序的数字1，2，3分别写在3张同样的纸条上，并将这些纸条放在一个不透明的盒子中，搅匀后从中任意抽出一张，小星第一个抽，下列说法中正确的是（）

A . 小星抽到数字1的可能性最小 B . 小星抽到数字2的可能性最大 C . 小星抽到数字3的可能性最大 D . 小星抽到每个数的可能性相同

答案解析收藏纠错 + 选题

二、填空题

10. (2022·盐城) 如图所示，电路图上有A，B，C三个开关和一个小灯泡，闭合开关C或者同时闭合开关A，B，都可使小灯泡发光．现任意闭合其中一个开关，则小灯泡发光的概率等于

答案解析收藏纠错 + 选题
11. (2023九上·越城期末) 不透明袋子里装有仅颜色不同的 4 个白球和2个红球，从袋子中随机摸出一球，“摸出红球”的概率是．

答案解析收藏纠错 + 选题
12. (2022·嘉兴) 不透明的袋子中装有5个球，其中有3个红球和2个黑球，它们除颜色外都相同.从袋子中随机取出1个球，则它是黑球的概率是．

答案解析收藏纠错 + 选题
13. (2023·仙居模拟) 将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）掷一次，朝上一面点数是1的概率为．

答案解析收藏纠错 + 选题
14. (2023九上·诸暨月考) 一个不透明的袋子里装有5个红球和6个白球，它们除颜色外其余都相同．从袋中任意摸出一个球是红球的概率为

答案解析收藏纠错 + 选题
15. (2024九下·深圳模拟) 一个不透明的箱子里放着分别标有数字1，2，3，4，5，6的六个球，它们除了数字外其余都相同．从这个箱子里随机摸出一个球，摸出的球上所标数字大于4的概率是

答案解析收藏纠错 + 选题
16. (2024九上·嵊州期中) 有5张仅有编号不同的卡片，编号分别是1，2，3，4，5．从中随机抽取一张，编号是偶数的概率等于

答案解析收藏纠错 + 选题
17. (2022·金华) 一个布袋里装有7个红球、3白球，它们除颜色外都相同.从中任意摸出1个球，摸到红球的概率是.

答案解析收藏纠错 + 选题
18. (2024九下·同安模拟) 不透明的袋子中装有5个球，其中有3个红球和2个黑球，它们除颜色外都相同。从袋子中随机取出1个球，它是黑球的概率是.

答案解析收藏纠错 + 选题
19. (2022·攀枝花) 盒子里装有除颜色外，没有其他区别的2个红球和2个黑球，搅匀后从中取出1个球，放回搅匀再取出第2个球，则两次取出的球是1红1黑的概率为.

答案解析收藏纠错 + 选题
20. (2023九下·潮南模拟) 投掷一枚六个面分别标有1、2、3、4、5、6的质地均匀的正方体骰子，则偶数朝上的概率是．

答案解析收藏纠错 + 选题
21. (2022·贵阳) 端午节到了，小红煮好了10个粽子，其中有6个红枣粽子，4个绿豆粽子.小红想从煮好的粽子中随机捞一个，若每个粽子形状完全相同，被捞到的机会相等，则她捞到红枣粽子的概率是.

答案解析收藏纠错 + 选题

三、解答题

22. (2022·盐城) 某社区举行新冠疫情防控核酸检测大演练，卫生防疫部门在该社区设置了三个核酸检测点A、B、C，甲、乙两人任意选择一个检测点参加检测．求甲、乙两人不在同一检测点参加检测的概率．（用画树状图或列表的方法求解）

答案解析收藏纠错 + 选题
23. (2022·泰州) 即将在泰州举办的江苏省第20届运动会带动了我市的全民体育热，小明去某体育馆锻炼，该体育馆有A、B两个进馆通道和C、D、E三个出馆通道，从进馆通道进馆的可能性相同，从出馆通道出馆的可能性也相同.用列表或画树状图的方法，列出小明一次经过进馆通道与出馆通道的所有等可能的结果，并求他恰好经过通道A与通道D的概率.

答案解析收藏纠错 + 选题

四、综合题

24. (2023九上·从江期中) 一只不透明的袋子中装有3个大小、质地完全相同的乒乓球，球面上分别标有数字1、2、3，搅匀后先从袋子中任意摸出1个球，记下数字后放回，搅匀后再从袋子中任意摸出1个球，记下数字.
1. （1）第一次摸到标有偶数的乒乓球的概率是；
2. （2）用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.
答案解析收藏纠错 + 选题
25. (2022·徐州) 如图，将下列3张扑克牌洗匀后数字朝下放在桌面上．
1. （1）从中随机抽取1张，抽得扑克牌上的数字为3的概率为；
2. （2）从中随机抽取2张，用列表或画树状图的方法，求抽得2张扑克牌的数字不同的概率．
答案解析收藏纠错 + 选题
26. (2023·德惠模拟) 一只不透明的袋子中装有2个白球、1个红球，这些球除颜色外都相同．
1. （1）搅匀后从中任意摸出一个球，摸到红球的概率等于；
2. （2）搅匀后从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出一个球．用列表或画树状图的方法，求2次都摸到红球的概率．
答案解析收藏纠错 + 选题
27. (2022·南通) 不透明的袋子中装有红球、黄球、蓝球各一个，这些球除颜色外无其他差别．
1. （1）从袋子中随机摸出一个球，摸到蓝球的概率是；
2. （2）从袋子中随机摸出一个球后，放回并摇匀，再随机摸出一个球．求两次摸到的球的颜色为“一红一黄”的概率．
答案解析收藏纠错 + 选题
28. (2022九上·碑林月考) 建国中学有7位学生的生日是10月1日，其中男生分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，女生分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .学校准备召开国庆联欢会，计划从这7位学生中抽取学生参与联欢会的访谈活动.
1. （1）若任意抽取1位学生，且抽取的学生为女生的概率是；
2. （2）若先从男生中任意抽取1位，再从女生中任意抽取1位，求抽得的2位学生中至少有1位是 $\text{[math]}$ 或 $\text{[math]}$ 的概率.（请用“画树状图”或“列表”等方法写出分析过程）
答案解析收藏纠错 + 选题
29. (2023九上·茂名期中) 一只不透明的袋子中装有1个白球，3个红球，这些球除颜色外都相同.
1. （1）搅匀后从中任意摸出1个球，这个球是白球的概率为；
2. （2）搅匀后从中任意摸出1个球，记录颜色后放回，搅匀，再从中任意摸出1个球，求2次摸到的球恰好是1个白球和1个红球的概率.（请用画树状图或列表等方法说明理由）
答案解析收藏纠错 + 选题
30. (2022·扬州) 某超市为回馈广大消费者，在开业周年之际举行摸球抽奖活动.摸球规则如下：在一只不透明的口袋中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后先从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球.
1. （1）用树状图列出所有等可能出现的结果；
2. （2）活动设置了一等奖和二等奖两个奖次，一等奖的获奖率低于二等奖.现规定摸出颜色不同的两球和摸出颜色相同的两球分别对应不同奖次，请写出它们分别对应的奖次，并说明理由.
答案解析收藏纠错 + 选题
31. (2024九下·九江期中) 从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛，求下列事件发生的概率.
1. （1）甲一定参加比赛，再从其余3名学生中任意选取1名，恰好选中丙的概率是；
2. （2）任意选取2名学生参加比赛，求一定有乙的概率.（用树状图或列表的方法求解）.
答案解析收藏纠错 + 选题
32. (2024·昆明模拟) “石头、剪子、布”是一个广为流传的游戏，规则是：甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种，其中“石头”赢“剪子”，“剪子”赢“布”，“布”赢“石头”，手势相同不分输赢.假设甲、乙两人每次都随意并且同时做出3种手势中的1种.
1. （1）甲每次做出“石头”手势的概率为；
2. （2）用画树状图或列表的方法，求乙不输的概率.
答案解析收藏纠错 + 选题

33. (2022·内江) 为让同学们了解新冠病毒的危害及预防措施，某中学举行了“新冠病毒预防”知识竞赛.数学课外活动小组将八（1）班参加本校知识竞赛的40名同学的成绩（满分为100分，得分为正整数且无满分，最低为75分）分成五组进行统计，并绘制了下列不完整的统计图表：

分数段	频数	频率
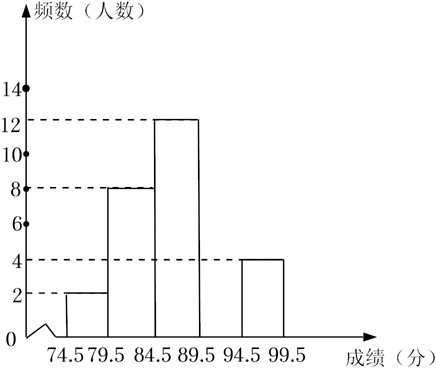
74.5﹣79.5	2	0.05
79.5﹣84.5	8	n
84.5﹣89.5	12	0.3
89.5﹣94.5	m	0.35
94.5﹣99.5	4	0.1

（1）表中m＝，n＝；
（2）请补全频数分布直方图；
（3）本次知识竞赛中，成绩在94.5分以上的选手，男生和女生各占一半，从中随机确定2名学生参加颁奖，请用列表法或树状图法求恰好是一名男生和一名女生的概率.

答案解析收藏纠错 + 选题

34. (2022·广安) 某校在开展线上教学期间，为了解七年级学生每天在家进行体育活动的时间（单位：h），随机调查了该年级的部分学生.根据调查结果，绘制出如下的扇形统计图1和条形统计图2，请根据相关信息，解答下列问题：
1. （1）本次随机调查的学生共有人，图1中m的值为.
2. （2）请补全条形统计图
3. （3）体育活动时间不足1小时的四人中有3名女生A₁、A₂、A₃和1名男生B.为了解他们在家体育活动的实际情况，从这4人中随机抽取2人进行电话回访，请用列表法或画树状图法，求恰好抽到两名女生的概率
答案解析收藏纠错 + 选题
35. (2022·恩施) 2022年4月29日，湖北日报联合夏风教室发起“劳动最光荣，加油好少年”主题活动。某校学生积极参与本次主题活动，为了解该校学生参与本次主题活动的情况，随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图。请结合图中信息解答下列问题：
1. （1）本次共调查了名学生，并补全条形统计图.
2. （2）若该校共有1200名学生参加本次主题活动，则本次活动中该校“洗衣服”的学生约有多少名？
3. （3）现从参与本次主题活动的甲、乙、丙、丁4名学生中，随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法，求甲、乙两人同时被抽中的概率.
答案解析收藏纠错 + 选题
36. (2022·鄂州) 为庆祝中国共产主义青年团成立100周年，某校举行了“青年大学习，强国有我”知识竞赛活动.李老师赛后随机抽取了部分学生的成绩（单位：分，均为整数），按成绩划分为A，B，C，D四个等级，并制作了如下统计图表（部分信息未给出）：
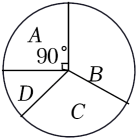
等级
成绩x/分
人数
A
90≤x≤100
15
B
80≤x＜90
a
C
70≤x＜80
18
D
x＜70
7
1. （1）表中a＝，C等级对应的圆心角度数为；
2. （2）若全校共有600名学生参加了此次竞赛，成绩A等级的为优秀，则估计该校成绩为A等级的学生共有多少人？
3. （3）若A等级15名学生中有3人满分，设这3名学生分别为T₁ ， T₂ ， T₃ ，从其中随机抽取2人参加市级决赛，请用列表或树状图的方法求出恰好抽到T₁ ， T₂的概率.
答案解析收藏纠错 + 选题

37. (2023·浙江模拟) 某兴趣小组针对视力情况随机抽取本校部分学生进行调查，将调查结果进行统计分析，绘制成如下不完整的统计图表.

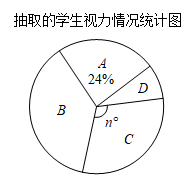
抽取的学生视力情况统计表

类别	调查结果	人数
A	正常	48
B	轻度近视	76
C	中度近视	60
D	重度近视	m

请根据图表信息解答下列问题：

（1）填空：m= ，n= ；
（2）该校共有学生1600人，请估算该校学生中“中度近视”的人数；
（3）某班有四名重度近视的学生甲、乙、丙、丁，从中随机选择两名学生参加学校组织的“爱眼护眼”座谈会，请用列表或画树状图的方法求同时选中甲和乙的概率.

答案解析收藏纠错 + 选题

38. (2023·大朗模拟) 为弘扬荆州传统文化，我市将举办中小学生“知荆州、爱荆州、兴荆州”知识竞赛活动.某校举办选拔赛后，随机抽取了部分学生的成绩，按成绩（百分制）分为A，B，C，D四个等级，并绘制了如下不完整的统计图表.

等级

成绩（x）

人数

A

$\text{[math]}$

m

B

$\text{[math]}$

24

C

$\text{[math]}$

14

D

$\text{[math]}$

10

根据图表信息，回答下列问题：
1. （1）表中m＝；扇形统计图中，B等级所占百分比是，C等级对应的扇形圆心角为度；
2. （2）若全校有1400人参加了此次选拔赛，则估计其中成绩为A等级的共有人；
3. （3）若全校成绩为100分的学生有甲、乙、丙、丁4人，学校将从这4人中随机选出2人参加市级竞赛.请通过列表或画树状图，求甲、乙两人至少有1人被选中的概率.
答案解析收藏纠错 + 选题
39. (2022·六盘水) 为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
教职工气排球比赛比分胜负表
1. （1）根据表中数据可知，一中共获胜场，“四中VS五中”的比赛获胜可能性最大的是；
2. （2）若 $\text{[math]}$ 处的比分是21∶10和21∶8，并且参加决赛的队伍是二中和五中，则 $\text{[math]}$ 处的比分可以是和；（两局结束比赛，根据自己的理解填写比分）；
3. （3）若 $\text{[math]}$ 处的比分是10∶21和8∶21， $\text{[math]}$ 处的比分是21∶18，15∶21，15∶12，那么实力最强的是哪两支队伍，请说明理由．
答案解析收藏纠错 + 选题
40. (2022·黔西) 神舟十四号载人飞船的成功发射，再次引发校园科技热．光明中学准备举办“我的航天梦”科技活动周，在全校范围内邀请有兴趣的学生参加以下四项活动，A：航模制作；B：航天资料收集；C：航天知识竞赛；D：参观科学馆．为了了解学生对这四项活动的参与意愿，学校随机调查了该校有兴趣的m名学生（每名学生必选一项且只能选择一项），并将调查的结果绘制成如下两幅不完整的统计图．
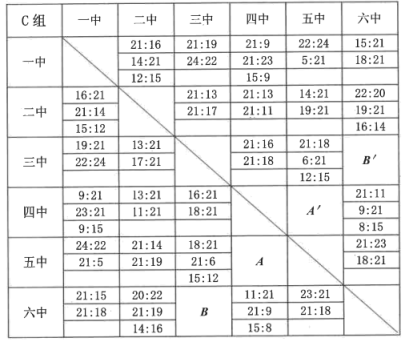
根据以上信息，解答下列问题：
1. （1） $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ；并补全条形统计图：
2. （2）根据抽样调查的结果，请估算全校1800名学生中，大约有多少人选择参观科学馆；
3. （3）在选择A项活动的10人中，有甲、乙、丙、丁四名女生，现计划把这10名学生平均分成两组进行培训，每组各有两名女生，则甲、乙被分在同一组的概率是多少？
答案解析收藏纠错 + 选题