B .
B .  C .
C . 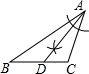 D .
D . 




 B .
B . 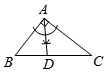 C .
C . 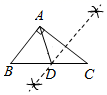 D .
D . 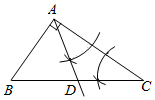
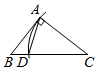
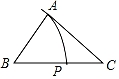
①以点 为圆心,以
为半径画弧,以点
为圆心,以
为半径画弧,两弧交于
点;②作线段
等于
;③连接
,
,则
就是所求作图形.


⑴直接判断的形状.
⑵画出关于直线
的对称图形△
.
⑶在直线上作一点
, 使得
最小,

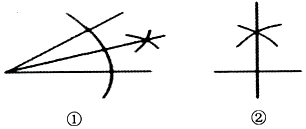
 B .
B . 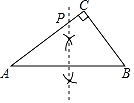 C .
C . 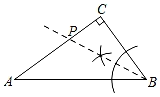 D .
D . 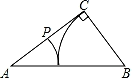


 B .
B . 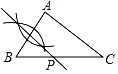 C .
C .  D .
D . 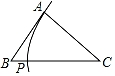



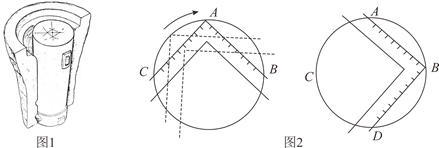
问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎范、芯组成的(如图1),它的端面是圆形,如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记A,B,C三点;将“矩”向右旋转,使它左侧边落在A,B点上,“矩”的另一条边与圆的交点标记为D点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,连接AD,BC相交于点O,即O为圆心.