2023年中考数学精选真题实战测试45 四边形综合题 A

更新时间：2023-02-18 浏览次数：95 类型：二轮复习

一、单选题（每题3分，共30分）

1. (2022·菏泽) 如图，在菱形ABCD中， $\text{[math]}$ ， M是对角线BD上的一个动点， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
2. (2023·泰州模拟) 如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动.设点P的运动时间为t（单位：s），下列结论正确的是（）

A . 当 $\text{[math]}$ 时，四边形ABMP为矩形 B . 当 $\text{[math]}$ 时，四边形CDPM为平行四边形 C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$ 或6s

答案解析收藏纠错 + 选题
3. (2023九上·峄城月考) 若顺次连接四边形 $\text{[math]}$ 各边的中点所得的四边形是正方形，则四边形 $\text{[math]}$ 的两条对角线 $\text{[math]}$ 一定是（）

A . 互相平分 B . 互相垂直 C . 互相平分且相等 D . 互相垂直且相等

答案解析收藏纠错 + 选题
4. (2022·随州) 七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点， $\text{[math]}$ 分别交BD，EF于O，P两点，M，N分别为BO，DC的中点，连接AP，NF，沿图中实线剪开即可得到一副七巧板，则在剪开之前，关于该图形，下列说法：①图中的三角形都是等腰直角三角形；②四边形MPEB是菱形；③四边形PFDM的面积占正方形ABCD面积的 $\text{[math]}$ .正确的有（）

A . 只有① B . ①② C . ①③ D . ②③

答案解析收藏纠错 + 选题
5. (2022·敖汉旗模拟) 如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2 $\text{[math]}$ ，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM＝x，则S关于x的函数图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022·东营) 如图，已知菱形 $\text{[math]}$ 的边长为2，对角线 $\text{[math]}$ 相交于点O，点M，N分别是边 $\text{[math]}$ 上的动点， $\text{[math]}$ ，连接 $\text{[math]}$ .以下四个结论正确的是（）
① $\text{[math]}$ 是等边三角形；② $\text{[math]}$ 的最小值是 $\text{[math]}$ ；③当 $\text{[math]}$ 最小时 $\text{[math]}$ ；④当 $\text{[math]}$ 时， $\text{[math]}$ .

A . ①②③ B . ①②④ C . ①③④ D . ①②③④

答案解析收藏纠错 + 选题
7. (2023八下·盐城月考) 如图，已知矩形ABCD的边长分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形 $\text{[math]}$ ；第二次，顺次连接四边形 $\text{[math]}$ 各边的中点，得到四边形 $\text{[math]}$ ；…如此反复操作下去，则第n次操作后，得到四边形 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·黄冈) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ ，分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧交于点 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 下列结论：
$\text{[math]}$ 四边形 $\text{[math]}$ 是菱形； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 若 $\text{[math]}$ 平分 $\text{[math]}$ ，则 $\text{[math]}$ .

其中正确结论的个数是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
9. (2022·清苑模拟) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，把边AB沿对角线BD平移，点 $\text{[math]}$ ， $\text{[math]}$ 分别对应点A，B.给出下列结论：①顺次连接点 $\text{[math]}$ ， $\text{[math]}$ ，C，D的图形是平行四边形；②点C到它关于直线 $\text{[math]}$ 的对称点的距离为48；③ $\text{[math]}$ 的最大值为15；④ $\text{[math]}$ 的最小值为 $\text{[math]}$ .其中正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2022·烟台模拟) 如图， $\text{[math]}$ 是边长为1的等边三角形，D、E为线段AC上两动点，且 $\text{[math]}$ ，过点D、E分别作AB、BC的平行线相交于点F ，分别交BC、AB于点H、G ．现有以下结论：① $\text{[math]}$ ；②当点D与点C重合时， $\text{[math]}$ ；③ $\text{[math]}$ ；④当 $\text{[math]}$ 时，四边形BHFG为菱形，其中正确结论为（）

A . ①②③ B . ①②④ C . ①②③④ D . ②③④

答案解析收藏纠错 + 选题

二、填空题（每空3分，共18分）

11. (2022九上·乐山期中) 利用图形的分、和、移、补探索图形关系，是我国传统数学的一种重要方法．如图1，BD是矩形ABCD的对角线，将△BCD分割成两对全等的直角三角形和一个正方形，然后按图2重新摆放，观察两图，若a＝4，b＝2，则矩形ABCD的面积是．

答案解析收藏纠错 + 选题
12. (2023·即墨模拟) 如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且 $\text{[math]}$ ，连接EF交边AD于点G．过点A作 $\text{[math]}$ ，垂足为点M，交边CD于点N．若 $\text{[math]}$ ， $\text{[math]}$ ，则线段AN的长为

答案解析收藏纠错 + 选题
13. (2023·兴隆台模拟) 如图，正方形 $\text{[math]}$ 的对角线相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2023九上·凤翔月考) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的一个动点，则 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题
15. (2022·南通) 如图，点O是正方形 $\text{[math]}$ 的中心， $\text{[math]}$ ． $\text{[math]}$ 中， $\text{[math]}$ 过点D， $\text{[math]}$ 分别交 $\text{[math]}$ 于点G，M，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题
16. (2021·赤峰) 如图，正方形ABCD的边长为 $\text{[math]}$ ，点E是BC的中点，连接CG并延长，交AB于点F ，连接AH ．以下结论：①CF⊥DE；② $\text{[math]}$ ；③ $\text{[math]}$ ，④ $\text{[math]}$ ，其中正确结论的序号是．

答案解析收藏纠错 + 选题

三、解答题（共7题，共72分）

17. (2022·广州) 如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．
1. （1）求BD的长；
2. （2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE= $\text{[math]}$ DF，
  ①当CE丄AB时，求四边形ABEF的面积；
  
  ②当四边形ABEF的面积取得最小值时，CE+ $\text{[math]}$ CF的值是否也最小？如果是，求CE+ $\text{[math]}$ CF的最小值；如果不是，请说明理由．
答案解析收藏纠错 + 选题

18. (2022九上·南宁月考) 矩形ABCD中， $\text{[math]}$ ＝ $\text{[math]}$ （k＞1），点E是边BC的中点，连接AE，过点E作AE的垂线EF，与矩形的外角平分线CF交于点F．

（1）【特例证明】如图（1），当k＝2时，求证：AE＝EF；

小明不完整的证明过程如下，请你帮他补充完整．

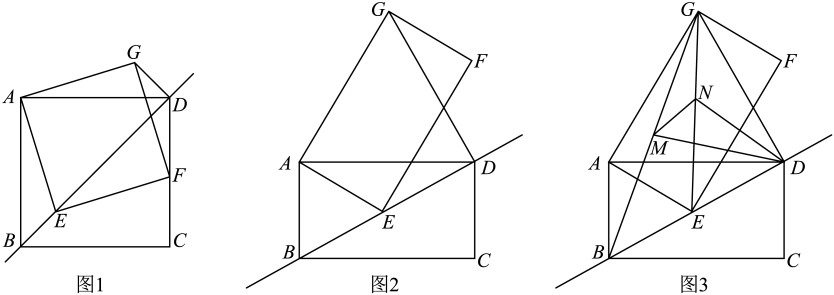
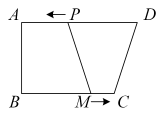
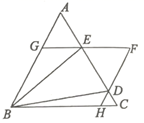
证明：如图，在BA上截取BH＝BE，连接EH．

∵k＝2，

∴AB＝BC．

∵∠B＝90°，BH＝BE，

∴∠1＝∠2＝45°，

∴∠AHE＝180°-∠1＝135°．

∵CF平分∠DCG，∠DCG＝90°，

∴∠3＝ $\text{[math]}$ ∠DCG＝45°．

∴∠ECF＝∠3+∠4＝135°．

∴……

（只需在答题卡对应区域写出剩余证明过程）

（2）【类比探究】如图（2），当k≠2时，求 $\text{[math]}$ 的值（用含k的式子表示）；
（3）【拓展运用】如图（3），当k＝3时，P为边CD上一点，连接AP，PF，∠PAE＝45°， $\text{[math]}$ ，求BC的长．

答案解析收藏纠错 + 选题

19. (2022·长春) 【探索发现】在一次折纸活动中，小亮同学选用了常见的A4纸，如图①，矩形 $\text{[math]}$ 为它的示意图．他查找了A4纸的相关资料，根据资料显示得出图①中 $\text{[math]}$ ．他先将A4纸沿过点A的直线折叠，使点B落在 $\text{[math]}$ 上，点B的对应点为点E，折痕为 $\text{[math]}$ ；再沿过点F的直线折叠，使点C落在 $\text{[math]}$ 上，点C的对应点为点H，折痕为 $\text{[math]}$ ；然后连结 $\text{[math]}$ ，沿 $\text{[math]}$ 所在的直线再次折叠，发现点D与点F重合，进而猜想 $\text{[math]}$ ．
1. （1）【问题解决】
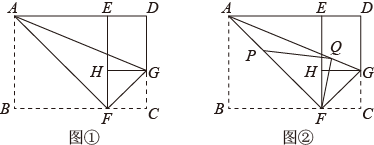
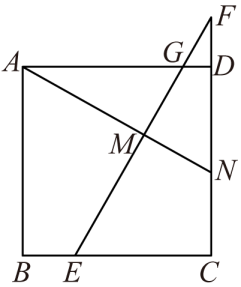
  小亮对上面 $\text{[math]}$ 的猜想进行了证明，下面是部分证明过程：
  
  证明：四边形 $\text{[math]}$ 是矩形，
  
  ∴ $\text{[math]}$ ．
  
  由折叠可知， $\text{[math]}$ ， $\text{[math]}$ ．
  
  ∴ $\text{[math]}$ ．
  
  ∴ $\text{[math]}$ ．
  
  请你补全余下的证明过程．
2. （2）【结论应用】
  $\text{[math]}$ 的度数为度， $\text{[math]}$ 的值为；
3. （3）在图①的条件下，点P在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ，点Q在线段 $\text{[math]}$ 上，连结 $\text{[math]}$ 、 $\text{[math]}$ ，如图②，设 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．（用含a的代数式表示）
答案解析收藏纠错 + 选题
20. (2023·抚顺模拟) 已知矩形ABCD，点E为直线BD上的一个动点（点E不与点B重合），连接AE，以AE为一边构造矩形AEFG（A，E，F，G按逆时针方向排列），连接DG．
1. （1）如图1，当 $\text{[math]}$ ＝ $\text{[math]}$ ＝1时，请直接写出线段BE与线段DG的数量关系与位置关系；
2. （2）如图2，当 $\text{[math]}$ ＝ $\text{[math]}$ ＝2时，请猜想线段BE与线段DG的数量关系与位置关系，并说明理由；
3. （3）如图3，在（2）的条件下，连接BG，EG，分别取线段BG，EG的中点M，N，连接MN，MD，ND，若AB＝ $\text{[math]}$ ， ∠AEB＝45°，请直接写出△MND的面积．
答案解析收藏纠错 + 选题
21. (2022·益阳) 如图，矩形ABCD中，AB＝15，BC＝9，E是CD边上一点（不与点C重合），作AF⊥BE于F，CG⊥BE于G，延长CG至点C′，使C′G＝CG，连接CF，AC′．
1. （1）直接写出图中与△AFB相似的一个三角形；
2. （2）若四边形AFCC′是平行四边形，求CE的长；
3. （3）当CE的长为多少时，以C′，F，B为顶点的三角形是以C′F为腰的等腰三角形？
答案解析收藏纠错 + 选题
22. (2024·临沂一模) $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，点E、D分别从点A，B同时出发，以相同的速度沿 $\text{[math]}$ 运动，运动到点B、C停止.
1. （1）如图1，当点E、D分别与点A、B重合时，请判断：线段 $\text{[math]}$ 的数量关系是，位置关系是；
2. （2）如图2，当点E、D不与点A，B重合时，（1）中的结论是否依然成立？若成立，请给予证明；若不成立，请说明理由；
3. （3）当点D运动到什么位置时，四边形 $\text{[math]}$ 的面积是 $\text{[math]}$ 面积的一半，请直接写出答案；此时，四边形 $\text{[math]}$ 是哪种特殊四边形？请在备用图中画出图形并给予证明.
答案解析收藏纠错 + 选题
23. (2022·衢州) 如图，在菱形ABCD中，AB=5，BD为对角线.点E是边AB延长线上的任意一点，连结DE交BC于点F，BG平分∠CBE交DE于点G．
1. （1）求证： $\text{[math]}$ .
2. （2）若 $\text{[math]}$ ．
  ①求菱形 $\text{[math]}$ 的面积.
  
  ②求 $\text{[math]}$ 的值.
3. （3）若 $\text{[math]}$ ，当 $\text{[math]}$ 的大小发生变化时（ $\text{[math]}$ ），在AE上找一点T，使GT为定值，说明理由并求出ET的值．
答案解析收藏纠错 + 选题