备考2023年中考数学温州卷变式阶梯训练：第22题

更新时间：2023-04-15 浏览次数：103 类型：三轮冲刺

一、原题

1. (2022·温州) 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．
1. （1）求证：四边形 DEFG 是平行四边形．
2. （2）当AD=5，tan∠EDC= $\text{[math]}$ =时，求 FG 的长．
答案解析收藏纠错 + 选题

二、基础

2. (2022·舟山九上月考) 如图，在 $\text{[math]}$ 中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且 $\text{[math]}$ ，连接DB，EF．若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
1. （1）求证： $\text{[math]}$ ；
2. （2）求四边形DEFB的周长．
答案解析收藏纠错 + 选题
3. (2022八下·竞秀期末) 如图，在 $\text{[math]}$ 中，D、E分别为AB、AC的中点，过点C作 $\text{[math]}$ 交DE的延长线于点F．
1. （1）求证：四边形BCFD为平行四边形；
2. （2）若 $\text{[math]}$ ，求EF的长．
答案解析收藏纠错 + 选题
4. (2022八下·定远期末) 如图，在▱ABCD中，点E在边AD上，连接EB并延长至F，使BF＝BE；连接EC并延长至G，使CG＝CE，连接FG，点H为FG的中点，连接DH，AF．
1. （1）若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；
2. （2）求证：四边形AFHD为平行四边形．
答案解析收藏纠错 + 选题
5. (2022八下·大荔期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，延长BA到点D，使 $\text{[math]}$ ，点E、F分别为边BC、AC的中点．
1. （1）求证： $\text{[math]}$ ；
2. （2）过点A作 $\text{[math]}$ ，交DF于点G，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
6. (2022·泰州) 如图，线段DE与AF分别为△ABC的中位线与中线.
1. （1）求证：AF与DE互相平分；
2. （2）当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由.
答案解析收藏纠错 + 选题
7. (2022八下·余姚期中) 如图，点D、E、F分别是△ABC的边AB、BC、AC的中点，延长DE至点G，使得DE=EG，连接AE，FG.
1. （1）求证：四边形AEGF是平行四边形．
2. （2）若∠BAC＝90°，AD＝AC＝ $\text{[math]}$ ，求FG的长．
答案解析收藏纠错 + 选题
8. (2022八下·黄冈期中) 如图，点O是△ABC内一点，连接OA、OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连接，得到四边形DEFG．
1. （1）求证：四边形DEFG是平行四边形；
2. （2）若BO上CO，M为EF的中点，且OA＝8，OM＝3，求四边形DEFG的周长．
答案解析收藏纠错 + 选题
9. (2022八下·诸暨期中) 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使 $\text{[math]}$ ，连接EC并延长，使 $\text{[math]}$ ，连接FG，H为FG的中点，连接DH
1. （1）求证：四边形AFHD为平行四边形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题

三、进阶

10. (2022八下·惠州期末) 如图，在Rt△ABC中，∠ACB＝90°，D、E分别是边AC、AB的中点，连接CE、DE，过D点作DF∥CE交BC的延长线于F点．
1. （1）证明：四边形DECF是平行四边形；
2. （2）若AB＝13cm，AC＝5cm，求四边形DECF的周长．
答案解析收藏纠错 + 选题
11. (2021八下·泉港期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 的中点.
1. （1）求作一点 $\text{[math]}$ ，使得点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 对称；（要求：尺规作图，保留痕迹，不写作法）
2. （2）连接 $\text{[math]}$ ，请写出线段 $\text{[math]}$ 、 $\text{[math]}$ 之间的关系，并证明.
答案解析收藏纠错 + 选题
12. (2022·道外模拟) 如图，已知CD为△ABC中线，E为CD上一点，连接AE并延长至点F，使 $\text{[math]}$ ，连接BF、CF， $\text{[math]}$ ．
1. （1）求证：四边形DBFC是平行四边形．
2. （2）设四边形ABFC的面积为S，在不添加任何辅助线的情况下，请写出图中四个面积等于 $\text{[math]}$ 的三角形．
答案解析收藏纠错 + 选题
13. (2022·烟台模拟) 已知，如图，在平行四边形ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上，且AE=CF．
1. （1）求证：四边形EGFH是平行四边形．
2. （2）连结BD交AC于点O，若BD=12，AE=EF-CF，求EG的长．
答案解析收藏纠错 + 选题
14. (2022八下·东莞期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的长；
2. （2）求证： $\text{[math]}$ ；
3. （3）求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
15. (2020·资兴模拟) 如图，在Rt⊿ABC中，∠ACB是直角， tan∠B= $\text{[math]}$ ，BC=16 cm，点D以2cm/s的速度由点A向点B匀速运动，到达点B即停止，M、N分别是AD、CD的中点，连结MN，设点D的运动时间为t
1. （1）求MN的长；
2. （2）求点D由点A到点B匀速运动过程中，线段MN所扫过的面积；
3. （3）若⊿DMN是等腰三角形时，求t的值．
答案解析收藏纠错 + 选题
16. (2021八下·锦州期末) （问题情境）
如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，D是 $\text{[math]}$ 边上一点，过点D作 $\text{[math]}$ 交 $\text{[math]}$ 于点E，以D为顶点， $\text{[math]}$ 为一边作 $\text{[math]}$ ，使其另一边与 $\text{[math]}$ 边交于点F， $\text{[math]}$ 与 $\text{[math]}$ 交于点G．
1. （1）求证：G是 $\text{[math]}$ 的中点；
2. （2） M，N分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，求证：点G在线段 $\text{[math]}$ 上；
3. （3）（迁移拓展）
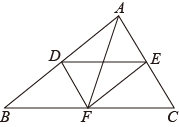
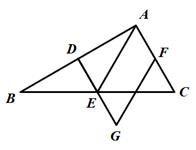
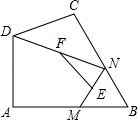
  如图2，已知D是长为4的线段 $\text{[math]}$ 上的动点（D不与A，B重合），分别以 $\text{[math]}$ ， $\text{[math]}$ 为边在线段 $\text{[math]}$ 的同侧作等边 $\text{[math]}$ 和等边 $\text{[math]}$ ，G为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
  
  ①请直接写出 $\text{[math]}$ 的最小值；（不要求写解题过程）
  
  ②请写出解题过程中需要的辅助线作法，并在图2中画出相应的辅助线．
答案解析收藏纠错 + 选题

四、突破

17. (2022八下·嘉兴期末) 如图，经过坐标原点O的直线交反比例函数 $\text{[math]}$ 的图象于点A（﹣2，3），B．点C是x轴上异于点O的动点，点D与点C关于y轴对称，射线AC交y轴于点E，连结AD，BC，BD．
1. （1） ①写出点B的坐标．
  ②求证：四边形ACBD是平行四边形．
2. （2）当四边形ACBD是矩形时，求点C的坐标．
3. （3）点C在运动过程中，当A，C，E三点中的其中一点到另两点的距离相等时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
18. (2021·普定模拟) 如图
1. （1）如图，已知△ABC中，D、E分别是AB、AC的中点，求证：DE∥BC，DE= $\text{[math]}$ BC.
2. （2）利用第（1）题的结论，解决下列问题：
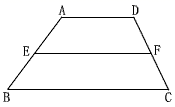
  ①如图，在四边形ABCD中，AD∥BC，E、F分别是AB、CD的中点，求证：EF∥BC，FE= $\text{[math]}$ （AD+BC）
  
  ②如图，在四边形ABCD中，∠A＝90°，AB＝3 $\text{[math]}$ ，AD＝3，点M，N分别在边AB，BC上，点E，F分别为MN，DN的中点，连接EF，求EF长度的最大值.
答案解析收藏纠错 + 选题

19. (2022·桐乡模拟) 教材呈现：浙教版八年级下册数学教材第98页的部分内容：

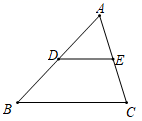
连结三角形两边中点的线段叫做三角形的中位线.如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点， $\text{[math]}$ 就是 $\text{[math]}$ 的一条中位线.我们可得到下面三角形的中位线定理：

三角形的中位线平行于第三边，并且等于第三边的一半.

已知：如图， $\text{[math]}$ 是 $\text{[math]}$ 的中位线.

求证： $\text{[math]}$ 且 $\text{[math]}$ .

（1）请根据教材内容，结合图1，写出证明过程：
（2）如图2，等腰直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转一周，点 $\text{[math]}$ ， $\text{[math]}$ 的对应点分别是 $\text{[math]}$ ， $\text{[math]}$ ，连结 $\text{[math]}$ ，设 $\text{[math]}$ 的中点为 $\text{[math]}$ ，在旋转过程中，点 $\text{[math]}$ 和点 $\text{[math]}$ 之间的距离会变化吗？若变化，请说明理由，若不变化，请求出这个距离的值；
（3）在（2）的旋转过程中，连结 $\text{[math]}$ 如图3，求 $\text{[math]}$ 度数的取值范围.

答案解析收藏纠错 + 选题

20. (2022九下·衢州开学考) 爱好思考的小实在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”，如图1、图2、图3中，AF、BE是△ABC的中线，AF⊥BE于点P，像△ABC这样的三角形均为“中垂三角形”，设BC＝a，AC＝b，AB＝c.
1. （1）【特例探究】
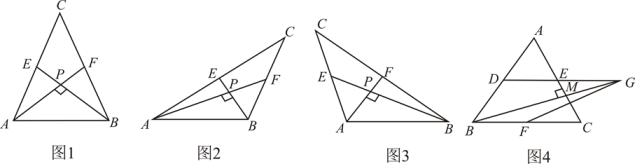
  ①如图1，当tan∠PAB＝1， $\text{[math]}$ 时，a＝，b＝.
  
  ②如图2，当∠PAB＝30°，c＝4时，a＝，b＝.
2. （2）【归纳证明】
  请你观察（1）中的计算结果，猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三者之间的关系，用等式表示出来，并利用图3证明你的结论.
3. （3）【拓展证明】
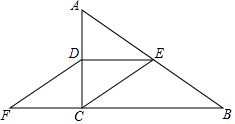
  如图4，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ，D、E、F分别是边AB、AC、BC的中点，连结DE并延长至点G，使得GE＝DE，连结BG.若BG⊥AC于点M时，求GF的长.
答案解析收藏纠错 + 选题
21. (2020·陕西模拟) 某校组织数学兴趣探究活动，爱思考的小实同学在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中， $\text{[math]}$ 、 $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 于点 $\text{[math]}$ ，像 $\text{[math]}$ 这样的三角形均称为“中垂三角形”.
1. （1）（特例探究）
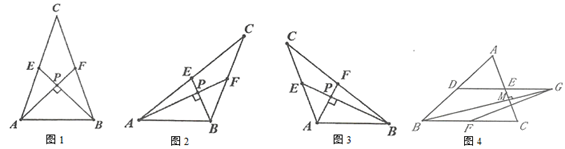
  如图1，当 $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ；
  
  如图2，当 $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）（归纳证明）
  请你观察（1）中的计算结果，猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三者之间的关系，用等式表示出来，并利用图3证明你的结论；
3. （3）（拓展证明）
  如图4，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ $\text{[math]}$ 的中点，连结 $\text{[math]}$ 并延长至 $\text{[math]}$ ，使得 $\text{[math]}$ ，连结 $\text{[math]}$ ，当 $\text{[math]}$ 于点 $\text{[math]}$ 时，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题